Задание 8. МКТ, термодинамика. ЕГЭ 2026 по физике
Средний процент выполнения: 74%
Ответом к заданию 8 по физике может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 8:
- Определи, какой тепловой процесс или термодинамическая система рассматривается в задании.
- Выдели физические величины, характеризующие тепловой процесс: количество теплоты, работу, внутреннюю энергию.
- Установи, какие из этих величин заданы, а какие подлежат определению или анализу.
- Соотнеси описанный процесс с первым законом термодинамики или с принципами работы тепловых машин.
- Запиши применимые соотношения или законы в общем виде с использованием физических величин.
- Примени записанные законы для анализа процесса или выполнения требуемых вычислений.
- Проверь, что полученный результат согласуется с физическим смыслом термодинамических величин и процессов.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
В цилиндре под поршнем находится гелий (одноатомный газ). Газ расширился при постоянном давлении, совершив работу 3 кДж. Какое количество теплоты сообщили газу? Ответ выразите в (кДж).
Решение
Дано:
$A=3·10^3$Дж
$i=3$
$Q-?$
Решение:
Запишем I начало термодинамики для изобарного процесса (p=const): $Q=A+∆U$(1), где $A=p∆V$(2), $∆U={i}/{2}vR∆T$(3) - изменения внутренней энергии гелия. Исходя из уравнения Менделеева-Клайперона: $p∆V=vR∆T$(4), $∆U={i}/{2}p∆V={i}/{2}A$(5). Подставим (5) в (1): $Q=A+{i}/{2}A=A(1+{i}/{2})=A(1+{3}/{2})=5/2A$(6). Подставим числовые значения в (6): $Q=5/2·3·10^3=7.5кДж$
Задача 2
Какова внутренняя энергия гелия, заполняющего аэростат объёмом 60 м3 при давлении 100 кПа? Ответ выразите в (МДж).
Решение
Дано:
$V=60м^3$
$p=10^5$Па
$i=3$
$U-?$
Решение:
Внутренняя энергия определяется выражением: $U={i}/{2}vRT$(1), где $i=3$ - число степеней свободы у одноатомного газа (гелий - одноатомный газ).
Из уравнения Менделеева-Клайперона имеем: $pV=vRT$(2). Подставим (2) в (1), получим: $U={i}/{2}pV$(3). Подставим числовые значения в (3): $U={3}/{2}·10^5·60=9·10^6=9$МДж.
Задача 3
Тепловая машина с КПД 60% за цикл работы отдаёт холодильнику 100 Дж теплоты. Какое количество теплоты за цикл получает машина от нагревателя? Ответ выразите в (Дж).
Решение
Дано:
$η=60%$
$Q_x=100$Дж
$Q_н-?$
Решение:
1) Из теории о тепловых машинах $η={Q_н-Q_x}/{Q_н}·100%$.
$100=Q_н·0.4$
$0.6=1-{100}/{Q_н}$
$Q_н=250$Дж
Задача 4
В сосуде с подвижным поршнем находятся вода и её насыщенный пар. Если одновременно увеличить в 2 раза температуру сосуда и его объём, то как увеличится его давление? В ответ запишите: примерно в _ раз(а).
Решение
Объём сосуда не влияет на давление насыщенного пара. Влияние температуры на давление насыщенного пара можно определить по уравнению Менделеева-Клайперона $pV=υRT$. Если температуру увеличить в 2 раза, то и давление увеличится в 2 раза.
Задача 5
При изобарном расширении идеальный двухатомный газ получил количество теплоты, равное 800 Дж. Насколько увеличилась внутренняя энергия газа при этом процессе? Ответ выразите в (Дж) и округлите до целых.
Решение
Дано:
$P=const$
$Q=800$Дж
$∆U-?$
Решение:
$∆Q=∆U+A$.
$∆Q=∆U+{2}/{5}·{∆U}⇒∆U={5}/{7}·800=571$ Дж.
Задача 6
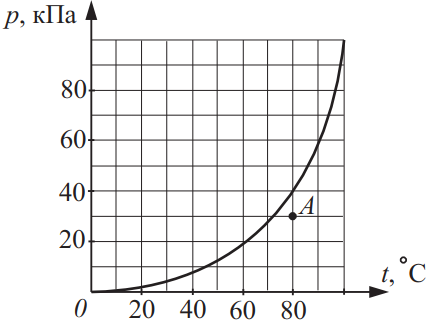
На рисунке изображена зависимость давления p насыщенного водяного пара от температуры t. Точкой A на этом графике обозначено состояние пара, находящегося в закрытом сосуде. Чему равна относительная влажность воздуха в этом сосуде? Ответ выразите в (%).
Решение
При $t=80°C$ $p_н=40$кПа
Относительная влажность воздуха может быть вычислена как отношение давления пара к давлению насыщенного пара при той же температуре: $ϕ={p}/{p_н}·100%={30}/{40}·100%=75%$
Задача 7
Относительная влажность воздуха при температуре 100◦С составляет 60%. Чему равно парциальное давление водяных паров, содержащихся в воздухе? Ответ выразить в (кПа).
Решение
Дано:
$T=100°C$
$ϕ_{от}=60%$
$P_{вп}-?$
Решение:
Известно, что для $T=100°C$ давление насыщенного пара $P_*=100$кПа. Тогда $ϕ={P_{вп}}/{P_*}·100⇒P_{вп}=0.6·100=60$кПа.
Задача 8
У работающего по циклу Карно теплового двигателя температура нагревателя 400 К, а температура холодильника 150 К. Найдите коэффициент полезного действия этого двигателя. Ответ выразите в (%).
Решение
Дано:
$T_н=400K$
$η-?$
$T_x=150K$
Решение:
Для цикла Карно справедливо уравнение $η={T_н-T_x}/{T_н}·100%={400-150}/{400}·100%=62.5%$
Задача 9
Рабочее тело идеальной тепловой машины за один цикл получает от нагревателя теплоту 1000 Дж. Температура нагревателя 500 К, температура холодильника 200 К. Какую работу совершает рабочее тело за один цикл? Ответ выразите в (Дж).
Решение
Дано:
$Q_н=1000$Дж
$T_н=500$К
$T_x=200$К
Решение:
$A=Q_н-Q_x$
$η={T_н-T_x}/{T_н}={Q_н-Q_x}/{Q_н}$ по формуле из основы теплообмена.
$A={(T_н-T_x)Q_н}/{T_н}={300·1000}/{500}=600$Дж.
Задача 10
КПД идеального двигателя внутреннего сгорания равен 60%. Определите температуру в камере сгорания двигателя, если температура струи, выходящей из его сопла, составляет 727◦С. Ответ выразить в (K).
Решение
Дано:
$η=0.6$
$T_{вых}=727+273=1000К$
$T_н-?$
Решение:
$η={T_н-T_x}/{T_н}$ для тепловой машины определяем $T_н$.
$0.6={T_н-1000}/{T_н}; T_н={1000}/{0.4}=2500K$.
Задача 11
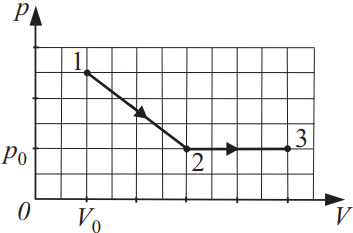
На рисунке показана зависимость давления идеального газа от его объёма при переходе из состояния 1 в состояние 2, а затем в состояние 3. Найдите, чему равно отношение работ газа ${A_{12}}/{A_{23}}$.
Решение
Дано:
${A_{12}}/{A_{23}}-?$
Решение:
Чтобы найти работу газа, нужно посчитать площадь под графиком в координатах p(V).
Посчитаем площадь под графиком в процессе 1-2 (как площадь трапеции) $$A_{12}={p_{0}+2,5p_{0}}/{2}(3V_{0}-V_{0})=3,5 p_{0}V_{0}$$
Посчитаем работу газа в процессе 2-3 $$A_{23}=p_{0}(5V_{0}-3V_{0})=2 p_{0}V_{0}$$
Итого: $${A_{12}}/{A_{23}}={3,5 p_{0}V_{0}}/{2 p_{0}V_{0}}=1,75$$
Задача 12
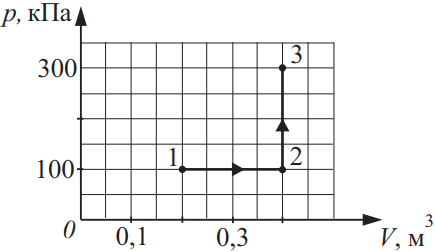
На pV -диаграмме представлен процесс изменения состояния идеального одноатомного газа. Масса газа не меняется. Какую работу совершает газ при переходе из состояния 1 в состояние 3? Ответ выразить в (кДж).
Решение
Дано:
$T=const$
$m=const$
$A_{1-3}-?$
Решение:
Из условия: $A_{13}=A_{12}+A_{23}$, т.к. при 2-3 $∆V=0; ∆A=p∆V$, то и работа $A_{23}=0$, тогда $A_{13}=A_{12}=p∆V=100·0.2=20$кДж.
Задача 13
В кубическом метре воздуха в помещении при температуре 18◦С находится 1,31 · 10−2 кг водяных паров. Пользуясь таблицей плотности насыщенных паров воды, определите относительную влажность воздуха. Ответ выразите в (%). Ответ округлите до целого.
| t, ◦ C | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| ρ, г/м3 | 13,6 | 14,5 | 15,4 | 16,3 | 17,3 | 18,3 | 19,4 | 20,6 | 21,8 |
Решение
Дано:
$V=1м^3$
$T=18°C$
$m_{вп}=1.31·10^{-2}$кг
$ϕ_{отн}-?$
Решение:
1) Определим плотность водяных паров в комнате $ρ_{вп}={m_{вп}}/{V}={1.31·10^{-2}}/{1}{кг}/{м^3}$.
2) Используя таблицу, определим, и по при температуре 18°C плотность насыщенных паров равна $ρ_{нп}=1.54·10^{-2}{кг}/{м^3}$.
3) Тогда относительная влажность воздуха в комнате равна $ϕ_{отн}={ρ_{вп}}/{ρ_{нп}}·100%={1.31·10^{-2}}/{1.54·10^{-2}}≈85%$.
Задача 14
Определите мощность кипятильника, который за 5 минут нагревает 210 г воды от 14◦C до температуры кипения. Потерю энергии не учитывать. Ответ выразите в (Вт) и округлите до целых.
Решение
Дано:
$t=5=5·60=300$c
$m=0.21$кг
$t_1=14°C$
$t_2=100°C$
$N-?$
Решение:
Мощность по определению равна: $N={A}/{t}={Q}/{t}={cm(t_-t_1)}/{t}$(1), где $m$ - масса воды, $c$ - удельная теплоемкость воды $c=4200$Дж/кг·°C. Подставим числовые значения в (1), имеем: $N={4200·0.21·(100-14)}/{300}=252.84$Bт. После округления до целых: 253 Вт
Задача 15
Газ, находящийся в теплоизолированном цилиндре с подвижным поршнем, получает от нагревателя количество теплоты, равное 200 Дж. Поршень при этом, преодолевая сопротивление 800 Н, переместился на 10 см. Насколько изменилась внутренняя энергия газа? В ответе запишите на сколько (Дж).
Решение
Дано:
$Q=200$Дж
$F=800$Н
$∆x=0.1$м
$∆U-?$
Решение:
Запишем I начало термодинамики: $Q=A+∆U$(1), где $A=F·∆x$(2) - работа газа, $∆U$ - изменение внутренней энергии газа. Тогда из (1) с учетом (2) имеем: $∆U=Q-A=Q-F·∆x=200-800·0.1=200-80=120$Дж.
Задача 16
В цилиндре под поршнем находится 2 кг воздуха (молярная масса μ = 0,029 кг/моль) при 20◦С под давлением 1 МПа. Чему равна работа при изобарном нагревании воздуха до 100◦С? Ответ выразите в (кДж), округлив до десятых.
Решение
Дано:
$m=2$кг
$μ=0.029$кг/моль
$t_1=20°C$
$t_2=100°C$
$p=10^6$Па
$R=8.31$Дж/моль·К
$A-?$
Решение:
Работа в изобарном процессе определяется выражением: $A=p·∆V$(1), где $p$ - давление, $∆V$ - изменение объема.
Запишем уравнение Менделеева-Клайперона: $p∆V={m}/{μ}R∆T$(2), учитывая, что $∆T=∆t=t_2-t_1=100°C-20°C=80K$ (изменение температуры в °C и в К имеет одинаковое значение).
Подставим (2) в (1), получим: $A=p·∆V={m}/{μ}R∆T={2·8.31·80}/{0.029}=45848.275=45.8$кДж.
Задача 17
Определите КПД нагревателя, расходующего 80 г керосина на нагревание 3 л воды на 90 К. Удельная теплота сгорания керосина 4,3·107 Дж/кг. Ответ выразите в (%) и округлите до целых.
Решение
Дано:
$m_к=0.08$кг
$V_в=3=3·10^{-3}м^3$
$ρ_в=1000{кг}/{м^3}$
$∆T=90K$
$q=4.3·10^7$Дж/кг
$c=4200$Дж/кг·К
$η-?$
Решение:
КПД нагревателя определяется выражением: $η={A_{полез}}/{A_{затр}}·100%$(1), $m_в=ρ_в·V_в$(2) - масса воды, где $A_{полез}=Q_п=cm_в·∆T=c·ρ_в·V_в·∆T$(3) - полезная работа; $A_{затр}=Q_з=q·m_к$(4) - затраченная (полезная) работа. Подставим (3) и (4) в (1) получим: $η={c·ρ_в·V_в·∆T}/{q·m_к}·100%={4200·10^3·3·10^{-3}·90}/{4.3·10^7·8·10^{-2}}·100%={1134000}/{3440000}·100%=32.965%=33%$.
Задача 18
Относительная влажность воздуха 65%, давление насыщенного пара в нём при некоторой температуре равно 3,4 кПа. Чему равно парциальное давление пара при этой же температуре? Ответ выразите в (кПа), округлив до сотых.
Решение
Дано:
$ϕ=65%$
$p_0=3.4·10^3$Па
$p-?$
Решение:
По определению относительная влажность воздуха равна: $ϕ={p}/{p_0}·100%$(1), где $p$ - парциальное давление пара. Из (1) найдем $p$: $p={ϕ·p_0}/{100%}$(2). Подставим числа: $p={65·3.4·10^3}/{100%}=2210=2.21$кПа.
Задача 19
Тепловая машина имеет КПД 25%. Найдите среднюю мощность передачи теплоты холодильнику, если рабочее тело машины за 10 с получает от нагревателя 30 кДж теплоты. Ответ выразите в (кВт).
Решение
Дано:
$η=0.25$
$t=10c$
$Q_н=30$кДж
$P_x-?$
Решение:
$P_н={Q_н}/{t}={30}/{10}=3$кВт.
$η={P_н-P_x}/{P_н}·100$.
$P_x=P_н-η·P_н=3-0.75=2.25$кВт.
Задача 20
Аргону сообщили 30 кДж теплоты, и он изобарно расширился. При этом объём газа увеличился на 0,6 м3. Каково давление газа? Ответ выразите в (кПа).
Решение
Дано:
$p=const$
$Q=30·10^3Дж$
$∆V=0.6м^3$
$p-?$
Решение:
Запишем I начало термодинамики для изобарного процесса: $Q=A+∆U$(1), где $A=p·∆V$(2) - работа газа; $∆U={i}/{2}υR∆T$(3) - изменение внутренней энергии газа. Поскольку аргон-газ одноатомный, то число степеней свободы $i=3$.
Запишем уравнение Менделеева-Клайперона: $p·∆V=υR∆T$(4), тогда $∆U={3}/{2}p·∆V$(5)
Подставим (2) и (5) в (1): $Q=A+∆U=p·∆V+{3}/{2}p·∆V={5}/{2}p∆V$(6), откуда $p={2Q}/{5∆V}={2·30·10^3}/{5·0.6}=20·10^3=20кПа$
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ







