Задание 24. Молекулярная физика. Термодинамика. Расчетная задача высокого уровня. ЕГЭ 2026 по физике
Средний процент выполнения: 23.8%
Ответом к заданию 24 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
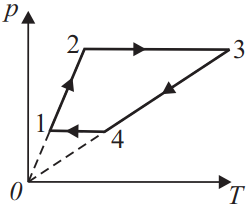
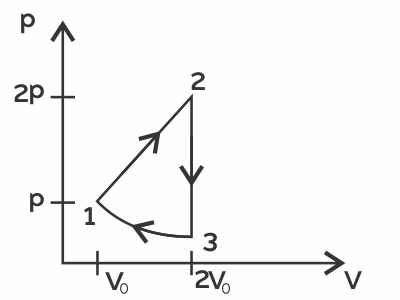
С ν = 3 молями идеального газа совершён цикл, изображённый на рисунке. Температуры газа в различных состояниях равны: T1 = 400 K, T2 = 800 K, T3 = 2400 K, T4 = 1200 K. Найдите работу газа за цикл.
Решение
1) Из рисунка видно, что на участках 1-2 и 3-4 процесс изохорный, т.е. $V_1=V_2$ и $V_3=V_4$, поэтому $A_{1-2}$ и $A_{3-4}=0$.
2) Тогда для $A_{23}=p_2(V_3-V_2)$, а $A_{41}=p_1(V_1-V_4)$. (учтено, что процессы 2-3 и 4-1 изобарные, т.е. $p_2=p_3$, $p_1=p_4$
3)Работа газа за цикл: $A=p_2(V_3-V_2)+p_1(V_1-V_4)$.
4) По закону Менделеева-Клайперона $\{\table\p_1V_1=νRT_1; \p_1V_4=νRT_4; \p_2V_2=νRT_2; \p_2V_3=νRT_3;$ подставим в (3) получим (5).
5) $A=νR(T_3-T_2+T_1-T_4)=19944$Дж.
Задача 2
Шарик массой 0,5 кг, падая с некоторой высоты, ударяется о наклонную плоскость и упруго отскакивает от неё без потери скорости. Угол наклона плоскости к горизонту 30◦. За время удара плоскость получает импульс 2 кг·м/c. Определите, на какую высоту (относительно точки отскока) поднимется тело. Ответ выразите в см.
Решение
Решение:
По закону сохранения энергии $F∆t=m∆υ$, где $∆υ=υ_1·cosα-(-υ_2·cosα)⇒∆υ=cosα(υ_1+υ_2); υ_1=υ_2=υ$. Тогда $F∆t-2·m·υ·cosα$. Из условия $υ_y=υ·sin({π}/{2}-2·α)-g·t=υ·cos2α-gt; υ_y=0$ в верхней точке, следовательно, $t={υ·cos2α}/{g}$, а $H={υ^2·sin^2α}/{2g}; υ={F∆t}/{2m·cosα}$, тогда $H={({4}/{2·0.5·{√3}/{2}})·0.5^2}/{2·10}=6.7$см
Задача 3
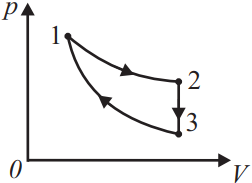
КПД тепловой машины, работающей по циклу, состоящему из изотермы 1–2, изохоры 2–3, адиабаты 3–1, равен η, а разность максимальной и минимальной температуры газа в цикле равна ∆T . Определите работу, совершаемую ν молями одноатомного идеального газа за один цикл в изотермическом процессе.
Решение
Дано: $v$, $η$, $∆T=T_2-T3$ ($T_2=T_1$ - максимальное значение температуры, $T_3$ - минимальное
КПД цикла: $η=1-{|Q_х|}/{Q_н}$ (1).
${Q_х}$ - количество теплоты отданное газом за весь цикл
${Q_н}$ - количество теплоты полученное газом за весь цикл
Пусть $Q_{12}$, $Q_{23}$, $Q_{31}$ - количество теплоты полученное газом в каждом процессе,
$∆U_{12}$, $∆U_{23}$, $∆U_{31}$- изменение внутренней энергии в каждом процессе,
$A_{12}$, $A_{23}$, $A_{31}$ - работа газа в каждом процессе.
Запишем 1 закон термодинамики для процессов 12 и 23:
12 - изотермический: $Q_{12}=∆U_{12}+A_{12} =A_{12}$, т.к. $∆U_{12}=0$ из-за неизменной температуры. Так как в процессе 12 объём увеличивается, $A_{12}$ и $Q_{12}$ $>0$, газ получает тепло.
23 - изохорный: $Q_{23}=∆U_{23}+A_{23} =∆U_{23}$, т.к. $A_{23}=0$ из-за того, что объём не меняется. Так как в процессе 12 объём увеличивается, $∆U_{23}=3/2vR(T_3-T_2)=3/2vR(-∆T)=-3/2vR∆T<0$, значит и $Q_{23}$ $<0$, газ отдаёт тепло.
Процесс 31 - адиабатный, т.е. $Q_{31}=0$. Тогда
${Q_х}= Q_{23}=∆U_{23}=-3/2vR∆T$
${Q_н}= Q_{12}=A_{12}$
Подставим полученные выражения для ${Q_х}$ и ${Q_н}$ в (1):
$η=1-{|-3/2vR∆T|}/{A_{12}}=1-{3/2vR∆T}/{A_{12}}$ $=>$ $A_{12}={3/2vR∆T}/{1-η}$
Задача 4
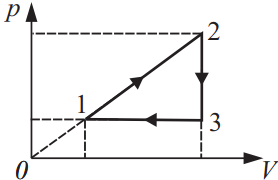
Одноатомный газ участвует в циклическом процессе, представленном на pV -диаграмме. В состоянии 2 его температура в 4 раза выше, чем в состоянии 1. Определите КПД циклического процесса.
Решение
Дано:
$i=3$
$T_2=4T_1$
$η-?$
Решение:
КПД находится как отношение работы за цикл к количеству теплоты, полученной за цикл. В данном случае, теплота получена на участке 1-2. На этом участке давление и объем прямо пропорциональны: ${p_1}/{p_2}={V_1}/{V_2}$
Из уравнения Менделеева-Клайперона: ${p_1V_1}/{T_1}={p_2V_2}/{T_2}$ следует, что $({p_1}/{p_2})^2={T_}/{T_1}$ т.е. ${p_2}/{p_1}={V_2}/{V_1}=√4=2$. $p_2=2p_1, V_2=2V_1$
Работа А за цикл равна: $A={1}/{2}(p_2-p_1)·(V_2-V_1)≈{1}/{2}(p_2V_2-p_1V_1-p_2V_1+p_1V_1)={1}/{2}(2p_1·2V_1-p_1·2V_1-2p_1V_1+p_1V_1)={1}/{2}(4p_1V_1-2p_1V_1-2p_1V_1+p_1V_1)=0.5p_1V_1$
Количество теплоты равно: $Q=A_{1,2}+∆U_{1,2}={p_1+p_2}/{2}·(V_2-V_1)+{3}/{2}(p_2V_2-p_1V_1)={3p_1}/{2}·(2V_1-V_1)+{3}/{2}(2p_1·2V_1-p_1V_1)={3p_1V_1}/{2}+{3·3p_1V_1}/{2}={12}/{2}p_1V_1=6p_1V_1$
Тогда КПД равен: $η={A·100%}/{Q_{пол}}={0.5p_1V_1}/{6p_1V_1}·100%≈8.33%$
Задача 5
Свинцовая пуля массой 10 г, летящая со скоростью 400 м/с, пробивает деревяный шар массой 1 кг, висящий на прочной нити, и вылетает из него со скоростью 300 м/с. Определите увеличение температуры пули после пробивания шара, если на её нагревание идёт 60% потери кинетической энергии системы «пуля–шар». Удельная теплоёмкость свинца $c=140$Дж/кг·С. Ответ выразите в кельвинах и округлите до десятых.
Решение
Дано:
$m_1=10^{-2}$кг
$υ_1=400$м/с
$m_2=1$кг
$υ_2=300$м/с
$c=140$Дж/кг·С
$Q=0.6∆E_к$
$∆T-?$
Решение:
Рассчитаем потери кинетической энергии системы "пуля-шар": $∆E_к={mυ_1^2}/{2}-{mυ_2^2}/{2}={m}/{2}·(υ_1^2-υ_2^2)={10^{-2}}/{2}(16·10^4-9·10^4)={7·10^2}/{2}=350$Дж.
Количество теплоты, которое получает пуля равно: $Q=cm·∆t$(2), где $c$ - удельная теплоемкость свинца, $c=140$Дж/кг·С.
По условию задачи: $Q=0.6·∆E_к$, откуда $∆t={0.6∆E_к}/{cm}$(3). Подставим числовые значения в (3): $∆t={0.6·350}/{10^{-2}·140}=150°C$. Поскольку $1°C=1K$, то $∆t=∆T=150K$
Задача 6
Два моля одноатомного газа, находящегося в цилиндре при температуре 400 К и давлении 4 · 105 Па, расширяются и одновременно охлаждаются так, что его давление в этом процессе обратно пропорционально объёму в кубе (V3). Какую работу совершил газ при расширении, если он отдал количество теплоты 1979 Дж, а его давление стало равным 0,5 · 105 Па? Ответ укажите в кДж.
Решение
Дано:
Q = 1979 Дж,
pк = 0,5 · 105 Па,
p0 = 4 · 105 Па,
T0 = 400 K,
A = ?
Решение:
p = α/V3 => V = α/∛p
По закону Менделеева-Клайперона:
pV = νRT
(p0 α) / (3p0) = νRT0
(pк α) / (3pк) = νRTк
Tк = T0 (p0/pк)1/3 = 400 (0.5/4)1/3 = 100 K
A = -Q - ∆U = -1979 - (3/2) · 2 · 8,31 · (100 - 400) = 5,5 кДж
Задача 7
За один цикл идеальная тепловая машина совершает работу, составляющую 25 кДж. При изотермическом сжатии работа внешних сил равна 20 кДж. Определите отношение температуры нагревателя к температуре холодильника.
Решение
Дано:
$A=25·10^3Дж$
$A′=20·10^3Дж$
${T_н}/{T_х}-?$
Решение:
КПД идеальной тепловой машины определяется выражением: $η={T_н-T_х}/{T_н}=1-{T_х}/{T_н}$(1), откуда ${T_x}/{T_н}=1-η$(2).
С другой стороны: $η={Q_н-|Q_x|}/{Q_н}={A}/{Q_н}$(3).
При изотермическом сжатии работа внешних сил равна 20кДж, значит, в этом процессе газ отдает тепло холодильнику. Согласно 1 закону термодинамики $Q_х=-A'+0$ и значит, $A′=|Q_x|$. Тогда найдем $Q_н$ - количество теплоты, полученное от нагревателя: $Q_н=A+|Q_x|=A+A′=25+20=45кДж.$
По формуле (3) найдем КПД $η$: $η={A}/{Q_н}={25·10^3}/{45·10^3}=0.55$(5)
Подставим числовые значения в (2) и найдем ${T_н}/{T_х}$:
${T_х}/{T_н}=1-0.555=0.444$
${T_н}/{T_х}={1}/{0.444}$
${T_н}/{T_х}=2.25$
Задача 8
Для приготовления ванны при температуре 40◦С используется водонагреватель, который даёт воду, нагретую до температуры 65◦С. Температура воды в водопроводе составляет 15◦С. Каков объём ванны, если для её приготовления используется 135 л воды из водопровода?
Решение
Дано:
$V_x=135$л
$t=40°C$
$t_1=65°C$
$t_2=15°C$
$V-?$
Решение:
Объем ванны равен сумме объемов холодной воды из водопровода $V_x$ и горячей воды из водонагревателя $V_г$: $V=V_x+V_г$(1)
При смешивании горячей и холодной воды происходит теплообмен между двумя системами: горячая вода отдает часть своей энергии холодной воде, а холодная вода принимает эту энергию: $Q_г=Q_x$(2)
Учитывая, что масса воды $m=ρ·V$(3), $V$ - объем воды; $ρ$ - плотность воды, $c$ - удельная теплоемкость воды:
$Q_г=cm_г(t_1-t)=cρV_г(t_1-t)$ - количество теплоты, которое отдает горячая вода;
$Q_х=cm_х(t-t_2)=cρV_х(t-t_2)$ - количество теплоты, которое принимает холодная вода;.
$cρV_г(t_1-t)=cρV_x(t-t_2)$
$25V_г=25V_ч⇒V_г=V_х$
Получается, что объем горячей и холодной воды одинаковы. Учитывая, что объем ванны: $V=V_x+V_г=135+135=270$л.
Задача 9
Кусок свинца массой 2 кг нагрели, сообщив ему 110 кДж теплоты. Свинец расплавился на 50% своей массы. Какова была начальная температура свинца? Температура плавления свинца 600 К, удельная теплоёмкость свинца 130 Дж/(кг·К)
Решение
Дано:
$m=2$кг
$Q=110·10^3$Дж
$λ=0.25·10^5$Дж/кг
$m_2=0.5m$
$T_2=600K$
$c=130$Дж/кг·К
$T_1-?$
Решение:
Общее количество теплоты, которое сообщили свинцу массой $m$ равно: $Q=Q_1+Q_2$ (1),
где $Q_1=cm(T_2-T_1)$ (2) - количество теплоты, которое сообщили свинцу до температуры плавления $T_2$.
$Q_2=m_2·λ=0.5m·λ$ (3) - количество теплоты, затраченное на плавление с учетом того, что расплавилось лишь 0,5 массы свинца.
$λ$ - удельная теплота плавления свинца, $c$ - удельная теплоемкость свинца.
Подставим (2) и (3) в (1): $Q=cmT_2-cmT_1+0.5mλ$, откуда найдем температуру $T_1$:
$cmT_1=cmT_2+0.5mλ-Q; T_1={cmT_2+0.5mλ-Q}/{cm}$(4).
Подставим числовые значения в (4):
$T_1={130·2·600+0.5·2·0.25·10^5-110·10^3}/{130·2}={156000+25000-110000}/{260}={71000}/{260}=273K$ (или 0°C).
Задача 10
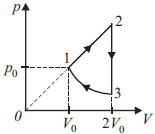
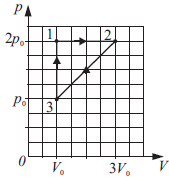
Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу $A_{12} = 1000$ Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу $|A_{31}| = 370$ Дж. Количество вещества газа в ходе процесса не меняется. Найдите КПД цикла.
Решение
Дано:
$a_{12}=1000$Дж
$|A_{31}|=370$Дж
$ν=const$
$η-?$
Решение:
Участок 1-2 - прямая, выходящая из начала координат, следовательно, $p_2=2p_0$
Запишем 1-е е-начало термодинамики: $Q_{12}=A_{12}+∆U_{12} > 0$
$Q_{23}=∆U_{23} < 0$
$Q_{31}=A_{31}+∆U_{31} = 0$(адиабата)
По определению: $η={A}/{Q_+}; Q_+=Q_{12}; A=A_{12}-|A_{31}|$
$A_{12}$ - площадь трапеции:
$A_{12}={(p_0+2p_0)}/{2}V_0={3}/{2}p_0V_0⇒p_0V_0={2}/{3}A_{12}$
$∆U_{12}={3}/{2}νR∆T={3}/{2}∆(pV)={3}/{2}(4p_0V_0-p_0V_0)={9}/{2}p_0V_0$
$∆U_{12}=3A_{12}⇒Q_{12}=4A_{12}$
$η={A_{12}-|A_{31}|}/{4A_{12}}≈0.158$
Задача 11
Одноатомный идеальный газ совершает циклический процесс, показанный на рис.. Масса газа постоянна. За цикл от нагревателя газ получает количество теплоты $Q_н = 10$ кДж. Чему равна работа газа за цикл? Ответ округлите до целых.
Решение
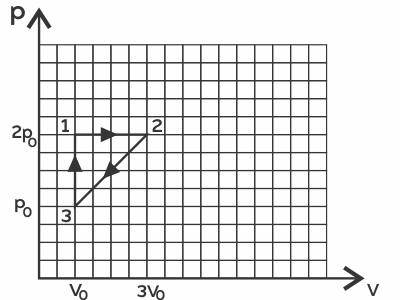
Запишем 1 закон термодинамики для каждого участка цикла и проанализируем, на каких участках газ получает теплоту:
$Q_12=∆U_{12}+A_{12}$,
$A_12=2p_0(V_2-V_1)=2p_0(3V_0-V_0)=4p_0V_0>0$ ,
$∆U_{12}=3/2(p_2V_2-p_1V_1)=3/2(2p_03V_0-2p_0V_0)=3/2·4p_0V_0>0$
Значит $Q_12>0$, газ получает тепло
$Q_23=∆U_{23}+A_{23}$,
$A_23<0$ т.к. $V_3 < V_0$,
$∆U_{23}=3/2(p_3V_3-p_2V_2)=3/2(p_0V_0-2p_03V_0)=-3/2·5p_0V_0<0$
Значит $Q_23<0$, газ отдаёт тепло
$Q_31=∆U_{31}+A_{31}$,
$A_31=0$ т.к. $V_3=V_1$,
$∆U_{31}=3/2(p_1V_1-p_3V_3)=3/2(2p_0V_0-p_0V_0)=3/2p_0V_0>0$
Значит $Q_31>0$, газ получает тепло
Таким образом, теплота, полученная от нагревателя: $Q_н=Q_{12}+Q_{31}=∆U_{12}+A_{12}+∆U_{31}+A_{31}=3/2·4p_0V_0+4p_0V_0+3/2p_0V_0+0={23}/{2}p_0V_0$
Значит $p_0V_0=2/{23} Q_н$
Работу газа за цикл найдём как площадь, ограниченную этим циклом на графике $pV$:
$A=1/2(2p_0-p_0)·(3V_0-V_0)=p_0V_0={2}/{23}Q_н≈870$Дж
Задача 12
В закрытом сосуде находится одноатомный идеальный газ при нормальных условиях, масса которого равна 2 г. После охлаждения газа его давление уменьшилось на 50 кПа. Какова молярная масса газа, если отданное им количество теплоты равно 170,2 Дж? (Нормальные условия: $10^5$Па, $273$K )
Решение
$m=2г, p_1=10^5$Па, $T_1=273$K
$p_2=p1-50$кПа$=50$кПа, $Q=170.2$Дж
Первый закон термодинамики: $Q=A+∆U$. $A=0$, т.к. сосуд закрыт и объём $V=const$. Тогда $Q=∆U={3}/{2}{m}/{μ}R(T_2-T_1)$
Т.к. процесс протекает при постоянном объёме, то выполняется закон ${p_1}/{T_1}={p_2}/{T_2}=const⇒T_2={p_2}/{p_1}T_1={T_1}/{2}$
Тогда $Q={3}/{2}{m}/{μ}R({T_1}/{2}-T_1)={3mRT_1}/{4μ}⇒μ={3mRT_1}/{4Q}={3·0.002·8,31·273}/{4·170,2}=0,0199$ кг/моль$≈20$ г/моль
Задача 13
Какая доля подводимой к одноатомному идеальному газу теплоты в изобарическом процессе расходуется на работу газа?
Решение
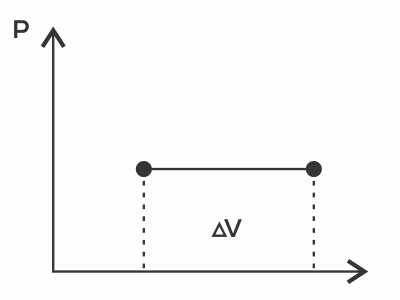
Работа в изобарическом процессе $A=p∆V$
Изменение внутренней энергии $∆U={3}/{2}p∆V$
$Q=A+∆U={5}/{2}p∆V$
${A}/{Q}={2}/{5}=0.4$
Задача 14
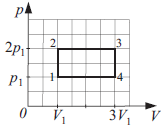
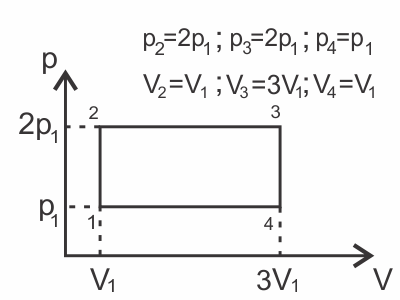
Найдите КПД цикла, изображённого на рисунке для идеального одноатомного газа.
Решение
$η={A_0}/{Q_{подв}}$
$A_0$ - работа газа за цикл, $Q_{подв}$ - тепло, подведенное к газу.
$A_0$ - численно равна площади внутри графика $A_0=p_1·2V_1$
$Q_{подв}=Q_{12}+Q_{23}; Q_{12}=∆U_{12}={3}/{2}(p_2V_2-p_1V_1)={3}/{2}p_1V_1$
$Q_{23}=A_{23}+∆U_{23}=2p_1(3V_1-V_1)+{3}/{2}2p_1(3V_1-V_1)=10p_1V_1$
$η={A_0}/{Q_{подв}}={2p_1V_1}/{{3}/{2}p_1V_1+10p_1V_1}={4}/{23}≈0.17$
Можно выразить в процентах $η=17%$, т.к. в условии это не уточняется
Задача 15
Свинцовая пуля ударяется о железную плиту и отскакивает от неё. На нагревание пули идёт 75% потерянной ею механической энергии. Температура пули перед ударом t1 = 40$°$С. Какая часть пули расплавилась при ударе, если известно, что скорость пули перед ударом о плиту v1 = 350 м/с, а после удара v2 = 100 м/с? Температура плавления свинца 327,5$°$C, удельная теплота плавление $λ=2.5·10^4$, удельная теплоёмкость $c=130$ Дж/(кг·К). Ответ представьте в процентах.
Решение
Пусть $m$ - масса пули, $∆E$ - изменение энергии пули.
$|∆E|={mv_1^2}/{2}-{mv_2^2}/{2}$
$Q={3}/{4}|∆E|$ - тепло, перешедшее в тепло. Пусть $α$-часть пули, которая расплавилась $Q=mc∆t+αmλ, ∆t=(327.5-40)°C=287.5°C$
${3}/{4}{m}/{2}(v_1^2-v_2^2)=m(c∆t+αλ), λ=2.5·10^4$
$α={{3}/{8}(v_1^2-v_2^2)-c∆t}/{λ}=19.25·10^{-2}$
$α=19.25%$
Задача 16
В комнате размерами $2,\!5×4×5$ м при $t_0 = 25°$C влажность воздуха составляет $85%$. Какова масса росы, которая может выпасть при уменьшении температуры до $t_1 = 10°$C? (Давление насыщенного водяного пара при $25°$C $p_{{25°}C} = 3,\!17⋅10^3$ Па, при $10°$C $p_{{10°}C} = 1,\!23⋅10^3$ Па.) Ответ укажите в граммах.
Решение
1 способ
1) Парциальное давление пара при температуре 25°C определим через влажность: $p_{0} = {ϕ} / {100%}⋅p_{{25°}C} = 0,85 ⋅ 3,17 ⋅ 10^3 = 2,\!6945⋅10^{3}$ Па.
Изначальное давление водяного пара $p_{0}$ больше, чем давление насыщенного пара при температуре 10°C $p_{1}$, значит при понижении температуры весь лишний водяной пар выделится в виде росы, а давление пара при температуре 10°C будет равно давлению насыщенного пара при этой температуре: $p_{1}=p_{{10°}C}$
2) Чтобы определить массу росы, вычислим массу водяного пара в комнате $m_0$ при температуре 25 °C и $m_1$ при температуре 10 °C.
Из уравнения Менделеева Клапейрона: $p_0 V = {m_0} / {M}RT_0$ $ ⇒$ $ m_0 = {p_0 VM}/{RT_0}$, аналогично $ m_1 = {p_1 VM}/{RT_1}$
где $T_0=t_0+273$, $T_1=t_1+273$ - абсолютные температуры, M - молярная масса воздуха, V = 2,5×4×5=50 м$^3$ - объём комнаты
3) Масса росы равна разнице масс паров:
$m=m_0-m_1= {p_0 VM}/{RT_0}-{p_1 VM}/{RT_1}={VM}/R ⋅({p_0}/{T_0}-{p_1}/{T_1})={VM}/R ⋅({p_0}/{t_0+273}-{p_{{10°}}/{t_1+273})={50 ⋅18⋅10^{-3}}/{8,\!31}⋅({2,\!6945⋅10^{3}}/{25+273}-{1,\!23⋅10^3}/{10+273})≈508⋅10^{-3}$ кг = 508 г.
2 способ
1) Используя уравнение Менделеева-Клапейрона, найдём плотность насыщенного водяного пара при $25°$C и $10°$C:
$ρ V = {m} / {M}RT ⇒ p = {ρ} / {M}RT ⇒ ρ = {pM} / {RT}.$
$ρ_{{25°}C} = {p_{{25°}C}⋅ M_{H_2O}} / {RT} = {3,\!17⋅10^3⋅18⋅10^{-3}} / {8,\!31⋅298} = 23⋅10^{-3}$ кг/м$^3$.
$ρ_{{10°}C} = {1,\!23⋅10^3⋅18⋅10^{-3}} / {8,\!31⋅283} = 9,\!4⋅10^{-3}$ кг/м$^3$.
2) По относительной влажности при $25°$C найдём парциальную плотность водяного пара в помещении: $ρ = {ϕ} / {100%}⋅ρ_{{25°}C} = 19,\!55⋅10^{-3}$ кг/м$^3$.
3) При понижении температуры влажность увеличивается до $100%$, избыток водяного пара конденсируется таким образом, что его плотность остаётся равной плотности насыщенного пара.
4) Масса пара, превратившаяся в жидкость, $δ m = (ρ - ρ_{{10°}C})V = 10,\!15⋅10^{-3}⋅50 = 507,5⋅10^{-3}$кг = 507,5 г.
Задача 17
Горизонтальная поверхность разделена на две части: гладкую и шероховатую. На шероховатой поверхности на границе этих частей находится брусок массой $100$ г. Со стороны гладкой части на него по горизонтали налетает металлический шар массой $0,\!5$ кг, движущийся со скоростью $2$ м/с. Определите расстояние (в метрах), которое пройдёт кубик до остановки после абсолютно упругого центрального соударения с шаром, если коэффициент трения кубика о поверхность $0,\!2$.
Решение
Дано:
$m=0,1кг$
$M=0,5кг$
$v_0=2м/с$
$μ=0,2$
$S-?$
Решение:
Так как удар был абсолютно упругим, то запишем закон сохранения механической энергии (ЗСЭ) и закон сохранения импульса (ЗСИ) для шара и бруска:
ЗСИ в проекции на горизонтальную ось:
$$Mv_0=Mv_1+mv_2$$
где v_1, v_2 - скорость шара и бруска сразу после соударения соответственно. Запишем ЗСЭ:
$${Mv_0^2}/{2}={Mv_1^2}/{2}+{mv_2^2}/{2}$$
Откуда получаем, что: $v_2={2Mv_0}/{M+m}$
Запишем закон изменения механической энергии для движения по шероховатой поверхности: $$ ΔE_{кин} = A_тр ⇒ {mv_2^2}/{2}=F_тр S=μ mgS$$ откуда получаем: $S={1}/{2μg}({2Mv_0}/{M+m})^2=2.8 м$
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

