Задание 23. Молекулярная физика. Термодинамика. Электродинамика. Оптика. Расчетная задача. ЕГЭ 2026 по физике
Средний процент выполнения: 33.7%
Ответом к заданию 23 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
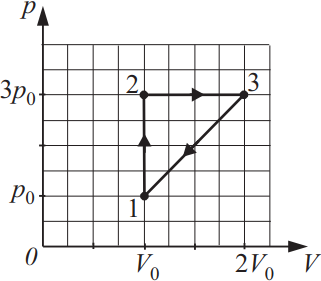
Идеальный газ в количестве 5 моль совершает циклический процесс, изображённый на pV -диаграмме. p0 = 105 Па, V0 = 2 л. Чему равна работа цикла? Ответ выразите в (Дж).
Решение
Дано:
$p_0=10^5$Па
$v=5$ моль
$V_0=2л=2·10^{-3}м^3$
$A-?$
Решение:
Работа цикла А равна площади, ограниченной циклом на графике pV: $A={1}/{2}·(3p_0-p_0)·(2V_0-V_0)={1}/{2}·2p_0·V_0=p_0V_0=10^5·2·10^{-3}=200$Дж.
Задача 2
Идеальная тепловая машина работает по циклу Карно, при этом 85 % количества теплоты, получаемого от нагревателя, передаётся холодильнику. Машина получает от нагревателя количество теплоты 5,4 кДж. Найдите работу, совершаемую за один цикл. Ответ выразите в (Дж).
Решение
Дано:
$Q_2=0.85Q_1$
$Q_н=5.4$Дж
$А-?$
Решение:
КПД тепловой машины: $η={Q_1-Q_2}/{Q_1}={0.15Q_1}/{Q_1}=0.15$.
$A=η·Q_н=0.15·5.4·10^3=810$Дж.
Задача 3
В комнате размером V = 10 × 5 × 3 м3 поддерживается температура T1 = 373 K, давление сухого воздуха равно 200кПа, а водяного пара 80кПа. Определите относительную влажность воздуха.
Решение
Дано:
$V=10·5·3м^3$
$T_1=373K$
$ϕ_{отн}$ ?
Решение:
При $T=373К$ пар Pнасыщ. = 100кПа => относительная влажность $ϕ_{отн}$ = $P/P_{н}$*100% = $80/100$ *100% = 80%
Задача 4
Газ в сосуде находится под давлением 300 кПа при температуре 227◦C. Определите давление газа после того, как половина массы газа выпущена из сосуда, а температура понижена на 80◦C.
Решение
Дано:
$p_1=300·10^3$Па
$t_1=227°C$
$m_1=m$
$m_2={m}/{2}$
$∆T=80°C$
$V_1=V_2=V=const$
$R=8.31$Дж/моль·К
$p_2-?$
Решение:
Найдем абсолютную температуру $T_1$: $T_1=273+t_1=273+227=500K$, тогда $T_2=T_1-∆T=500-80=420K$,
Из уравнения Менделеева-Клайперона имеем:
$p_1·V={m}/{μ}RT_1$(1),
$p_2·V={{m}/{2}RT_2}/{μ}$(2), где $R$ - универсальная газовая постояннаяm, $μ$ - молярная масса газа. Разделим выражение (2) на (1): ${p_2·V}/{p_1·V}={{m}/{2}RT_2}/{μ}·{μ}/{mRT_1}⇒p_2={0.5T_2·p_1}/{T_1}$(3). Подставим числовые значения в (3): $p_2={0.5·420·300·10^3}/{500}=126·10^3=126$кПа.
Задача 5
Предмет высотой 15 см помещён на расстоянии 1,5F от собирающей линзы. Определите, какой высоты получится на экране изображение предмета, если оно перпендикулярно к главной оптической оси. Ответ выразите в (м).
Решение
Дано:
$d=1.5F$
$H=0.15$м
$h-?$
Решение:
Запишем уравнение тонкой линзы: ${1}/{F}={1}/{d}+{1}/{f}$(1), где $f$ - расстояние от линзы до изображения, $d$ - расстояние от предмета до линзы.${1}/{f}={1}/{F}-{1}/{1.5F}={1.5-1}/{1.5F}={1}/{3F}$ или $f=3F$(2)
Увеличение линзы $Г={f}/{d}={3F}/{1.5F}=2$(3).
Тогда высота изображения: $h=Г·H=2·0.15=0.3$м.
Задача 6
Какая масса воздуха выйдет из комнаты, если температура воздуха возросла с 10◦С до 20◦С? Объём комнаты 60 м3, давление нормальное. Ответ округлите до десятых. Ответ выразите в (кг).
Решение
Дано:
$T_1=10°C$
$T_2=20°C$
$V=60м^3$
$P=P_{ном}$
$∆m-?$
Решение:
$P_{ном}=10^5$ (из справочника). По закону Менделеева-Клайперона:
$\{\table\PV={m_1}/{μ}·RT_1; \PV={m_2}/{μ}·RT_2;$ $⇒m_1-m_2={PVμ}/{R}({1}/{T_1}-{1}/{T_2})={10^5·60·0.029}/{8.31}({1}/{283}-{1}/{293})$.
$∆m=m_1-m_2=2.5кг$.
Задача 7
В баллоне, вместимость которого равна 25,6 л, находится 1,04 кг азота ($_{7}^{14}$N ) (двухатомный газ) при давлении 3,55 МПа. Определите температуру газа. Ответ округлите до десятых. Ответ выразите в (К).
Возьмите молярную массу азота $μ(N_2)=14·2·10^{-3}$кг/моль
Решение
Дано:
$V=25.6·10^{-3}м^3$
$m=1.04$кг
$μ(N_2)=28·10^{-3}$кг/моль
$p=3.55·10^6$Па
$R=8.31$Дж/моль·К
$T-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: $pV={m}/{μ}RT$(1), где $R$ - универсальная газовая постоянная. Из выражения (1) выразим $T$: $T={μpV}/{m·R}={28·10^{-3}·3.55·10^6·25.6·10^{-3}}/{1.04·8.31}=294.4K$.
Задача 8
Плоское зеркало движется со скоростью V = 1,5 см/с. С какой по модулю скоростью должен двигаться точечный источник света S, чтобы его отражение в плоском зеркале было неподвижным? Ответ выразите в (см/с).
Решение
Дано:
$υ=1.5м/с$
$U-?$
Решение:
Так как увеличивается расстояние от источника до зеркала "повторяется" внутри зеркала в изменении расстояния до изображения $U={1.5}*{2}={U}*{2}=3 м/с$.
Задача 9
Замкнутая электрическая цепь состоит их аккумулятора, внешней цепи сопротивлением R и амперметра. При сопротивлении R1 = 4,9 Ом амперметр показывает силу тока 2 А, а при сопротивлении R2 = 9,9 Ом — 1 А. Определите ЭДС аккумулятора. Ответ выразите в (В).
Решение
Дано:
$J_1=2A$
$J_2=1A$
$R_1=4.9$Ом
$R_2=9.9$Ом
$ε-?$
Решение:
Запишем закон Ома для полной цепи: $J_1={ε}/{R_1+r}$(1), $J_2={ε}/{R_2+r}$(2), где $ε$ - ЭДС аккумулятора, $r$ - внутреннее сопротивление аккумулятора. Из (1) и (2) имеем: $J_2R_2+J_2r=J_1R_1+J_1r$, откуда $r={J_2R_2-J_1R_1}/{(J_1-J_2)}={1·9.9-2·4.90}/{1}={0.1}/{1}=0.1$Ом. Тогда $ε=J_1R_1+J_1r=J_1(R_1+r)=2·(4.90+0.1)=10B$.
Задача 10
На сколько градусов Цельсия нагреется при штамповке кусок стали массой 1,5 кг от удара молота массой 400 кг, если скорость молота в момент удара равна 7 м/с? Считать, что на нагревание стали затрачивается 60% энергии молота. Ответ выразите в (◦С). (Удельная теплоёмкость стали $с=500$Дж/кг·°С)
Решение
Дано:
$m_1=1.5$кг
$m_2=400$кг
$υ=7м/с$
$Q=0.6E_к$
$с=500$Дж/кг·°С
$∆t-?$
Решение:
Кинетическая энергия молота в момент удара равна: $E_к={m_2υ^2}/{2}={400·49}/{2}=9800$Дж.(1)
Учитывая, что количество теплоты, полученное куском стали $Q$ равно: $Q=0.6E_к=cm_1∆t$(2), где $c$ - удельная теплоемкость стали. Тогда из (2) выразим $∆t$ и найдем его: $∆t={0.6E_к}/{cm_1}={0.6·9800}/{500·1.5}=7.84°С$
Задача 11
Автомобиль потребляет 10 л бензина на 100 км пути при скорости 108 км/ч. Определите КПД двигателя, если его мощность равна 50 кВт. Удельная теплота сгорания бензина 4,6 · 107 Дж/кг, плотность бензина ρ = 700 кг/м3.
Решение
Дано:
$V=10·10^{-3}м^3$
$ρ=700{кг}/{м^3}$
$q=4.6·10^7$Дж/кг
$S=10^5$м
$υ=108=30$м/с
$p=5·10^4Вт$
$η-?$
Решение:
КПД нагревателя определяется выражением: $η={A_{полез}}/{A_{затр}}·100%$(1), $A_{полез}=ρ·t$(2), где $t={S}/{υ}$(3) - время движения авто. $A_{затр}=Q=qm=q·ρ·V$(4), где $m=ρ·V$(5) - масса бензина. Подставим (2) и (4) с учетом (3) и (5) в (1) получим: $η={p·S}/{υ·q·ρ·V}·100%={5·10^4·10^5·100%}/{30·4.6·10^7·700·10^{-2}}={5·10^9·100%}/{9.66·10^9}=51.76%=51.8%$.
Задача 12
При помощи рассеивающей линзы получено уменьшенное 3 раза изображение предмета. На каком расстоянии от линзы расположено изображение, если фокусное расстояние линзы равно 60 см? Ответ в см.
Решение
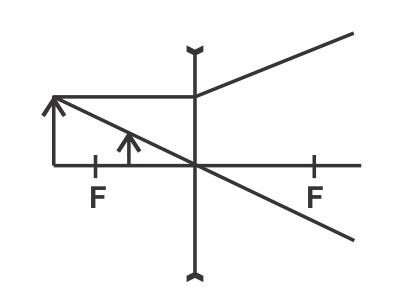
Пусть $a$ - расстояние от источника до линзы, $в$ - расстояние от изображения до линзы, $Г$ - линейное увеличение линзы, $Г={в}/{а}$
Формула тонкой линзы ${1}/{a}+{1}/{в}={1}/{F}$(так как линза рассеивающая, то $F=-60$см)
Решая, находим $в={aF}/{a-F}$
Подставим в $Г={F}/{a-F}$
По условию $|Г|={1}/{3}; {|F|}/{a+|F|}={1}/{3}⇒a=2|F|=120см⇒в={120·60}/{120+60}см=40(см)$
Задача 13
Вертикальное изображение свечи на экране, полученное с помощью выпуклой линзы оптической силой 2 дптр, оказалось в 1,5 раза больше её действительных размеров. На каком расстоянии от линзы была поставлена свеча? Ответ выразите в м и округлите до сотых.
Решение
Линейное увеличение линзы $Г=f/d=1.5$ (1), где $d$ - расстояние от источника до линзы, $f$ - расстояние от линзы до изображения.
$a$ и $f$ связаны друг с другом формулой тонкой линзы:${1}/{F}={1}/{d}+{1}/{f}⇒f={dF}/{d-F}$ (2).
Оптическая сила определяет фокусное расстояние: $D={1}/{F}⇒F={1}/{D}=0.5$м
Подставим (2) в (1):$Г={F}/{a-F}={3}/{2}⇒{{1}/{2}}/{a-{1}/{2}}={3}/{2}⇒a={5}/{6}≈0.83 м$
Задача 14
Тепловая машина работает при температуре нагревателя 577$°$С и температуре холодильника 237$°$С. Каков максимально возможный её КПД? Ответ в %.
Решение
Максимальное КПД будет у цикла Карно $T_x=(237+273)K=510K, T_н=(577+273)K=850K$
$η=1-{T_x}/{T_н}$
$η=1-{510}/{850}=1-0.6=0.4=40%$
Задача 15
Два проводника с сопротивлениями R1 = 5 Ом и R2 = 10 Ом соединены последовательно. Какова мощность тока в проводнике с сопротивлением R1, если мощность, выделяемая током на сопротивлении R2, равна 4 Вт? Ответ в Вт.
Решение
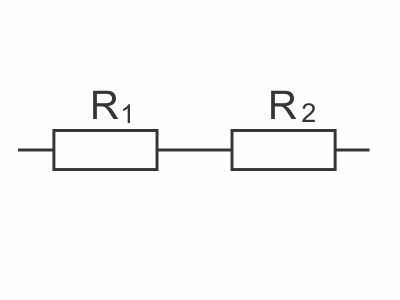
Резисторы соединены последовательно, следовательно, токи в них одинаковые.
$P=I^2R$
$\{\table\ P_1=I^2_1R_1; \ P_2=I^2_2R_2;$ $⇒{P_1}/{P_2}={R_1}/{R_2}⇒P_1=P_2{R_1}/{R_2}=2$Вт.
Задача 16
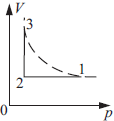
Два моля идеального одноатомного газа сначала охладили, а затем нагрели до первоначальной температуры 400 К, увеличив объём газа в три раза. Какое количество теплоты отдал газ на участке 1 – 2? Ответ в Дж (округлите до целых).
Решение
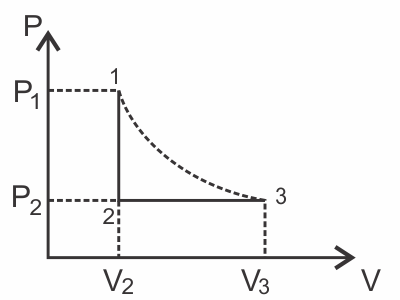
Нарисуем процесс в $PV$ координатах $V_3=3V_2; T_1=T_3=400K; υ=2$моль
Участок 12 - изохорное охлаждение, следовательно, работа на этом участке не совершается $A_{12}=0, Q_{12}=∆U_{12}$(I начало термодинамики)
$∆U_{12}={3}/{2}υR(T_2-T_1)$
Для поиска $T_2$ напишем уравнение Клайперона для участка 2-3: ${P_2V_2}/{T_2}={P_3V_3}/{T_3}; P_2=P_3$
Откуда $T_2={T_3}/{3}$
$Q_{12}=∆U_{12}={3}/{2}υR(T_2-T_1)={3}/{2}υR({T_1}/{3}-T_1)=-υRT_1=-6648$Дж
т. е. газ отдал ${6648}$Дж
Задача 17
В сосуд налили $2$ л воды при температуре $25°$C и поставили на огонь. Найдите, через сколько минут вода в сосуде закипит, если мощность горелки $7$ кВт. Теплоёмкостью сосуда пренебречь, считать, что вся выделяемая теплота идёт на нагревание воды.
Ответ напишите в следующих единицах измерения: «мин»
Решение
2 л воды имеют массу 2 кг. Для нагревания до кипения (100 С), то есть на $ΔT=75$ С требуется количество теплоты $Q=mcΔT$
Мощность горелки $N={Q}/{t}$, t - время
$t={mcΔT}/{N}={2*4200*75}/{7000}=90$ с = 1,5 мин
Задача 18
Через идеальный амперметр, включённый в цепь, как показано на рисунке, течёт ток $2$ А. Определите напряжение на сопротивлении $R_1$.
Решение
Дано:
$R_1=1$ Ом; $R_2=2$ Ом; $R_3=2$ Ом; $R_4=1$ Ом;
$I_2=2$ А;
Решение:
По закону Ома для участка цепи, напряжение на резисторе $R_1$: $U_1=I_1R_1$ (1)
Сила тока, протекающего через сопротивление $R_1$: $I_1=I_2+I_4$ (2)
$I_4$ - сила тока, протекающего через сопротивление $R_4$.
По закону Ома для участка цепи: $I_4={U_4}/{R_4}$ (3).
Напряжение на резисторе 4: $U_4=U_2+U_3$ (4),
т.к. $R_4$ соединён параллельно с последовательными сопротивлениями $R_2$ и $R_3$. (Напряжения на амперметре нет, так как он идеальный и его сопротивление равно нулю)
Через последовательно соединённые резисторы 2 и 3 протекает ток одинаковой силы, равный $I_2$, поэтому с учётом закона Ома для участка цепи уравнение (4) примет вид: $U_4=I_2(R_2+R_3)=2А(2+2) Ом=8 В$
Значит согласно (2) $I_1=2А+8А=10А$, тогда из (1) следует, что $U_1=10А*1Ом=10В$
Если получить конечную формулу без промежуточных вычислений:
$U_1=(I_2+I_4)R_1=(I_2+{U_4}/{R_4})R_1=(I_2+{I_2(R_2+R_3)}/{R_4})R_1$
Задача 19
В двух теплоизолированных баллонах объёмами $3$ л и $5$ л, соединённых трубкой с краном, находится гелий. В первом баллоне его температура равна $27°$С, а во втором баллоне — $127°$С. Давление газа в обоих баллонах одинаково. Какая температура установится в баллонах, если открыть кран?
Решение
| Дано | Анализ | Решение |
| $V_1=3л·10^{-3}м^3$ $V_2=5·10^{-3}м^3$ $T_1=300K$ $T_2=400K$ $P_1=P_2$ $T_3-?$ | $1)\{\table\PV_1=υ_1RT_1; \PV_2=υ_2RT_2;$$⇒$$\table\υ_1={PV_1}/{RT_1}; \υ_2={PV_2}/{RT_2};$ $P(V_1+V_2)=(υ_1+υ_2)RT_3$ $P(V_1+V_2)=({PV_1}/{RT_1}+{PV_2}/{RT_2})RT_3$ | $T_3={8·10^{-3}}/{{3·10^{-3}}/{300}+{5·10^{-3}}/{400}}$ $T_3=356K$ |
Задача 20
Найдите давление идеального газа, плотность которого равна $1,\!5$ кг/м$^3$, а средняя квадратичная скорость молекул $200$ м/с.
Ответ напишите в следующих единицах измерения: «кПа»
Решение
Дано: $ρ=1,5$ кг/м$^3$; $v=200$ м/с.
Решение:
$p=1/3nm_0v^2$
$n=N/V$,$N$ - число частиц, $V$ - объём;
$m_0=M/N$, $M$- масса газа
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

