Задание 2. Динамика, законы Ньютона. ЕГЭ 2026 по физике

За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 74.1%
Ответом к заданию 2 по физике может быть целое число или конечная десятичная дробь.

Алгоритм решения задания 2:

  1. Определи, какие силы действуют на тело или систему тел в описываемой ситуации.
  2. Установи, рассматривается ли равновесие тела или его движение под действием сил.
  3. Соотнеси ситуацию с формулировками законов Ньютона или правилом сложения сил.
  4. Выдели физические величины, характеризующие силы и движение тела.
  5. Примени соответствующий закон Ньютона или правило сложения сил для описания процесса.
  6. Проверь, что полученный результат согласуется с физическим смыслом сил и их взаимодействия.

Задачи для практики

Задача 1

На тело массой $m=2$ кг действуют две силы. Найти модуль ускорения тела, если одна клетка на рисунке соответсвует $1Н$. Ответ дать в $м/c^2$

Решение

Найдём результирующую силу, действующую на тело, с помощью теоремы Пифагора: $$F_{рез}^{2}=F_{1}^{2}+F_{2}^{2}=3^{2}+4^{2}=5^{2}$$ Тогда $F_{рез}= 5 {Н}$
Из второго закона Ньютона: $$a={F_{рез}}/{m}=5/2=2,5 {кг}$$

Ответ: 2.5
Показать решение
Бесплатный интенсив

Задача 2

К бруску массой 1 кг прикладывают силу 6 Н под углом 60° к горизонту. С какой силой брусок действует на поверхность? Ответ запишите в Н, округлив до десятых

Решение

Запишем 2 закон Ньютона.

$mg↖{-}+N↖{-}+F↖{-}=ma↖{-}$

Сила, c которой брусок действует на поверхность, называется вес. Согласно 3 закону Ньютона, вес бруска по модулю равен силе реакции опоры N: $P=N$

Проекция 2 закона Ньютона на вертикальную ось, направленную вверх: $-mg+N+Fsinα=0$, тогда $N+=mg-Fsinα$

$P=N=mg-Fsinα=1кг·10м/{c^2}-6·{√3}/2=4,8 H$

Ответ: 4.8
Показать решение
Бесплатный интенсив

Задача 3

Брусок массой 2 кг покоится на столе. Коэффициент трения между столом и брусок равен 0.1 . Какую силу надо приложить к бруску, чтоб сдвинуть его с места?

Решение

Сила, которая потребуется равна силе трения F = μmg = 0.1*2*10 = 2 Н.

Ответ: 2
Показать решение
Бесплатный интенсив

Задача 4

На рисунке показана зависимость проекции ускорения тела на ось х в зависимости от проекции суммы приложенных к телу сил. Найдите массу тела в (г).

Решение

По второму закону Ньютона: $$F_{x}=ma_{x}$$ Выберем любую точку и посчитаем для неё. Например при значении силы 3 Н, ускорение равно 4 ${м}/{{с}^{2}}$

Тогда получаем: $$m={F_{x}}/{a_{x}}=3/4=0,75 {кг}= 750 {г}$$

Ответ: 750
Показать решение
Бесплатный интенсив

Задача 5

На рисунке представлены графики зависимости модуля силы упругости, возникающей при растяжении пружин 1 и 2, от значения её деформации.

Каким будет удлинение второй пружины, если к ней подвесить тело массой 300 г. Ответ в (см)?

Решение

F=mg=3Н. Эта сила, которая будет действовать на 2 пружинку. Ищем по графику это удлинение - оно равно 50 см

Ответ: 50
Показать решение
Бесплатный интенсив

Задача 6

На рисунке представлен график зависимости модуля силы упругости, возникающей при растяжении пружины, от значения её деформации.

Чему равна жесткость 1 ой пружины? Ответ выразите в (H/м).

Решение

F=kx , от куда k = F/x - а это тангенс угла наклона, не забываем сантиметры перевести в метры. 5/0,1= 50 Н/м

Ответ: 50
Показать решение
Бесплатный интенсив

Задача 7

На брусок со стороны пола действует сила трения 2 Н. Чему равна сила трения, действующая на пол со стороны бруска?

Решение

По 3 Закону Ньютона эти силы будут раны

Ответ: 2
Показать решение
Бесплатный интенсив

Задача 8

Растяжение пружины, на которой висит грузик равна 1 см. Чему станет равно растяжение пружины, если дополнительно повесить еще один грузик, масса которого в 3 раза больше. Ответ выразите в см.

Решение

В начале kx1=mg , после kx2=(m+3m)g. То есть растяжение увеличится в 4 раза

Ответ: 4
Показать решение
Бесплатный интенсив

Задача 9

Первая космическая скорость на некоторой планете равна 5 км/с. Чему равна вторая космическая скорость на этой планете? Ответ выразите в км/с, округлив до целых

Решение

Первая космическая скорость $v_1=√{{GM}/{R}}$
Вторая космическая скорость $v_2=√{{2GM}/{R}}$
$v_2=√2*v_1=5*1.4=7$ км/с

Ответ: 7
Показать решение
Бесплатный интенсив

Задача 10

Ящик массой $1.5$ кг стоит на гладком льду. Его начинают толкать с постоянной горизотальной силой $9Н$. Через какое время ящик передвинут на $75$ метров? Отвпт приведите в (с)

Решение

F = ma, значит $a = {F}/{m}$ = 6 (м/с)

$ S=V_ot+ {at^2}/{2} $, т.к. $V_o = 0$, то$ t= √{{2S}/a}$ = 5 с.

Ответ: 5
Показать решение
Бесплатный интенсив

Задача 11

На брусок слева и справа действуют 2 пружины. При чем он в таком положении находится в покое. Первая пружина растянута на 1 см, вторая на 2 см. Жесткость 1 пружины равна 100 Н/м. Чему равна жесткость второй пружины?

Решение

Если брусок находится в покое, значит сила упругости слева равна силе упругости справа. То есть k1x1 = k2x2. 0.01*100=0.02*k2.

Ответ: 50
Показать решение
Бесплатный интенсив

Задача 12

По гладкой поверхности движется брусок массой 1кг с ускорением 2 м/c. Движется он за счет того, что его тянут с помощью динамометра. При чем растяжение пружины составляет 1 см. Чему равна жесткость пружины? Ответ представить в (Н/м)

Решение

По второму закону Ньютона для груза, записанному в проекции на горизонтальную ось, сонаправленную с ускорением: $F_упр = ma$ (Сила тяжести и сила реакции опоры отсутствуют в уравнении, так как они вертикальные). Сила упругости задаёт ускорение бруску. По определению модуль силы упругости $F_упр = k|x|$
Тогда получим^ $k|x| = ma$, следовательно $k={ma}/{|x|}={ 1кг*2м / c^2}/{0.01м}=200$ Н/м.

Ответ: 200
Показать решение
Бесплатный интенсив

Задача 13

Прямоугольный брусок движется вдоль стола. На него действует сила трения F. Во сколько раз изменится сила трения, если перевернули брусок и его площадь основания увеличилась в 2 раза?

Решение

Сила трения определяется коэффициентом трения и силой реакции опоры. Тогда соответственно ничего не изменится.

Ответ: 1
Показать решение
Бесплатный интенсив

Задача 14

На горизонтальной поверхности лежит металлический брусок массой 4 кг. Для того чтобы сдвинуть этот брусок с места, к нему нужно приложить горизонтально направленную силу 20 Н. Затем на эту же поверхность кладут пластиковый брусок массой 1 кг. Коэффициент трения для пластика o данную поверхность в 5 раз меньше, чем для металла. Какую горизонтально направленную силу нужно приложить к пластиковому бруску для того, чтобы сдвинуть его с места? Ответ выразить в (H).

Решение

Дано:

$m_1=4$кг

$F_1=20$Н

$m_2=1$кг

${M_1}/{M_2}=5$

$F_2-?$

Решение:

По третьему закону Ньютона составим 2 уравнения для металлического (1) и пластикового (2) бруска.

$\{\table\F_{тр}^1=F_1; \F_{тр}^2=F_2;$ $⇒$ $\table\M_1·m_1g=F_1; \M_2·m_2·g=F_2;$ ${M_1m_1}/{M_2m_2}={F_1}/{F_2}$

$F_2={F_1·M_2·m_2}/{M_1·m_1}={20·1}/{5·4}=1H$

Ответ: 1
Показать решение
Бесплатный интенсив

Задача 15

Справедлив ли (да, нет) закон всемирного тяготения $F = G{m_1·m_2}/{R^2}$ для расчёта силы гравитационного притяжения между следующими двумя телами? Ответ запишите словом.

Решение

Нет, закон всемирного тяготения для расчета сил гравитационного притяжения несправедлив, т.к. он справедлив для мат. точек и шаров однородных.

Ответ: нет
Показать решение
Бесплатный интенсив

Задача 16

Два искусственных спутника Земли массами 200 кг и 400 кг обращаются по круговым орбитам одинакового радиуса. Чему равно отношение скоростей этих спутников v2/v1?

Решение

Дано:

$m_1=200$кг

$m_2=400$кг

$R_1=R_2; M-$масса Земли

${υ_2}/{υ_1}-?$

Решение:

При вращении любого тела по окружности вокруг Земли центробежная сила уравновешивается гравитационным полем Земли:${υ^2}/{R}m=G{m·M}/{R^2}⇒{υ^2}/{R}=G{M}/{R^2}⇒υ=√{G{M}/{R}}$. Заметим, что скорость не зависит от массы тела, а зависит только от радиуса. Следовательно, скорости одинаковы.

Ответ: 1
Показать решение
Бесплатный интенсив

Задача 17

К ящику массой 10 кг, стоящему на горизонтальной шероховатой поверхности, приложили горизонтальную силу 30 Н, под действием которой он начал двигался вдоль этой поверхности равномерно и прямолинейно. Определите коэффициент трения между ящиком и поверхностью.

Решение

Дано:

$m=10$кг

$F=30H$

$υ=const$

$μ-?$

Решение:

По третьему закону Ньютона: $F=F_{тр}=μmg⇒μ={F}/{mg}$

$μ={30}/{10·10}=0.3$.

Ответ: 0.3
Показать решение
Бесплатный интенсив

Задача 18

Найдите, чему равно ускорение свободного падения на некоторой планете, если период колебаний секундного земного математического маятника на ней оказался равным 1,41 с. Ответ выразите в (м/с2).

Решение

Дано:

$g_n-?$

$T_n=1.41$с

$T_3=1c$

Решение:

$\{\table\T_n=2π√{{l}/{g_n}}; \T_3=2π√{{l}/{g_3}};$ ${T_n}/{T_3}=√{{g_3}/{g_n}}; {1.41^2}/{1}={10}/{g_n}$

$g_n=5м/с^2$

Ответ: 5
Показать решение
Бесплатный интенсив

Задача 19

К лежащему на горизонтальном столе телу массой 2 кг приложили горизонтальную силу, равную 5 Н. Коэффициент трения тела о поверхность стола 0,4. Чему равна сила трения, действующая на тело? Ответ выразите в (H).

Решение

Дано:

$m=2$кг

$F=5H$

$μ=0.4$

$F_{тр}-?$

Решение:

1) По третьему закону Ньютона $F_1=-F_2$ сила действия равна силе противодействие.

Ответ: 5
Показать решение
Бесплатный интенсив

Задача 20

Результаты эксперимента по определению зависимости длины резинового жгута от модуля приложенной к нему растягивающей силы представлены в таблице. Какова жёсткость жгута на линейном участке по результатам эксперимента?

l, м 0,8 0,9 1,0 1,1 1,15
F, H 0 1 2 3 4

Ответ выразите в (Н/м).

Решение

Дано:

$l_0=0.8$м

$l=0.9$м

$F=1H$

$k-?$

Решение:

Начальная длина жгута $l_0=0.8$м, т.к. при силе $F=0H$ длина жгута равна $0.8$м. По закону Гука имеем: $F=k·(l-l_0)$(1)

При длине жгута $l=0.9$м сила $F=1H$, тогда из (1) имеем: $k={F}/{l-l_0}$(2). Подставим числа: $k={1}/{(0.9-0.8)}={1}/{0.1}=10$Н/м.

Ответ: 10
Показать решение
Бесплатный интенсив
Показать еще

Рекомендуемые курсы подготовки

егэ по физике физика 11 класс физика 11 класс физика акции физика с нуля

О чем задание?

Второе задание ЕГЭ относится к блоку “Механика”, теме “Динамика” и за него можно получить 1 балл. Следует решить задачу и получить численный ответ. Для решения этой задачи необходимо знать законы Ньютона, закон всемирного тяготения, закон Гука, силу трения формулы по этим подразделам.

Алгоритм решения:

Первым делом определите, какие силы действуют на тело (тела). Если речь идет ни об одной силе, а о нескольких, то необходимо нарисовать тело и расставить силы с учетом направления. Далее следует выбрать 2 оси и сделать проекцию действующих сил на OX и OY.

Если речь идет про одну силу, то очень часто встречается задание, где необходимо определить, во сколько изменится та или иная величина. Для этого надо расписать “до” и “после” и поделить одно на второе.

Если речь идет про определенную силу и необходимо что-то рассчитать, воспользуйтесь формулой. Но не забывайте перевести в систему СИ, а также учтите важные особенности (например, существует сила трения и сила скольжения, и необходимо помнить, при каких условиях по какой формуле эту силу трения считать).

Примеры решения задач

Пример 1.

Каково ускорение свободного падения на высоте равной четверти Земного радиуса? Ответ в м/с2

Решение

Пример 2.

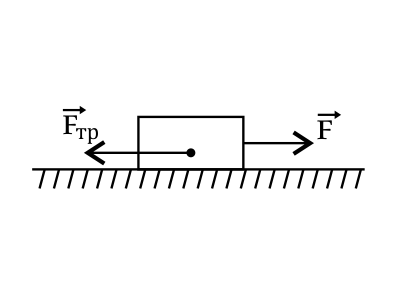
К лежащему на горизонтальном столе телу массой 2 кг приложили горизонтальную силу, равную 2 Н. Коэффициент трения тела о поверхность стола 0,4. Чему равна сила трения, действующая на тело? Ответ выразите в (H).

Решение

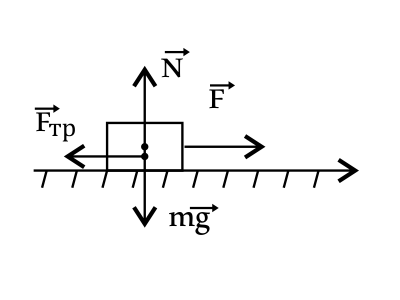
1) Смотрим на выполнение условий проверки.

2) По оси OY действует 2 только силы N и mg и они противоположно направлены. Следовательно N = mg = 2*10 = 20 Н

3) Проверяем по условию μN = 8 Н, что меньше cилы F = 2Н (приложенная сила). Тогда применяем первую формулу для силы трения покоя. |Fтр| = |F| = 2Н

Пример 3.

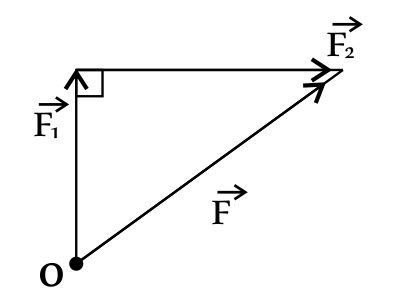
Равнодействующая двух взаимно перпендикулярных сил, одна из которых составляет 3 Н, равна 5 Н. Каков модуль второй силы? Ответ выразите в (H).

Решение

Популярные материалы
  • Без воды
  • Ламповая атмосфера
  • Крутые преподаватели

ЕГЭ 2027: бесплатный курс
по физике

На бесплатном демо-курсе ты:
  • 🔥 Получишь мощный старт для дальнейшей подготовки.
  • 🔥 Прокачаешь свою Кинематику.
  • 🔥 Узнаешь все о Линзах в ЕГЭ.
  • 🔥 Будешь решать задачи с дифракционной решеткой на ИЗИ.
  • 🔥 Улучшишь свои резы на 20 вторичных баллов ЕГЭ.

Что тебя ждет?

  • 👉 7 вебинаров (по 1 вебчику в неделю: согласись, не напряжно, да?).
  • 👉 Домашка после каждого веба (без дедлайна, лето все-таки, делай, когда удобно).
  • 👉 Скрипты и конспекты, полезные материалы к каждому занятию.
  • 👉 Личный кабинет Турбо (это супер-мега удобная площадка 🔥).
  • 👉 Тренажёр для отработки заданий (все в том же личном кабинете).
  • 👉 Отдельная беседа с преподавателями и однокурсниками.
  • 👉 Комфортная атмосфера, эффективная подготовка + чувство, что лето проводишь не зря 🔥.
Получи бесплатный демо-доступ
Оставь заявку и займи место
на бесплатном курсе Турбо ЕГЭ
Нажимая на кнопку «Отправить», вы принимаете положение об обработке персональных данных.
Бесплатная летняя школа
Проведи это лето
С пользой
Проведи это лето с пользой
Подробнее