Задание 3. Законы сохранения в механике . ЕГЭ 2026 по физике
Средний процент выполнения: 82.2%
Ответом к заданию 3 по физике может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 3:
- Определи, какой физический процесс рассматривается: изменение импульса, совершение работы или изменение механической энергии.
- Выдели физические величины, относящиеся к импульсу, работе или энергии, и установи, какие из них заданы в условии.
- Соотнеси описанный процесс с соответствующим законом или теоремой: законом сохранения импульса, теоремой об изменении кинетической энергии или законом сохранения механической энергии.
- Запиши применимый закон или формулу в общем виде с использованием физических величин.
- Подставь значения величин из условия задания или выполни логический вывод на основе записанного закона.
- Проверь, что полученный результат согласуется с физическим смыслом импульса, работы и энергии.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
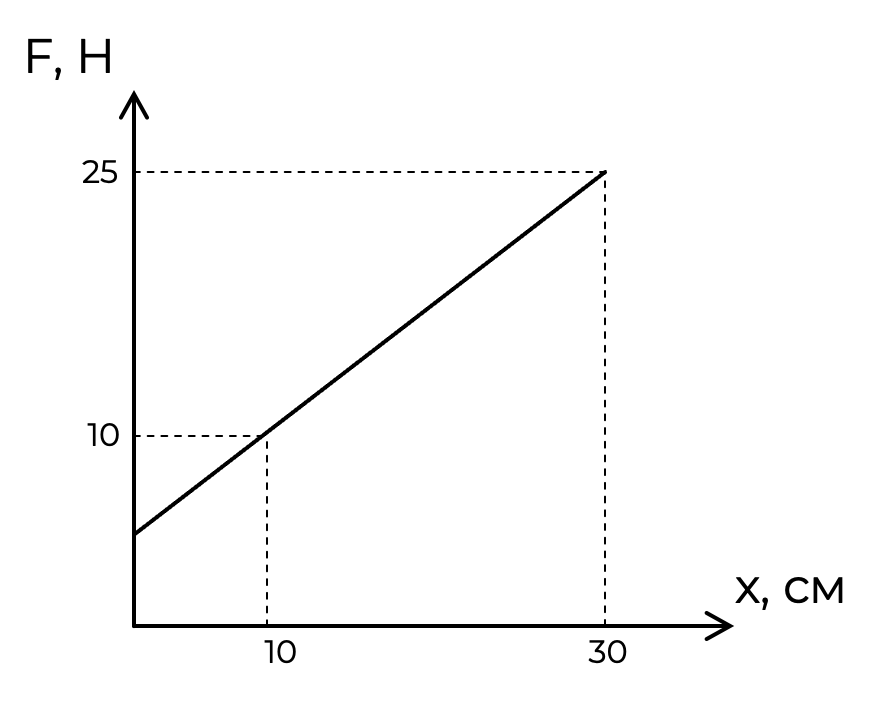
На графике представлена зависимость силы упругости от координата груза, прикреплённого к пружине. Какую работу совершила сила упругости при перемещении груза от координаты х = 10 см до 30 см?
Решение
Сила упругости - потенциальная сила, поэтому её работу можно найти как площадь под графиком F(s). Найдём площадь трапеции как полусумму оснований на высоту.
$$A_{упр}={10 {Н} + 25 {Н}}/{2} (30 {см} - 10 {см})={10 {Н} + 25 {Н}}/{2} (0,3 {м} - 0,1 {м})=3,5 {Дж}$$
Задача 2
Координата тела массой 2 кг, движущегося вдоль оси х под действием горизонтальной силы F, изменяется по закону: $x(t)=7+10t-5t^2$ Определите кинетическую энергию тела в момент времени $t=3$ c.
Решение
Дано:
$m=2$кг
$x(t)=7+10t-5t^2$
$t=3c$
$E_{кин}$ = ?
Решение:
$E_{кин}={mv^2}/2$, где $v$ - скорость тела. Найдём скорость тела в момент времени $t=3c$
В общем виде $$x(t)=x_{0}+v_{0}t+ {at^2}/{2}$$, где $x_{0}$ - начальная координата тела, $v_{0x}$ - проекция начальной скорости тела на ось х, $a_{x}$ - проекция ускорения тела на ось х. В нашем случае зависимости координаты тела от времени: $$𝑥(𝑡)=7+10𝑡-5𝑡^2$$ Тогда $x_{0}=7$ м, $v_{0}=10$ м/с, $a_{x}=-10 {м}/{{с}^2}$
Зависимость скорости тела от времени $$v(t)=v_{0}+at=10-10t$$
Тогда: $$v(t=3)=10-10*3=10-30=-20 {м}/{c}$$
Найдём кинетическую энергию тела: $E_{кин}={mv^2}/2={2*{(-20)}^{2}}/{2}=400$ Дж
Ответ: 400 Дж
Задача 3
Координата тела массой 2 кг, движущегося вдоль оси х под действием горизонтальной силы F, изменяется по закону: $x(t)=7+10t-5t^2$ Какую работу совершила сила F за 3 с? .
Решение
Дано:
$m=2$кг
$x(t)=7+10t-5t^2$
$t=3c$
$A_{F}$ = ?
Решение:
по теореме о кинетической энергии: $A_{F}=E_{кин2} - E_{кин1}$, где $E_{кин2}$ и $E_{кин1}$ - кинетическая энергия тела в конце движения и в начале движения соответственно
$E_{кин}={mv^2}/2$, где $v$ - скорость тела. Найдём скорость тела в момент времени $t=3c$
В общем виде $$x(t)=x_{0}+v_{0}t+ {at^2}/{2}$$, где $x_{0}$ - начальная координата тела, $v_{0x}$ - проекция начальной скорости тела на ось х, $a_{x}$ - проекция ускорения тела на ось х. В нашем случае зависимости координаты тела от времени: $$𝑥(𝑡)=7+10𝑡-5𝑡^2$$ Тогда $x_{0}=7$ м, $v_{0}=10$ м/с, $a_{x}=-10 {м}/{{с}^2}$
Зависимость скорости тела от времени $$v(t)=v_{0}+at=10-10t$$
Тогда: $$v(t=3)=10-10*3=10-30=-20 {м}/{c}$$
Найдём кинетическую энергию тела через 3 с: $E_{кин2}={mv^2}/2={2*{(-20)}^{2}}/{2}=400$ Дж
Кинетическая энергия в начальный момент времени $E_{кин1}={m{v_{0}}^2}/{2}={2*{10}^{2}}/{2}=100$ Дж
Тогда: $A_{F}=E_{кин2} - E_{кин1} = 400 - 100 = 300$ Дж
Ответ: 300 Дж
Задача 4
Яблоко, массой 200 г, падало Ньютону на голову с дерева высотой 5 м. Найдите, какую работу при этом совершила сила тяжести, если Ньютон был ростом 1,8 м.
Решение
Дано:
$H= 5{м}$
$m= 200{г}=0,2 {кг}$
$h = 1,8 {м}$
$A_{тяж}= ?$
Сила тяжести - потенциальная сила. Поэтому её работу можем найти как изменение потенциальной энергии тела со знаком минус: $$A_{тяж}= -Δ E_{пот}= E_{пот1} - E_{пот2} = mgH-mgh=mg(H-h)= 0,2 * 10* (5-1,8) =6,4 {Дж}$$
Ответ: 6,4 Дж
Задача 5
Найдите работу силы тяжести, под действием которой тело массой 15 кг перемещается вертикально вверх на 50 см.
Решение
Дано:
m = 15 {кг}
Δ h = 50 {см} = 0,5 {м}
$A_{тяж}= ?$
Сила тяжести - потенциальная сила. Поэтому её работу можем найти как изменение потенциальной энергии тела со знаком минус: $$A_{тяж}= -Δ E_{пот}= E_{пот1} - E_{пот2} = mgh_{1}-mgh_{2}=mg(h_{1}-h_{2})=mg - Δ h=-15*10*0,5=-75 {Дж}$$
Ответ: -75 Дж
Задача 6
Найдите работу силы, равной 10 Н, если под действием этой силы тело, движущееся прямолинейно равномерно по горизонтальной поверхности, проходит расстояние 50 см. Угол между направлением силы и направлением движения - 45 ̊ . Ответ округлите до десятых
Решение
Дано:
$F=10$ Н
$S = 50 {см} = 0,5 {м} $
$Α = 45^{o}$
$A_{F}$ = ?
Решение:
Работу силы F можно найти по формуле $$A_{F}=FS*cos{Α}$$
Тогда: $$A_{F} = 10 * 0,5 * {√ 2}/{2} = 3,5{Дж}$$
Ответ: 3,5 Дж
Задача 7
Какую работу совершают силы сопротивления при остановке самолёта массой 30 т, движущегося по посадочной полосе со скоростью 360 км/ч? Ответ выразите в МДж
Решение
Дано:
$m=30 {т}= 30 * {10}^{3} {кг}$
$v_{1}=360 {км}/{ч}= 100 {м}/{с} $
$A_{сопр}$ = ?
Решение:
по теореме о кинетической энергии: $A_{сопр}=E_{кин2} - E_{кин1}$, где $E_{кин2}$ и $E_{кин1}$ - кинетическая энергия тела в конце движения и в начале движения соответственно
$E_{кин}={mv^2}/2$, где $v$ - скорость тела. В начале движения скорость тела была равна $v_{1}=100 {м}/{с} $, В конце движения самолёт остановился, поэтому скорость тела $v_{2}=0 {м}/{с}$
Тогда $$E_{кин1}={m{v_{1}}^2}/2={30 * {10}^{3} * {100}^{2} }/{2}=1,5 * {10}^{8} {Дж} = 150 {МДж}$$
$$E_{кин2}={m{v_{2}}^2}/2={30 * {10}^{3} * {0}^{2} }/{2}=0 {Дж} $$
Итого: $$A_{сопр}=E_{кин2} - E_{кин1}=0-150=-150 {МДж}$$
Ответ: -150 МДж
Задача 8
Тело массой 200 г, двигаясь равномерно, обладает импульсом 4 кг·м/с. Какова его кинетическая энергия? Ответ выразите в (Дж).
Решение
Дано:
$m=200г=0.2кг$
$p=4{кг·м}/{с}$
$Е_к-?$
Решение:
Импульс по определению равен: $p=mυ$(1), а кинетическая энергия определяется выражением:$Е_к={mυ^2}/{2}$(2).
Учитывая, что $mυ^2={m^2υ^2}/{m}={(mυ)^2}/{m}={p^2}/{m}$(3), подставим (3) в (2): $Е_к={p^2}/{2m}$(4).
Подставим числовые значения в (4): $Е_к={4^2}/{2·0.2}={16}/{0.4}=40$Дж
Задача 9
Тела 1 и 2 взаимодействуют только друг с другом. Изменение кинетической энергии тела 1 за некоторый промежуток времени равно 15 Дж. Работа, которую совершили за этот же промежуток времени силы взаимодействия тел 1 и 2, равна 45 Дж. Чему равно изменение кинетической энергии тела 2 за это время? Ответ выразить в (Дж).
Решение
Дано:
$∆E_1=15$Дж
$∆E_в=45$Дж
$∆E_2-?$
Решение:
По закону сохранения энергии запишем уравнение взаимодействия: $∆E_1+∆E_2=∆E_в⇒∆E_2=∆E_в-∆E_1$
$∆E_2=45-15=30$Дж
Задача 10
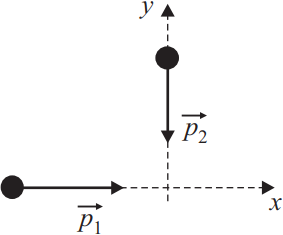
Два шарика движутся по гладкой горизонтальной плоскости вдоль осей Ox и Oy. Найдите модуль импульса второго шарика, если модуль импульса первого p1 = 1, 6 кг·м/с, а импульс системы этих шариков после их абсолютно неупругого удара 2 кг·м/с. Ответ выразить в (кг·м/с).
Решение
Дано:
${p_1}↖{→}=1.6$кгм/с
${p_{об}}↖{→}=2$кгм/с
${p_2}↖{→}-?$
Решение:
${p_{об}}↖{→}={p_1}↖{→}+{p_2}↖{→}$ - закон сохранения импульса для не упругого удара.
$2^2=1.6^2+p_2^2; {p_2}↖{→}=√{2^2-1.6^2}=1.2$кгм/с
Задача 11
Санки массой 50 кг из состояния покоя съезжают с гладкой наклонной плоскости высотой 5 м. После этого они продолжают двигаться по горизонтальной поверхности и спустя некоторое время останавливаются. Как при этом изменилась их механическая энергия? В ответе запишите: уменьшилась на _ (кДж).
Решение
Дано:
$m=50$кг
$h=5$м
$∆E_m-?$
$m_0=1·10^{-6}$кг
Решение:
По закону сохранения $∆E_m=∆E_h+∆E_к; ∆E_к=0$
$∆E_r=mgh=50·5·10=2.5$кДж. Тогда $∆E_{мех}=∆E_n=2.5$кДж.
Задача 12
Мальчик столкнул санки массой 2 кг с вершины горки. Сразу после толчка санки имели скорость 4 м/с, а у подножия горки она равнялась 8 м/с. Трение санок о снег пренебрежимо мало. Какова высота горки? Ответ выразите в (м).
Решение
Дано:
$υ_0=4$м/с
$υ_к=8$м/с
$F_{тр}=0$
$H-?$
Решение:
Запишем закон сохранения энергии для данного случая $E_{к_0}+E_п=E_к^к$. $E_{к_0}$ - кинетическая энергия в начальный момент; $E_п$ - потенциальная энергия в начальный момент; $E_к^к$ - кинетическая энергия в конце пути.
$E_п=E_к^к-E_{к_0}$
$mgH={m·υ_к^2}/{2}-{m·υ_0^2}/{2}$
$2·10·H=64-16⇒H=2.4$м
Задача 13
Автомобиль массой 1 т двигался со скоростью 72 км/ч. Максимальное значение коэффициента трения шин о дорожное покрытие равно 0,7. Каков минимальный тормозной путь автомобиля? Ответ округлите до целых. Ответ выразите в (м).
Решение
Дано:
$m=1000$кг
$υ=72км/ч=20м/с$
$g≈10м/c^2$
$μ_{max}=0.7$
$S_{min}-?$
Решение:
Работа силы трения равна изменению кинетической энергии автомобиля: $A_{F_{тр}}=∆E_к$(1), где $A_{F_{тр}}=F_{тр}·S_{min}·cos180°$(2). $∆E_к=0-{mυ^2}/{2}=-{mυ^2}/{2}$(3), т.к. автомобиль останавливается; $cos180°=-1$
$F_{тр}=μ_{max}·N=μ_{max}·mg$(4).
Подствим (2), (3), (4) в выражение (1): $-μ_{max}·mg·S_{min}=-{mυ^2}/{2}⇒S_{min}={υ^2}/{2μ_{max}·g}$(5)
$S_{min}={400}/{2·0.7·10}=28.57м=29м$
Задача 14
Тело массой 2 кг начинает свободно падать с высоты 5 м. Чему равна кинетическая энергия тела на высоте 2 м от земли? Ответ выразите в (Дж).
Решение
Дано:
$m=2$кг
$g=10м/с^2$
$h_1=5$м
$h_2=2$м
$E_{к_2}-?$
Решение:
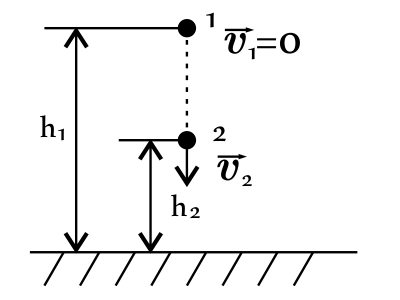
Полная механическая энергия тела в точке 1 равна полной механической энергии тела в точке 2: $E_1=E_2$(1), где $E_1=E_{п_1}+E_{к_1}=mgh_1+{mυ_1^2}/{2}=mgh_1$(2), $E_2=E_{п_2}+E_{к_2}=mgh_2+E_{к_2}$(3).
Подставим (2) и (3) в (1) и найдем $E_{к_2}:mgh_1=mgh_2+E_{к_2}$, откуда $E_{к_2}=mg(h_1-h_2)$(4).
Подставим числовые значения в (4), получим: $E_{к_2}=2·10·(5-2)=60$Дж.
Задача 15
Ученик исследовал зависимость силы упругости F пружины от её растяжения x и получил следующие результаты:
| F, H | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| x, см | 0 | 2 | 4 | 6 | 8 | 10 |
По данным опыта определите, какую работу нужно совершить, чтобы растянуть пружину от 4 см до 8 см. Ответ выразите в (Дж).
Решение
Дано:
$x_1=4см=4·10^{-2}м$
$x_2=8см=8·10^{-2}м$
$A-?$
Решение:
Работа силы упругости пружины равна убыли ее потенциальной энергии: $A={kx_1^2}/{2}-{kx_2^2}/{2}$(1), где $k$ - жесткость пружины.
Найдем жесткость пружины $k$. Для этого возьмем любые значения силы упругости пружины и растяжения, отличные от нуля, например, $F_{тр}=1H, x=0.04м$. Тогда, по закону Гука имеем: $F_{упр}=kx⇒k={F_{упр}}/{х}$(2). $k={1}/{0.04}=25Н/м$
Подставим числовые значения в (1) и найдем работу $A$: $A={25}/{2}((4·10^{-2})^2-(8·10^{-2})^2)=12.5·(16·10^{-4}-64·10^{-4})=-600·10^{-4}=-0.06$Дж.
Зная, что "минус" говорит о том, что при растяжении сила упругости направлена противоположно растяжению пружины.
Задача 16
Материальная точка равномерно движется по окружности со скоростью 2 м/с. Чему равна её масса, если изменение её импульса при повороте на 45◦ составило 9,2 · √2 кг·м/с? Ответ выразите в (кг).
Решение
Дано:
$υ=2$м/с
$α=45°$
$∆p↖{→}=9.2√2кгм/с$
$m-?$
Решение:
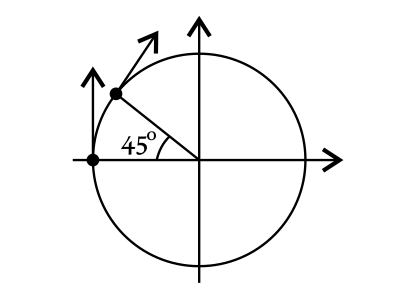
По определению: изменение импульса тела $∆p$ – это векторная разность между конечным $p_2$ и начальным $p_1$ импульсом тела. Тогда, применяя геометрические знания, по правилу вычитания векторов построим треугольник импульсов: начала векторов $p_1$ и $p_2$ совместим в одной точке, тогда получим третью сторону $∆p$ . Причем угол между сторонами, являющимися графическим изображением конечного и начального импульсов, будет заданный угол $α$.
Перейдем от векторов к скалярному выражению. По теореме косинусов имеем: ${∆p}^2={p_1}^2+{p_2}^2-2p_1p_2cosα$
По определению: импульс тела равен произведению массы тела на его скорость. Значит, по модулю векторы импульсов p1 и p2 равны между собой, так как движение равномерное: v=const, масса точки также не меняется. Имеем ${p_1}={p_2}=p=mv$. Тогда (1) примет вид:
${∆p}^2=2{p}^2-2p^2cosα$
${∆p}=√2{p}√{1-cosα}=√2{mv}√{1-cosα}$
Задача 17
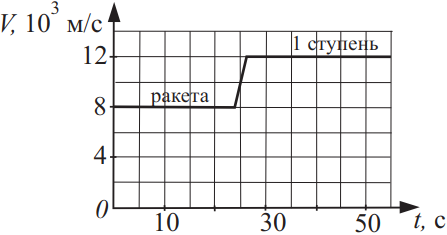
На экране монитора в Центре управления полётом отображены графики скоростей многоступенчатой ракеты массой 50 т и одной из ступеней массой 10 т. Чему равна скорость отделившейся второй ступени? Ответ выразите в (км/с).
Решение
Дано:
$m=50·10^3$кг
$υ=8·10^3$м/с
$m_1=10·10^3$кг
$υ_1=12·10^3$м/с
$υ_2-?$
Решение:
Запишем закон сохранения импульса: импульс ракеты равен сумме импульсов первой и второй ступеней: $mυ=m_1υ_1+m_2υ_2$(1), где $m_2=m-m_1$(2), $m, m_1, m_2$ - массы ракеты первой и второй ступеней; $υ, υ_1, υ_2$ - скорости ракеты первой и второй ступеней. Выразим из (1) скорость $υ_2$ с учетом (2): $υ_2={mυ-m_1υ_1}/{(m-m_1)}={50·10^3·8·10^3-10·10^3·12·10^3}/{40·10^3}={400·10^6-120·10^6}/{40·10^3}={280·10^6}/{40·10^3}=7·10^3=7км/с$
Задача 18
На покоящуюся тележку массой 0,2 т налетает тележка массой 0,3 т со скоростью 8 км/ч . Найдите скорость, с которой эти тележки начали двигаться совместно после удара. Ответ выразите в (км/ч).
Решение
Дано:
$m_1=200$кг
$m_2=300$кг
$υ_1=8{км}/ч$
$υ_2-?$
Решение:
По закону сохранения энергии $m_1·0+m_2·υ_1=(m_1+m_2)υ_2$ выразим: $υ_2={m_2·υ_1}/{m_1+m_2}={300·8}/{200+300}=4.8{км}/ч$
Задача 19
Легковой автомобиль и грузовик движутся со скоростями 108 км/ч и 72 км/ч соответственно. Масса грузовика 4500 кг. Какова масса легкового автомобиля, если импульс грузовика больше импульса легкового автомобиля в 2 раза? Ответ выразите в (кг).
Решение
Дано:
$υ_л=108$км/ч$=30м/с$
$υ_г=72$км/ч$=20м/с$
$m_г=4500кг$
$p_г=2p_л$
$m_л-?$
Решение:
По определению импульс тела равен: $p=mυ$(1), тогда $p_г=m_г·υ_г$(2) - импульс грузового автомобиля; $p_л=m_л·υ_л$(2) - импульс легкового автомобиля. По условию задачи: $p_г=2p_л$(4). Подставим (2) и (3) в (4): $m_г·υ_г=2m_лυ_л⇒m_л={m_г·υ_г}/{2υ_л}$(5). Подставим числовые значения в (5): $m_л={4500·20}/{30·2}=1500кг$.
Задача 20
В цистерне поливочной автомашины массой 4 т находится 5 м3 воды. Чему равен импульс машины, когда она движется со скоростью 18 км/ч? Ответ выразите в (кг·м/с).
Решение
Дано:
$m_1=4·10^3$кг
$ρ=1000{кг}/{м^3}$
$V=5м^3$
$υ=18 км/ч=5$м/с
$p-?$
Решение:
Импульс поливочной машины по определению равен: $p=mυ$(1), где $m=m_1+m_2$(2), где $m_2=ρ·V$(3) - масса воды в цистине, $m$ - масса автомашины с водой. Подставим (3) в (2), а затем в (1), учитывая, что $ρ$ - плотность воды: $p=mυ=(m_1+m_2)υ=(m_1+ρ·V)·υ=(4·10^3+10^3·5)·5=9000·5=45000{кг·м}/{с}$.
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

