Задание 1. . ЕГЭ 2022 по физике

Алгоритм решения задания 1:

1. Первым делом определите, на какой вид движения задача (равномерное, равноускоренное и т.д).
2. Далее посмотрите, что вам необходимо найти. Обратите внимания на ключевые слова: МОДУЛЬ, ПРОЕКЦИЯ, ПУТЬ, ПЕРЕМЩЕНИЕ. Так как именно на этих словах вас хотят подловить.
3. Выбирайте наиболее подходящую для решения формулу.

Примеры задач и краткая теория:

Задание 1

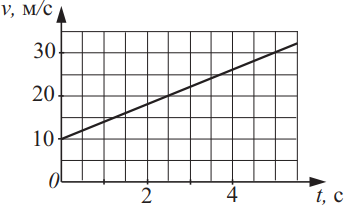
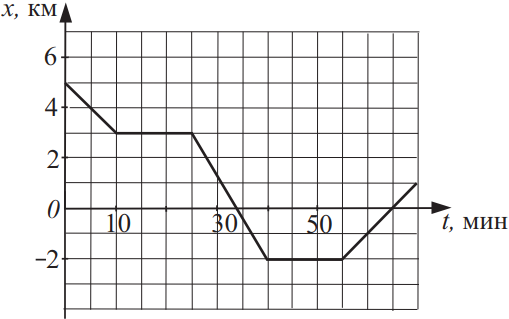
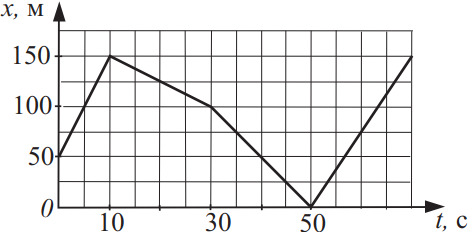
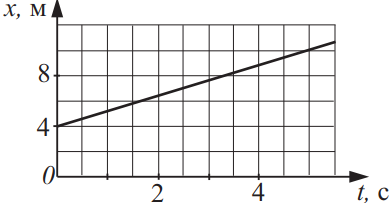
Чаще всего вам дан график зависимости либо координаты, либо скорости от времени, и необходимо найти: путь, перемещение, скорость, ускорение

Ниже дан скелет решения задач такого плана.

Задание 2

Автомобиль разгоняется на прямолинейном участке пути , и зависимость координаты x тела от времени t задаётся уравнением x = 3 − 5t + t2. Какова проекция скорости тела на ось Ox в момент времени 2 с? Ответ выразите в (м/c).

Ответ: -1 (м/c).