Задание 26. Механика (расчетная задача высокого уровня с обоснованием). ЕГЭ 2026 по физике
Средний процент выполнения: 12.4%
Ответом к заданию 26 по физике может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Алгоритм решения задания 26:
- Определи, какие разделы механики используются в задаче.
- Выбери физическую модель, описывающую систему тел и условия задачи.
- Обоснуй применимость выбранной модели к данной ситуации.
- Выдели физические величины и параметры, заданные в условии.
- Запиши законы и формулы, относящиеся к выбранным разделам механики.
- Составь расчётные соотношения на основе выбранных законов.
- Выполни вычисления в логически обоснованной последовательности.
- Проверь результат на соответствие физическому смыслу и условиям задачи.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Шар массой 1 кг кинули вертикально вниз с высоты 20 м с нулевой начальной скоростью на горизонтальную поверхность. После отскока шар имел кинетическую энергию 128 Дж. Определите время соударения шарика с землёй, если средняя сила удара равна 1000 Н. Действием силы тяжести при соударении можно пренебречь. Сопротивление воздуха пренебрежимо мало
Какие законы Вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Найдём скорость перед ударом о землю по ЗСЭ:
$mgh=mv_{1}^2/2$
откуда ясно, что $v_{1}=(2gh)^{1/2}=20 м/с $
Зная, что кинетическая энергия после удара 212 Дж, найдём скорость шара после удара $v_{2}=(2E/m)^{1/2}=16 м/с$
Введём вертикальную ось Оу, направленную вверх. Тогда запишем закон изменения импульса в проекции на эту ось:
$F_{ср} t=p_{2y}-p_{1y}$, где $p_{2y}$ и $p_{1y}$ - проекции импульсов на ось Оу после удара и до него соответственно
Так как импульс до удара направлен вниз, то его проекция на Оу будет отрицательной. Отсюда:
$F_{ср} t=p_{2}+p_{1}=mv_{2}+mv_{1}$, т.е. ${t=m(v_{2}+v_{1})/F_{ср}=0,036 с}$
Ответ: 0,036 с
Обоснование:
1) Будем считать систему отсчёта, связанную с Землёй, инерциальной
2) Так как сопротивление воздуха пренебрежимо мало, то при падении шара до удара его полная механическая энергия сохраняется. Можем использовать закон сохранения энергии (ЗСЭ)
3) При ударе импульс тела не сохраняется, поэтому воспользуемся законом изменения импульса. При этом внешней силой здесь является только средняя сила удара, так как по условию действием силы тяжести можно пренебречь
Задача 2
Шарик , висящий на нити длиной 2 м, отводят в сторону так, чтобы нить заняла горизонтальное положение, и отпускают без толчка. Внизу на расстоянии 1,5 м под точкой подвеса вбит гвоздь. В момент, когда она вновь займёт горизонтальное положение, налетев на гвоздь, сила её натяжения будет равна 15 Н. Определите массу груза
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Обоснование:
1) для всего движения шара выполняется закон сохранения энергии маятника, так как неконсерватиыне силы (силы трения) отсутствуют, а силой сопротивления воздуха можно пренебречь
2) Сила натяжения нити всегда направлена к центру окружности, по дуге которой движется груз маятника. Значит сила натяжения нити является центростремительной силой и в любой момент времени задаёт центростремительную составляющую ускорения груза: $a_ц={υ^2}/{r}$
Дано:
$T=15$Н
$l=2$м
$h=1,5$м
Решение:
В момент, когда нижняя часть нити займет горизонтальное положение, шарик будет на той же высоте, что и гвоздь. Тогда по закону сохранения энергии $mgh={mυ^2}/{2}$ (1), где $h$ - расстояние между гвоздём и точкой подвеса маятника. (Высоту гвоздя берём за 0 потенциальной энергии, поэтому вся потенциальная энергия переходит в кинетическую). Сила натяжения есть центростремительная сила, и она задаёт центростремительную составляющую $a_ц$ ускорения груза $a↖{→}$.
Второй закон Ньютона для груза, когда нить приняла горизонтальное положение, налетев на гвоздь: $T↖{→}+mg↖{→}=ma↖{→}$.
В проекции на горизонтальную ось, направленную вдоль нити в сторону гвоздя: $T=ma_ц=m{υ^2}/{r}$ (2),
$r=l-h=2-1,5=0.5$м - длина части нити, которая ниже гвоздя.
Из (1) следует, что ${υ^2}=2gh$, тогда $m={Tr}/{2gh}={15·0,5}/{2·10·1,5}=0,25$кг
Задача 3
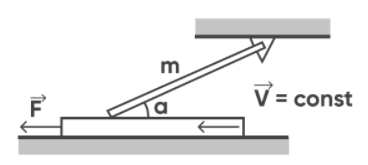
Однородный тонкий стержень массой m = 1 кг одной стороной прикреплён к потолку с помощью шарнира, а другой опирается на тяжелую горизонтальную доску, образуя с ней угол α = 30°. Под действием горизонтальной силы F доска движется поступательно влево с постоянной скоростью V (см. рисунок). Стержень при этом неподвижен. коэффициент трения стержня по доске μ = 0,2. Трением доски по опоре и трением в шарнире пренебречь.
Найдите F.
Какие законы Вы использовали для описания движения тела? Обоснуйте их применимость к данному случаю.
Решение
Обоснование:
1) В инерциальной системе отсчёта , связанной с Землёй, доска движется поступательно с постоянной скоростью. Поэтому сумма проекций на ось Ох и Оу всех сил, приложенных к доске, равна нулю.
2)В инерциальной системе отсчёта стержень покоится, так как отсутствует вращательное движение, для стержня выполняется условие равновесия: сумма моментов сил, действующих на стержень, относительно любой оси равна нулю.
Решение:
Fтр$_1$-F=0 (Силы, действующие на доску, Fтр$_1$ - сила трения со стороны пола).
По 3-ему закону Ньютона : Fтр$_1$ = Fтр$_2$=F (Fтр$_2$ - сила трения между стержнем и доской, направлена влево)
По условию задачи стержень покоится, значит сумма моментов сил равна нулю. Обозначим его длину - L и запишем это условие: $(mgLcosα)/2$ = Fтр$_2$Lsinα+NLcosα (Уравнение моментов записано относительно верхней точки стержня , чтобы занулить силы со стороны шарнира)
Fтр$_2$ = KN => $(mgLcosα)/2$ =KNLsinα+NLcosα
N= $(mg)/2(1+Ktgα)$.
F=KN=K $(mg)/2(1+Ktgα)$ = 0.9 Н
Задача 4
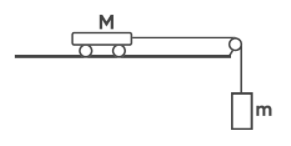
Тачка массой M = 0.9 кг связана невесомой и нерастяжимой нитью с грузом массой m. Если тачку толкнуть влево, то она будет двигаться с ускорением 2 м/с$^2$, если толкнуть вправо, то её скорость будет постоянной. Найти массу груза m.
Какие законы вы использовали? Обоснуйте применимость этих законов.
Решение
Пояснение: В горизонтальном направлении на тачку действуют сила трения (Fтр)и сила натяжения нити(Т). В первом случае они обе направлены против движения, тачка движется равнозамедленно. Во втором случае силы направлены в разные стороны и компенсируют друг друга, поэтому тачка движется равномерно. Так как нить нерастяжима, тачка и груз двигаются с одинаковым ускорением a. Так как нить невесома, силы натяжения нити, действующие на тачку и на груз будут равны по модулю: при движении с ускорением $T_1$, при движении равномерно $T_2$. Выберем систему отсчёта, связанную со столом, эту систему будем считать инерциальной. Тела в системе двигаются поступательно, поэтому их можно рассматривать как материальные точки. Для описания системы можем использовать 2 закон Ньютона. Запишем его для тачки и для груза для обоих случаев в проекцииях на горизонтальную и вертикальные оси.
Решение :
2 закон Ньютона для тачки в проекции на горизонтальную ось:
Ma=Fтр+Т$_1$ (1) - в 1 случае
0=Т$_2$-Fтр (2) - во втором случае
2 закон Ньютона для груза в проекции на вертикальную ось: :
ma=mg-T$_1$ (3) - в 1 случае
0=mg-T$_2$ (4) - во втором случае
Решим систему уравнений (1)-(4)
< Ma+ma=2mg => $m=(Ma)/(2g-a) = (0.9*2)/(2*10-2)$ = 0.1кг=100г
Задача 5
Шарик массой 200 г, висящий на нити длиной 1,5 м, отводят в сторону так, чтобы нить заняла горизонтальное положение, и отпускают без толчка. Внизу на расстоянии 1,0 м под точкой подвеса вбит гвоздь. Какую силу натяжения будет иметь нить в момент, когда она вновь займёт горизонтальное положение, налетев на гвоздь?
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Обоснование:
1) для всего движения шара выполняется закон сохранения энергии маятника, так как неконсерватиыне силы (силы трения) отсутствуют, а силой сопротивления воздуха можно пренебречь
2) Сила натяжения нити всегда направлена к центру окружности, по дуге которой движется груз маятника. Значит сила натяжения нити является центростремительной силой и в любой момент времени задаёт центростремительную составляющую ускорения груза: $a_ц={υ^2}/{r}$
Дано:
$m=200г=0.2$кг
$l=1.5$м
$h=1$м
Решение:
В момент, когда нижняя часть нити займет горизонтальное положение, шарик будет на той же высоте, что и гвоздь. Тогда по закону сохранения энергии $mgh={mυ^2}/{2}$ (1), где $h$ - расстояние между гвоздём и точкой подвеса маятника. (Высоту гвоздя берём за 0 потенциальной энергии, поэтому вся потенциальная энергия переходит в кинетическую). Искомая сила натяжения есть центростремительная сила, и она задаёт центростремительную составляющую $a_ц$ ускорения груза $a↖{→}$.
Второй закон Ньютона для груза: $T↖{→}+mg↖{→}=ma↖{→}$.
В проекции на горизонтальную ось, направленную в сторону гвоздя: $T=ma_ц=m{υ^2}/{r}$ (2),
$r=l-h=1.5-1=0.5$м - длина части нити, которая ниже гвоздя.
Из (1) следует, что ${υ^2}=2gh$, тогда $T={m2gh}/r={0.2·2·10·1}/0.5=8H$
Задача 6
С горки высотой 10 м, расположенной под углом 30◦ к горизонту, скатывается мальчик на санках. Какое расстояние проедут санки по горизонтальной поверхности после скатывания с горки, если коэффициент трения на всём пути 0,05? Ответ округлите до десятых
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Обоснование:
1) рассмотрим систему отсчёта, завязанную с землёй, это инерциальная система отсчёта, значит в данной задаче применим 2 закон Ньютона
2) для движения саней справедлив закон изменения энергии, так как присутствует непотенциальная сила - сила трения-скольжения. Работа силы трения равна изменению полной механической энергии саней
Дано:
$h=10$м
$μ=0.05$
$α=30°$
$g=10м/с^2$
$S_2-?$
Решение:
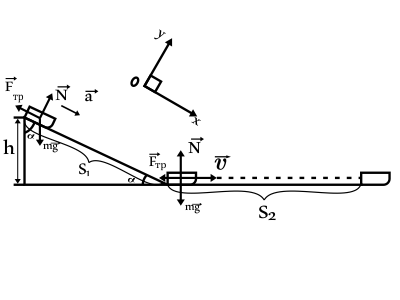
1 способ: через закон изменения энергии
Сумма работ сил трения на участках $S_1$ и $S_2$ равна изменению полной механической энергии мальчика на санках:
$∆E=A_{тр1}+A_{тр2}$
$0-mgh=F_{тр1}S_1cos(a_1)+F_{тр2}S_2cos(a_2)$
$a_1$ $a_2$ - углы между силами трения и перемещениями. $a_1=a_2=180$
$-mgh=-F_{тр1}S_1-F_{тр2}S_2$
$mgh=F_{тр1}S_1+F_{тр2}S_2$ (1)
Найдём силы трения:
2 закон Ньютона при движении по склону: $ma↖{→}_1=mg↖{→}+F_{тр}↖{→}_1+N↖{→}_1$
Проекция на ось, перпендикулярную наклонной поверхности: $N_1-mgcosα=0$ $=>$ $N_1=mgcosα$
Путь, пройденный санками по горе $S_1$ равен: $S_1={h}/{sinα}$
$F_{тр1}=μN_1=μmgcosα$
2 закон Ньютона при движении по горизонтальной поверхности: $ma↖{→}_2=mg↖{→}+F_{тр}↖{→}_2+N↖{→}_2$
Проекция на вертикальную ось: $N_2-mg=0$ $=>$ $N_2=mg$
$F_{тр2}=μN_2=μmg$
Подставим всё в уравнение (1):
$mgh=μmgcosα{h}/{sinα}+μmgS_2$ $h=μcosα{h}/{sinα}+μS_2$ $h-μctgα{h}=μS_2$ $S_2=h/μ(1-μctgα)=182.6$
***
2 способ: через кинематику
Запишем второй закон Ньютона: $ma↖{→}=mg↖{→}+F_{тр}↖{→}+N↖{→}$(1). В проекциях на Ох: $ma=mgsinα-F_{тр}$(2), Oy: $O=N-mgcosα$(3), откуда $N=mgcosα$(4). Учитывая, что сила трения $F_{тр}=μN=μmgcosα$(5). Тогда ускорение тела из (2): $a={mgsinα-F_{тр}}/{m}={mgsinα-μmgcosα}/{m}=g(sinα-μcosα)$(6). Путь, пройденный санками по горе $S_1$ равен: $S_1={h}/{sinα}={υ^2}/{2a}$. Откуда квадрат скорости в конце спуска: $υ^2={2ah}/{sinα}={2gh(sinα-μcosα)}/{sinα}=2gh(1-μctgα)$(7). Запишем закон сохранения энергии: ${mυ^2}/{2}-0=F_{тр}·S_2$. Откуда $S_2={mυ^2}/{2F_{тр}}$(8), где $F_{тр}=μmg$. Тогда расстояние, которое санки пройдут по горизонтальному участку до полной остановки: $S_2={mυ^2}/{2F_{тр}}={m·2gh(1-μctgα)}/{2μmg}={h}/{μ}(1-μctgα)$(9).
Подставим числовые значения и найдем $S_2$: $S_2={10}/{0.05}·(1-0.05·ctg30)=200·(1-0.05·√3)=200(1-0.0866)=200(0.91339)=182.679=182.7$м.
Задача 7
Небольшой шарик, падая с высоты 1 м, отскакивает от земли со скоростью в 0,94 раза меньшей, чем до удара. Определите, сколько ударов совершит шарик за 1,3 с.
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Обоснование: для полёта шара применим закон сохранения энергии, так как в системе отсутствуют непотенциальные силы (силой сопротивления воздуха пренебрегаем). При ударе шара о землю энергия не сохраняется, так как уменьшение скорости при ударе свидетельствует о потери кинетической энергии, значит удар нельзя считать упругим.
Дано:
$h_1=1$м
$υ_2=0.94υ_1$
$t=1.3$
$N-?$
Решение:
Падая с высоты $h_1$, шарик подлетает к полу со скоростью $υ_1$, а отталкивает от него со скоростью $υ_2=0.94υ_1$. Согласно закону сохранения механической энергии: $mgh_1={mυ_1^2}/{2}$ и $mgh_2={mυ_2^2}/{2}$, откуда $υ_1=√{2gh_1}$, а $υ_2=√{2gh_2}$
После почленного деления получим: ${υ_2}/{υ_1}={0.94υ_1}/{υ_1}={√{h_2}}/{√{h_1}}$, т.е. $h_2=(0.94)^2·h_1$.
Промежуток времени с момента падения шарика до второго удара об пол: $t=t_1+2t_2$, где $t_1$ - время падения шарика с высоты $h_1$ и $t_2$ - время падения шарика с высоты $h_2$.
Найдем $t_1$ и $t_2$: $h_1={gt_1^2}/{2}$, откуда $t_1=√{{2h_1}/{g}}=√{{2·1}/{9.8}}=0.451c$. Тогда $t_2=√{{2h_2}/{g}}=0.94√{{2h_1}/{g}}=0.94·0.451c=0.4246c$
Поскольку после первого удара шарику нужно подняться на высоту $h_2$, то время между первым и вторым ударом будет равно $2t_2$ или $2t_2=2·0.4246=0.849c$
Сложив $t_1$ и $2t_2$ получим: $t_1=2t_2=0.451+0.849=1.3c$. Значит, за время $t=1.3$ секунды, шарик совершает $N=2$удара.
Задача 8
Тело брошено вертикально вверх с начальной скоростью v0 = 3,13 м/с. Когда оно достигло верхней точки полёта, из того же места с такой же скоростью бросили второе тело. Определите, на каком расстоянии от точки бросания встретятся тела. Сопротивление воздуха не учитывать. Ответ округлить до десятых
Какие законы Вы используете для описания характера изменения энергии тела? Обоснуйте их применимость к данному случаю.
Решение
Дано:
$υ_0=3.13м/c$
$h-?$
Решение:
Запишем уравнения движения для 1 и 2 тела $\{\table\y=υ_0t_1-{gt_1^2}/{2}; \y=υ_0t_2-{gt_2^2}/{2};$
Также известно, что 2 тело бросили позднее по $t_1-t_2=τ$,
$τ$-время, за которое первое тело долетело до верхней точки.
В верхней точке $v=0=v_0-gτ$, значит $τ={υ_0}/{g}$.
$y=h$ - высота, на которой тела встретились.
Решим систему уравнений: (здесь представлено одно из множества возможных решений системы уравнений)
$\{\table\h=υ_0t_1-{gt_1^2}/{2}; \h=υ_0t_2-{gt_2^2}/{2};$
Вычитаем из верхнего уравнения нижнее:
$v_0(t_1-t_2)-g/2({t_1}^2-{t_2}^2)=0$
$v_0(t_1-t_2)-g/2(t_1-t_2)(t_1+t_2)=0$
$v_0-g/2(t_1+t_2)=0$
$v_0=g/2(t_2+τ+t_2)=g/2(2t_2+{υ_0}/{g})$ (учтено, что $t_1=t_2+τ$ и что $τ={υ_0}/{g}$)
$t_2={υ_0}/{2g}$
Подставим $t_2$ во второй уравнение: $h=υ_0{υ_0}/{2g}-{g/{2}({υ_0}/{2g})^2}={{υ_0}^2}/{2g}-1/{4}{{υ_0}^2}/{2g}={3}/{4}·{υ_0^2}/{2g}={3}/{4}·{{3.13}^2}/{2·10}≈0.4$м.
Задача 9
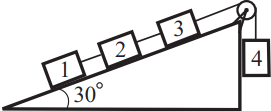
Три одинаковых груза массами 2 кг каждый соединены нитью, перекинутой через блок так, как показано на рисунке 320. Масса груза 4 равна 5 кг. Определите ускорение системы грузов, если коэффициент трения грузов о плоскость 0,1, а плоскость составляет с горизонтом угол 30◦. Нити невесомые, нерастяжимые. Ответ округлить до сотых.
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Обоснование: в данной задаче применим 2 закон Ньютона, так как каждый груз движется поступательно в инерциальной системе отсчёта. При этом, так как грузы соединены нерастяжимыми нитями, грузы будут двигаться с одинаковым ускорением. Силы натяжения каждой отдельно вязтой нити буут равны, так как нити невесомы.
Дано:
$m_1=m_2=m_3=m=2$кг
$m_4=5$кг
$μ=0.1$
$g=10м/с^2$
$a-?$
Решение:
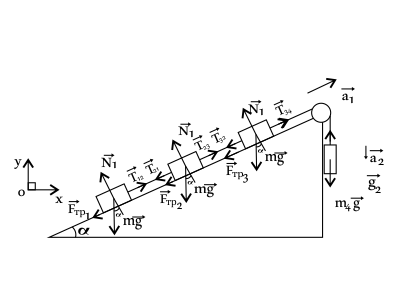
Учитывая, что нити невесомые и не растяжимые, то ускорения ${a_1}↖{→}={a_2}↖{→}={a}↖{→}$ и силы натяжения нитей: $T_{12}=T_{21};T_{23}=T_{32};T_{34}=T_{43}$(1).
Запишем второй закон Ньютона для каждого груза:
1 груз: $Ох_1$: $ma=T_{12}-mgsinα-F_{тр_1}$, где $F_{тр_1}=μN_1$; $Oy_1$: $O=N_1-mgcosα$, откуда $N_1=mgcosα; ma=T_{12}-mgsinα-μmgcosα$(2).
2 груз: $Ох_1$: $ma=T_{23}-T_{21}-mgsinα-μmgcosα$(3); $Oy_1$: $O=N_2-mgcosα$, откуда $F_{тр_2}=μN_2=mgcosα$.
3 груз: $Ох_1$: $ma=T_{34}-T_{32}-mgsinα-μmgcosα$(4); $Oy_1$: $O=N_3-mgcosα$, откуда $F_{тр_3}=μN_3=mgcosα$.
4 груз: $Oy_2$: $m_4a=m_4g-T_{43}$(5).
Из (2) выразим $T_{12}$: $T_{12}=ma+mgsinα+μmgcosα$(6).
Подставим (6) в (3), учитывая, что $T_{12}=T_{21}$: $ma=T_{23}-ma-mgsinα-μmgcosα-mgsinα-μmgcosα; T_{23}=2ma+2mgsinα+2μmgcosα$(7).
Подставим (7) в (4), учитывая, что $T_{23}=T_{32}$: $ma=T_{34}-2ma-2mgsinα-2μmgcosα-mgsinα-μmgcosα; T_{34}=3ma+3mgsinα+3μmgcosα$(8).
Подставим (8) в (5), учитывая, что $T_{34}=T_{43}$: $m_4a=m_4g-3ma-3mgsinα-3μmgcosα; m_4a+3ma=m_4g-3mgsinα-3μmgcosα$.
$a(m_4+3m)=m_4g-3mgsinα-3μmgcosα$
$a={m_4g-3mgsinα-3μmgcosα}/{(m_4+3m)}$(9)
Подставим числовые значения в (9) и найдем ускорение $a$: $a={5·10-3·2·10·0.5-3·0.1·2·10·0.866}/{5+3·2}={50-30-5.196}/{11}={14.804}/{11}=1.345м/с^2≈1.35м/с^2$.
Задача 10
Два шара массами 0,3 кг и 0,2 кг находятся на двух нитях, подвешенных в одной точке. Большой шар отклонили на угол 60◦ и отпустили. На какой максимальный угол отклонятся от вертикали оба шара, если соударение шаров абсолютно неупругое?
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Обоснование:
1) для отдельно рассматриваемых движений: движения шара до удара и движения двух шаров после удара - применим закон сохранения полной механической энергии, так как отсутствуют непотенциальные силы (силой сопротивления воздуха пренебрегаем)
2) при абсолютно неупругом ударе шаров энергия системы не сохраняется, но выполняется закон сохранения импульса системы, так как время взаимодействия шаров мало .
Дано:
$m_1=0.3$кг
$m_2=0.2$кг
$α=60°$
$β-?$
Решение:
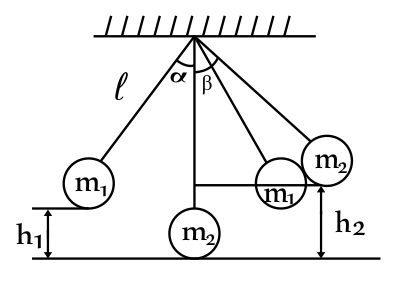
Запишем закон сохранения энергии: $W_{п_1}=W_{к_1}$ или $m_1gh_1={m_1υ_1^2}/{2}$(2), где $h_1=l(1-cosα)$, где $l$ - длина нити. Тогда скорость первого шара перед ударом: $υ_1=√{2gl(1-cosα)}$(3). Запишем закон сохранения импульса: импульс системы остается постоянным при любых взаимодействиях внутри системы: $m_1υ_1↖{→}=(m_1+m_2)·U↖{→}$(4). В проекции на ось $X$: $m_1υ_1=(m_1+m_2)·U$(5). Тогда скорость шаров после соударения: $U={m_1υ_1}/{(m_1+m_2)}$(6). Запишем закон сохранения энергии: $W'_{к_1}=W'_{п_1}$ или ${m_1U^2}/{2}=m_1gh_2$, где $h_2=l(1-cosβ)$(7). Тогда высота $h_2$, на которую поднимутся шары после удара: $h_2={U^2}/{2g}={1}/{2g}·{m_1^2}/{(m_1+m_2)^2}·υ_1^2={1}/{2g}·{m_1^2·2gh_1}/{(m_1+m_2)^2}$ или $l-lcosβ={m_1^2·(l-l·cosα)}/{(m_1+m_2)^2}⇒l(1-cosβ)={0.09·l(1-cosα)}/{0.25}⇒0.25-0.25cosβ=0.09-0.09cosα⇒0.25-0.25cosβ=0.09-0.09cos60°⇒0.25-0.25cosβ=0.09-0.09·0.5$
$0.25cosβ=0.25-0.09+0.045$
$0.25cosβ=0.205$
$cosβ={0.205}/{0.25}=0.82$
$β=arccos(0.82)$
$β=34.91°$
Задача 11
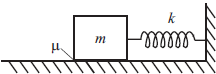
К одному концу лёгкой пружины прикреплён груз массой $m = 1$ кг, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно. Коэффициент трения груза на плоскости $μ = 0.2$. Груз смещают по горизонтали, растягивая пружину, затем опускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно $d = 15$ см. Найдите жёсткость $k$ пружины.
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
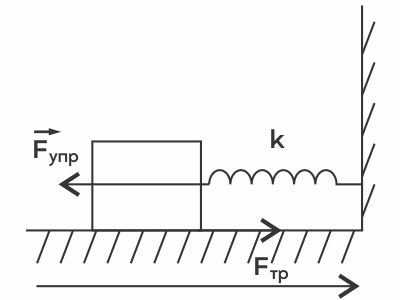
Обоснование:
1)так как в системе есть сила трения, энергия пружинного маятника не сохраняется. Значит работает закон изменения энергии, согласно которому работа силы трения равна изменению полной механической энергии
2) рассматривая задачу в системам отсчёта, связанной с неподвижной плоскостью, можем применять второй закон Ньютона
Закон изменения энергии: $E_{п2}-E_{п1}=A_{F_{тр}}$, где $A_{F_{тр}}$ - работа силы трения
Потенциальные энергии для начального и конечного положений: $E_{п1}={kd^2}/{2}; E_{п2}={Kx^2}/{2}$
Работа силы трения по перемещению груза из первого положения во второе: $A_{F_{тр}}=-μmg(d+x)$
Проекция второго закона Ньютона на ось х во втором положении: $μmg=kx⇒x={μmg}/{k}$ - подставим в закон изменения энергии, используя выражение для работы силы трения и потенциальной энергии пружины:
$${Kx^2}/{2}-{kd^2}/{2}=-μmg(d+x)$$ так как $=x={μmg}/{k}$, то при подстановке получим следующее: $${K({{μmg}/{k}})^2}/{2}-{kd^2}/{2}=-μmg(d+{μmg}/{k})$$ раскроем скобки: $${(μmg)^2}/{2k}-{kd^2}/{2}=-μmgd-{(μmg)^2}/{k}$$ приведём подобные слагаемые: $${3}/{2} {(μmg)^2}/{k} - {kd^2}/{2}+μmgd =0$$ приведём к общему знаменателю: $$3(μmg)^2-k^2 d^2+2μmgd k =0$$ Преобразуем и получим квадратное уравнение относительно $k$
$k^2-{2μmg}/{d}k-3{μ^2m^2g^2}/{d^2}=0$
$k={μmg}/{d}±√{4{μ^2m^2g^2}/{d^2}}={μmg}/{d}±2{μmg}/{d}$
Выберем положительное значение: $k={3μmg}/{d}=40$Н/м
Задача 12
Пуля, летящая горизонтально со скоростью 80 м/с, пробивает шар, висящий на невесомой нити, и вылетает со скоростью 60 м/с. Масса шара в 4 раза больше массы пули. Найдите, чему равна длина нити, если после удара шар отклонился на 60$°$ от вертикали.
Какие законы физики Вы используете для решения задачи? Обоснуйте их применимость к данному случаю.
Решение
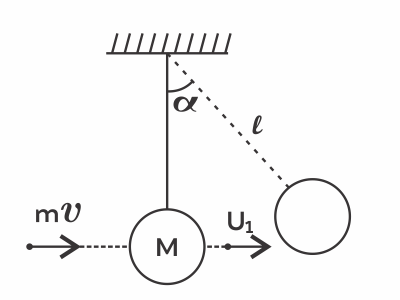
Пусть $v$ - скорость пули до соударения с шаром, $v_1$ - скорость после соударения, $U$ - скорость шара после соударения. По ЗСИ: $mv=MU+mv$
откуда $U={m}/{M}(v-v_1)$
Запишемт ЗСЭ для шара ${MU^2}/{2}=Mgh$, где $h$ - высота подъема шара.
$h=l(1-cosα)$
$U^2=2gl(1-cosα), U=-(v-v_1)={v-v_1}/{4}$
${(v-v_1)^2}/{16·2g(1-cosα)}=l$
$l={(80-20)^2}/{32·10·(1-cos60)}={400}/{160}=2.5$м
Задача 13
Из пушки вертикально вверх выпущен снаряд с начальной скоростью 400 м/с. В точке максимального подъёма снаряд разорвался на два осколка. Первый упал на землю вблизи точки выстрела, имея скорость в 2 раза больше начальной скорости снаряда, а второй в этом же месте — через 1 мин 40 с после разрыва. Чему равно отношение массы первого осколка к массе второго осколка? Сопротивлением воздуха пренебречь. Ответ округлите до десятых.
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Обоснование:
1) так как по условию задачи разрешено пренебречь сопротивлением воздуха, в процессе подъёма до точки разрыва на снаряд не действуют никакие непотенциальные силы, поэтому применим закон сохранения энергии
2) в процессе разрыва снаряда выполняется закон сохранения импульса, так как время разрыва мало
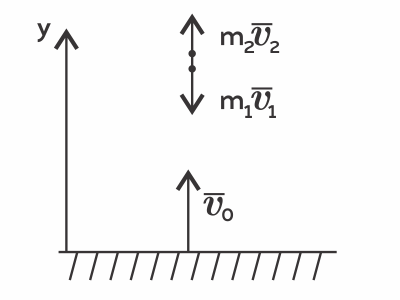
1) Точка максимального подъема: $h={v_0^2}/{2g}$
2) В точке максимального подъема в момент разрыва выполняется закон сохранения импульса в проекции на ось у: $m_1v_1=m_2v_2⇒{m_1}/{m_2}={v_2}/{v_1}$
3) Для первого осколка: $h={v_k^2-v_1^2}/{2g}⇒v_1^2=v_k^2-v_0^2(v_0^2=2gh)$
4) Для второго осколка: $0=h+v_2τ-{gτ^2}/{2}⇒v_2={gτ}/{2}-{h}/{τ}$
Соответственно получаем: ${m_1}/{m_2}={({gτ}/{2}-{h}/{τ})}/{√{v_k^2-v_0^2}}≈0.6$
Задача 14
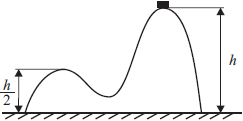
Горка с двумя вершинами, высоты которых $h$ и ${1}/{2} h$, покоится на гладкой горизонтальной поверхности стола. На правой вершине горки находится монета. От незначительного толчка монета и горка при- ходят в движение, причём монета движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. В некоторый момент времени монета оказалась на левой вершине горки, имея скорость $ν$. Найдите скорость горки в этот момент.
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Обоснование:
1) для системы горка-монета применим закон сохранения импульса, так как внешние силы, действующие на систему скомпенсированы (сила тяжести и сила реакции опоры) и систему можно считать замкнутой
2) полная механическая энергия монеты при движении по горке сохраняется, так как поверхность горки гладкая, а значит силы трения отсутствуют
Дано:
$h_1=h$
$h_2=h/2$
$v_m=v$
Решение:
Закон сохранения импульса системы горка+монета:
$Δp↖{→}=0$
$p↖{→}_1=p↖{→}_2$
Начальный импульс системы: $p_1=0$
$0=mv↖{→}_м+Mv↖{→}_г$
$m$ - масса монеты, $M$ - масса горки/
В проекциях на горизонтальную ось x, направленную вправо:
$0=-mv_м+Mv_г$ $=>$ $mv_м=Mv_г$ (2)
Закон сохранения полной механической энергии системы:
$ΔE=0$ $=>$ $E_2-E_1=0$
$E_1,E_2$ - полн. мех. энергия системы в состояниях, когда монета находится на правой и левой вершинах соответственно.
$mgh_1+{m{v_{м0}}^2}/2=mgh_2+{m{v_{м}}^2}/2+{М{v_{г}}^2}/2$ (2)
Таким образом, часть потенциальной энергии монеты переходит в кинетическую энергию горки и самой монеты
Начальная скорость монеты $v_{м0} =0$ по условию
Для того, чтобы найти скорость горки ${v_{г}}^2$ из уравнения (2):
${v_{г}}^2=m/M2g(h_1-h_2)-m/M{v_{м}}^2$
${v_{г}}^2=m/M(2g(h_1-h_2)-{v_{м}}^2)$
Dыразим соотношение масс $M/m$ из уравнения(1):
$M/m={v_{м}}/{v_{г}}$
Подставим это в выражение для ${v_{г}}^2$:
${v_{г}}^2={v_{г}}/{v_{м}}(2g(h_1-h_2)-{v_{м}}^2)$
Сократим ${v_{г}}$ и подставим значения высот, а также учтем, что $v_m=v$ :
${v_{г}}=1/{v}({2g(h-h/2)-{v^2}})={2gh/2}/v-v={gh}/{v}−v$
Ответ: ${gh}/{v}−v$
Задача 15
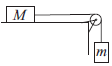
В системе, изображённой на рисунке, груз массой m = 0,5 кг начал двигаться вниз с ускорением 2 м/с2. Груз соединён с горизонтально лежащим бруском невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок. Найдите массу бруска M, если коэффициент трения бруска о поверхность стола равен 0,3. Ответ в кг.
Какие законы Вы используете для описания характера изменения энергии тела? Обоснуйте их применимость к данному случаю.
Решение
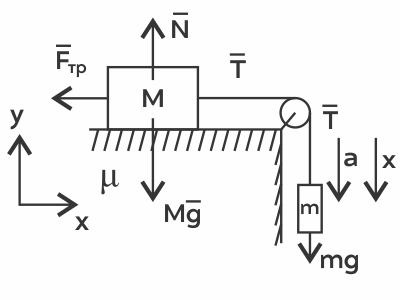
Расставим силы, действующие на тела. Т.к. тела связаны нитью, то они двигаются с одинаковым ускорением. Запишем II закон Ньютона для бруска и груза:
$\{\table\m{g}↖{-}+{T}↖{-}=m{a}↖{→}; \M{g}↖{-}+{N}↖{-}+{T}↖{→}+{F_{тр}}↖{-}=M{a}↖{-};$
в проекции на оси: $\{\table\T-F_{тр}=Ma; \N=Mg; \mg-T=ma;$ $F_{тр}=μMg$
Откуда $mg-μMg=Ma+ma$
$m(g-a)=M(a+μg)$
$M=m{g-a}/{a+μg}=0.8$кг
Задача 16
В верхнюю точку треугольного клина с длиной основания $L = 49$ см, углом наклона $α = 45°$ и массой $M = 300$ г поместили прямоугольный брус с основанием $l = 10$ см и массой $m = 50$ г. Брус отпускают, и он начинает свободно скользить по клину. Какое расстояние пройдёт клин к моменту, когда брус коснётся горизонтальной поверхности, на которой находится клин? (Силами трения бруса о клин и клина о горизонтальную поверхность пренебречь.)
Какой закон вы использовали для описания системы? Обоснуйте применимость этого закона.
Решение
Обоснование: в данной системе применим закон сохранения импульса в проекции на горизонтальную ось, так как проекция внешних сил, действующих на систему "брусок-клин", на горизонтальную ось равна нулю.
Введём систему координат, направив ось $Ox$ горизонтально (см. рис.). Обозначим $v_{1x}$ и $v_{2x}$ — проекции скоростей бруса и клина на ось $Ox$. Запишем закон сохранения импульса: $mv_{1x} + Mv_{2x} = 0 ⇒ {v_{1x}} / {v_{2x}} = -{M} / {m} = -6$ (1).
Горизонтальное перемещение бруска и клина пропорциональны скорости:
${S_{1x}}=v_{1x0}t+{a_{1x}t^2}/2$, начальная скорость $v_{1x0}=0$, ускорение $a_{1x}={v_{1x}-v_{1x0}}/t={v_{1x}/t$. Тогда ${S_{1x}}={v_{1x}t}/2$. Аналогично ${S_{2x}}={v_{2x}t}/2$.
Т.к. соотношение (1) справедливо для любого момента времени, то для перемещений клина и бруса можно записать ${S_{1x}} / {S_{2x}} = {v_{1x}t} / {v_{2x}t}=-6$, т.е. $S_{x1} = -6S_{x2}$.
Брусок коснётся горизонтальной поверхности, когда $S_{1x} = L - l\cosα - |S_{x_2}|$, следовательно, $-6S_{x2} = L - l\cosα + S_{x_2}$ (учтено, что $S_{x2}<0$)
Получаем ответ $S_{x2} = -{L - l\cosα} / {7} = -({49см - {10см} ⋅{√ {2}} / {2}}/ {7}) = -6$ см. Перемещение клина будет отрицательным, так как оно направлено против оси x. Клин переместится на расстояние $|S_{x2}|=6$ см
Задача 17
Из ствола безоткатного орудия, установленного на горизонтальной платформе, вылетает снаряд массой $20$ кг со скоростью $200$ м/с под углом $45°$ к горизонту. На какое расстояние откатится платформа с орудием, если их масса $2$ т, а коэффициент сопротивления движению платформы равен $0,\!1$?
Какие законы вы использовали для описания системы? Обоснуйте применимость этих законов.
Решение
Обоснование:
1) Систему "снаряд-платформа с орудием" можно считать замкнутой, так как действие внешних сил (сила тяжести и сила реакции опоры) скомпенсированы, значит для системы выполняется закон сохранения импульса.
2) Сила сопротивления движению платформы создаёт ускорение, под действием которого платформа тормозит
Дано
$m=20кг$
$v=200м/с$
$α=45°$
$μ=0,1$
$m_n=2000кг$
$S-?$
Анализ
$1)m·v·cos45=m_n·u$
$2)a={F}/{M}={K·M·g}/{M}=kg$
$3)S={at^2}/{2}$ или $2aS=u^2$
$S={u^2}/{2a}$
Решение
$u={m·v·cos45}/{m_n}$
$u={200·20·0,7}/{2000}=1.4м/с$
$a=0,1·10=1м/с^2$
$S={1.4^2}/{2·1}=0,98$ м $ м
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

