Задание 25. Электродинамика (расчетная задача высокого уровня). ЕГЭ 2026 по физике
Средний процент выполнения: 14.3%
Ответом к заданию 25 по физике может быть целое число или конечная десятичная дробь.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
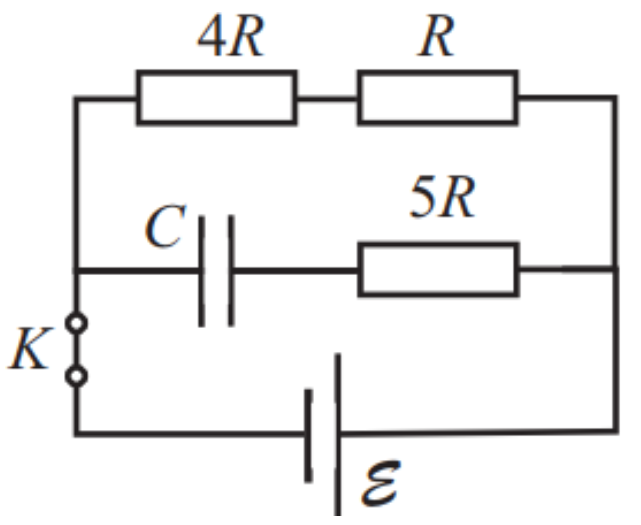
На рисунке приведена схема цепи с параметрами ε = 13 В, C = 10 мкФ, R = 5 Ом. Ключ уже долгое время находится в замкнутом положении. Чему равен заряд на конденсаторе? Внутреннее сопротивление источника тока r = 1 Ом.
Решение
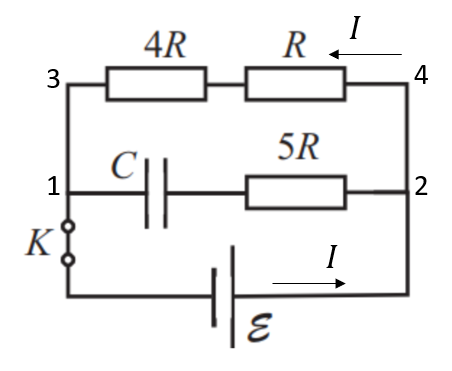
Заряд конденсатора: $q=CU_c$
Так как ключ длительное время находится в замкнутом положении, конденсатор полностью заряжен. Значит по участку цепи 12 ток не течёт, тогда напряжение на резисторе 5R равно нулю. Это следует из закона Ома:
$I_{5R}={U_{5R}}/{5R}$ => $U_{5R}=I_{5R}5R=0$, так ток через резистор $I_{5R}=0$.
Значит напряжение на участке цепи 12 $U_{12}=U_c+U_{5R}=U_c+0=U_c$
Так как участки 12 и 34 параллельны, то напряжения на них равны: $U_{12}=U_{34}$
Напряжение $U_{34}$ можно найти по закону Ома для участка цепи 34, по которому протекает полный ток цепи $I$:
$I={U_{34}}/{4R+R}$ => $U_{34}=I5R$
По закону Ома для замкнутой цепи: $I=ε/{5R+r}$
Объединяя все полученные выводы получим выражение для заряда конденсатора:
$q=CU_c=CU_{34}=Cε/{5R+r}5R=125$ мкКл
Задача 2
Электрон прошёл ускоряющую разность потенциалов 5 В. Какую скорость при этом приобрёл электрон, если его начальная скорость равна нулю. Ответ представьте в $10^6$ м/с и округлите до десятых.
Справочные данные: масса электрона $9.1⋅10^{-31}$ кг, модуль заряда электрона $1,6⋅10^{-19}$ Кл.
Решение
Если разность потенциалов $U$ ускоряющая, то работа поля $A=|q|U$ ($q$ - заряд электрона) равна увеличению кинетической энергии электрона: $E_к-E_{к0}=A$.
Кинетическая энергия после прохождения ускоряющей разности потенциалов: $E_к={mv^2}/2$, где $m$ - масса электрона, $v$ - скорость, которую приобрёл электрон.
Так как начальная скорость равна нулю, начальная кинетическая энергия тоже равна нулю: $E_{к0}=0$.
Из (1) получим ${mv^2}/2=qU$, тогда $v=√{{2qU}/m}=√{{2⋅1,6⋅10^{-19}⋅5}/{9.1⋅10^{-31}}}=1.3⋅10^6$ м/с
Задача 3
Частица, имеющая заряд 0,2 нКл, переместилась в однородном горизонтальном электрическом поле на расстояние 0,45 м по горизонтали за время 3 с. Какова масса частицы, если её начальная скорость равна нулю, а напряжённость электрического поля 500 В/м? Ответ выразить в (мг).
Решение
Дано:
$q=0.2$нКл
$S=0.45$м
$t=3$с
$E=500$В/м
$m-?$
Решение:
Рассмотрим 2-й закон Ньютона спроецированный на горизонтальную ось. На частицу действуют $F_{тяж}$ и $F_{эл}$;
Запишем 2-й закон Ньютона в проекции на горизонтальную ось:
тогда $qE=ma_{гор}; a_{гор}={q·E}/{m}$, перемещение по Ох определяется $S={a_{гор}·t^2}/{2}$
Преобразуем, получим: $m={q·E·t^2}/{2·S}={0.2·10^{-9}·500·3^2}/{2·0.45}=10^{-6}=1$мг.
Задача 4
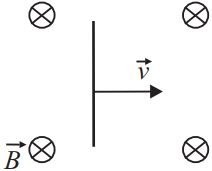
Горизонтально расположенный проводник движется равноускоренно в вертикальном однородном магнитном поле, индукция которого равна 0,5 Тл и направлена перпендикулярно проводнику и скорости его движения. При начальной скорости проводника равной нулю и ускорении 8 м/с2 проводник переместился на 1 м. ЭДС индукции на концах проводника в конце перемещения равна 2 В. Какова длина проводника? Ответ выразите в (м).
Решение
Дано:
$B=0.5Тл$
$υ_0=0м/c$
$a=8м/с^2$
$x=1м$
$ε=2B$
$l-?$
Решение: ЭДС индукции в проводнике, движущемся в однородном магнитном поле: $ε=-{∆Ф}/{∆t}$(1). Изменение магнитного потока за малое время $∆t: ∆Ф=B·∆S$(2), где площадь определяется как: $∆S=l·∆x$(3), тогда имеем: $∆Ф=B·l·∆x$(4). Следовательно, $|ε|={B·l·∆x}/{∆t}=B·l·υ$(5), где $υ$ - скорость движения проводника. В конце пути длиной $x$ скорость проводника $υ=√{2ax}$(6), где $a$ - ускорение так, что подставив (6) в (5), имеем: $|ε|=B·l·√{2ax}$(7), откуда длина проводника $l$ равна: $l={|ε|}/{B√{2ax}}$(8). $l={2B}/{0.5·√{2·8·1}}={2B}/{0.5·4}=1м$
Задача 5
Электрон прошёл ускоряющую разность потенциалов 100 В и влетел в однородное магнитное поле индукцией 5 · 10−4 Тл перпендикулярно сило вым линиям поля. Определите радиус траектории электрона в этом поле.Ответ дать в см.
Решение
Дано:
$U=100B$
$e=1.6·10^{-19}$Кл
$m_e=9.11·10^{-31}$кг
$B=5·10^{-4}$Tл
$α=90^o$
$R-?$
Решение:
Так как электрон влетел в однородное магнитное поле под прямым углом, то он будет двигаться по окружности радиуса $R$, где на него будут действовать сила Лоренца, которые будет задавать электрону центростремительное ускорение: $F_л=m_ea_{ц.с.}=eυB·sinα$, где $sinα=sin90=1$, $a_{ц.с.}={υ^2}/{R}; m_e{υ^2}/{R}=eυB$, откуда $R={m_eυ}/{eB}$(1). Скорость электрона $υ$ найдем из уравнения: $eU={m_eυ^2}/{2}$, откуда $υ=√{{2eU}/{m_e}}$(2), где $e$ - заряд электрона, $m$ - масса электрона.
Подставим (2) в (1): $R={m_e·√{{2eU}/{m_e}}}/{e·B}={√{2m_e·e·U}}/{e·B}={√{2m_e·U}·√{e}}/{√{e}·√{e}·B}={√{2m_e·U}}/{√{e}·B}={√{2·9.11·10^{-31}·100}}/{5·10^{-4}·√{1.6·10^{-19}}}={13.498·10^{-15}}/{20·10^{-4}·10^{-10}}=0.067=6.7$см.
Задача 6
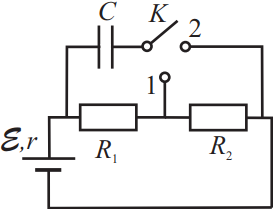
В электрической цепи, схема которой изображена на рисунке, конденсатор C изначально незаряжен. Ключ K переводят в положение 1. Затем, спустя длительное время, переключают его в положение 2 и снова ждут в течение достаточно большого промежутка времени. В результате перевода ключа в положение 2 энергия конденсатора увеличивается в n = 16 раз. Найдите сопротивление резистора R2, если R1 = 12 Ом.
Решение
Дано:
$A=25·10^3Дж$
$A′=20·10^3Дж$
${T_н}/{T_х}-?$
Решение:
Обозначим напряжение на конденсаторе после перевода ключа в положение 1 через $U_1$, а после перевода ключа в положение 2 — через $U_2$. Поскольку энергия $Е$ конденсатора, заряженного до напряжения $U$, равна $Е={CU^2}/{2}$, то отношение энергии конденсатора при положении ключа 2 к энергии конденсатора при положении ключа 1 равно $n={Е_2}/{E_1}={{CU_2^2}/{2}}/{{CU_1^2}/{2}}={U_2^2}/{U_1^2}$
Пусть сила тока, текущего через резисторы, равна $l$. При этом напряжения $U_1$ и $U_2$ на конденсаторе равны напряжениям на соответствующих участках цепи имеющих сопротивления $R_1$ и $R_1+R_2$. На основании закона Ома для участка цепи, получаем: $U_1=IR_1$ и $U_2=I(R_1+R_2)$.
Следовательно, $n={U_2^2}/{U_1^2}=({R_1+R_2}/{R_1})^2=(1+{R_2}/{R_1})^2$
Отсюда, $R_2 = (√n - 1)·R_1 = (4-1)·12Ом = 3·12 Ом = 36 Ом$.Задача 7
Электрон прошёл ускоряющую разность потенциалов 100 В и влетел в однородное электрическое поле напряжённостью 2·103 В/м в направлении силовых линий поля. Определите расстояние, которое электрон пролетел до остановки.
Решение
Дано:
$U=100B$
$e=1.6·10^{-19}$Кл
$E=2·10^3$В/м
$S-?$
Решение:
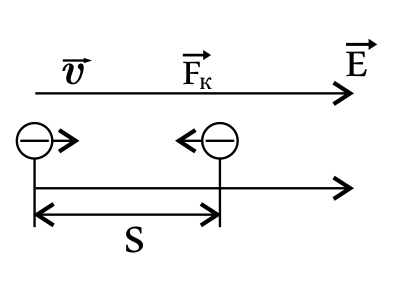
Если разность потенциалов $U$ ускоряющая, то работа ускоряющего электрон поля $A_1=|q|U$ ($q=e$ - заряд электрона) равна увеличению кинетической энергии электрона: $E_к-E_{к0}=A$.
Кинетическая энергия после прохождения ускоряющей разности потенциалов: $E_к={mv^2}/2$, где $m$ - масса электрона, $v$ - скорость, которую приобрёл электрон.
Так как начальная скорость равна нулю, начальная кинетическая энергия тоже равна нулю: $E_{к0}=0$.
Из (1) получим ${mv^2}/2=eU$
Когда электрон влетает в однородное электрическое поле, скорость его уменьшается до нуля, поскольку на него действует сила Кулона: $F_к=e·E$(2). Сила Кулона совершает работу: $A=-F_к·S$ (2), которая равна изменению энергии электрона $A=E_{к2}-E_к$ (3). Здесь $E_{к2}=0$ - конечная кинетическая энергия электрона (когда он остановился), $E_к={mv^2}/2$ - найденная ранее кинетическая энергия электрона после прохождения ускоряющей разности потенциалов.
Приравняв (2) и (3) получим: $-e·E·S=-{mv^2}/2$ (4).
Приравняв (1) и (4), получим: $eE·S=eU⇒S={U}/{E}$(3). Подставим числа: $S={100}/{2·1000}={1}/{20}=0.05м=5$см.
Задача 8
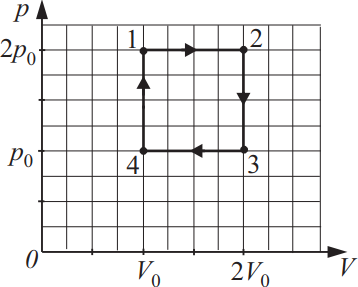
Какое количество теплоты рабочее вещество в цикле Карно отдаёт холодильнику, если количество теплоты, полученное от нагревателя, составляет 100 кДж? Температуры нагревателя и холодильника в рассматриваемом цикле Карно такие же, как максимальная и минимальная температуры цикла, изображённого на рисунке.
Решение
Дано:
$Q_н=10^5$Дж
$p_1=2p_0$
$V_1=V_0$
$p_2=2p_0$
$V_2=2V_0$
$p_3=p_0$
$V_3=2V_0$
$p_4=p_0$
$V_4=V_0$
$Q_x-?$
Решение:
КПД цикла Карно определяется выражением: $η=1-{Т_х}/{Т_н}$(1)
Из уравнения идеального газа $pV={m}/{μ}RT$(2), следует: ${p_1V_1}/{T_1}={p_2V_2}/{T_2}⇒{2p_0V_0}/{T_1}={2p_0V_0·2}/{T_2}⇒T_2=2T_1$(3)
${p_2V_2}/{T_2}={p_3V_3}/{T_3}⇒{2p_02V_0}/{T_2}={p_02V_0}/{T_3}⇒T_2=2T_3$(4)
Из уравнений (3) и (4) следует, что $T_1=T_3$(5)
${p_3V_3}/{T_3}={p_4V_4}/{T_4}⇒{p_02V_0}/{T_3}={p_0V_0}/{T_4}⇒T_3=2T_4$(6)
$T_2=2T_3=2·(2T_4)=4T_4$(7)
Таким образом, максимальная температура цикла - $T_н=Т_2$, минимальная - $T_х=Т_4$.
Тогда КПД $η=1-{Т_4/{Т_2}=1-{Q_х}/{Q_н}$, следовательно ${Q_х}/{Q_н}={Т_4/{Т_2}$;
${Q_х}={Т_4/{Т_2}{Q_н}=1/4{Q_н}=25$кДж
Задача 9
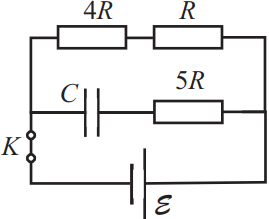
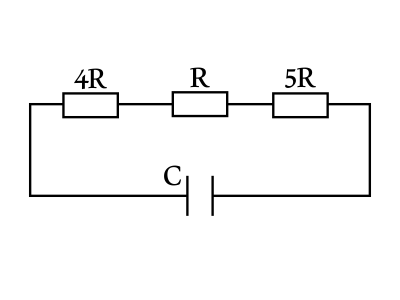
На рисунке приведена схема цепи с параметрами ε = 12 В, C = 10 мкФ, R = 5 Ом. Какое количество теплоты выделится на резисторе R после размыкания ключа K ? Внутренним сопротивлением источника пренебречь. Ответ укажите в $10^{-6}$ Дж
Решение
Дано:
$ε=12B$
$C=10^{-5}$ф
$R=5$Ом
$Q-?$
Решение:
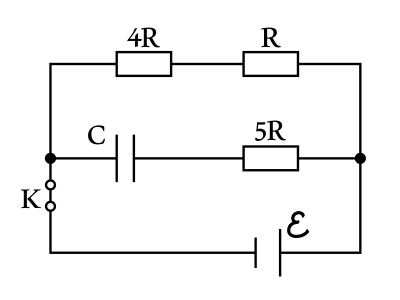
Электрический ток при замкнутом ключе К и заряженном конденсаторе через последовательно соединенные сопротивление 5R и конденсатор С не идет, поэтому напряжение на конденсаторе 5R $U_{5R}=0$. Конденсатор и резистор 5R параллельно соединены с последовательно соединенными резисторами 4R и R, поэтому для напряжений справедливо равенство: $U_c+U_{5R}=U_R+U_{4R}$. Выражая напряжения через закон Ома для участка цепи получим: $U_c=J·(R+4R)=5JR$(1).
По закону Ома для полной цепи ток равен: $J={ε}/{R+4R}={ε}/{5R}(2)$ (внутреннее сопротивление источника по условию пренебрежимо мало)
Подставим (2) в (1): $U_c={5·ε·R}/{5R}=ε=12B$(3).
Следовательно, пока ключ К замкнут, на пластинах конденсатора накапливается заряд и электрическая энергия: $W_э={CU_c^2}/{2}={cε^2}/{2}={10^{-5}·(12)^2}/{2}={144·10^{-5}}/{2}=72·10^{-5}$Дж(4).
После размыкания ключа К, вся энергия конденсатора выделится в виде тепла на последовательно соединенных резисторах $4R,R$ и $5R$, пропорционально их сопротивлениям: $W_э=(4+1+5)Q$
Откуда количество теплоты, выделяющееся на сопротивлении $R$ равно: $Q={W_э}/{10}={72·10^{-5}}/{10}=72·10^{-6}$Дж.
Задача 10
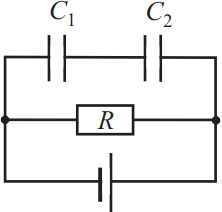
Два конденсатора с ёмкостями C1 = 250 пФ и C2 = 150 пФ включены в электрическую цепь, как показано на рисунке. ЭДС источника тока равна 6,2 В. Определите напряжение на конденсаторе C1, если известно, что при коротком замыкании цепи ток через источник возрастает в 3,7 раза.
Решение
Дано:
$С_1=250·10^{-12}$ф
$С_2=150·10^{-12}$ф
$ε=6.2$В
$n=3.7$
$U_1-?$
Решение:
Напряжение на резисторе, подключенном параллельно к конденсаторам: $U=U_1+U_2$(1), где $U_1$ и $U_2$ - напряжения на первом и втором конденсаторах соответственно. Конденсаторы соединены последовательно, следовательно, заряды на них будут одинаковыми: $q=C_1U_1=C_2U_2$(2). Решая совместно уравнения (1) и (2), получим: $U_1={C_2U_2}/{C_1}; U_2={C_1U_1}/{C_2}$
$U={C_2U_2}/{C_1}+U_2⇒U_2({C_2}/{C_1}+1)=U⇒U_2={U}/{({C_2}/{C_1}+1)}⇒U_2={U}/{{C_2+C_1}/{C_1}}⇒U_2={C_1U}/{C_1+C_2}$(3). Аналогично: $U=U_1+{C_1U_1}/{C_2}⇒U_1(1+{C_1}/{C_2})=U⇒U_1={U}/{(1+{C_1}/{C_2})}⇒U_1={U}/{{C_1+C_2}/{C_2}}⇒U_1={C_2U}/{C_1+C_2}$(4).
Через конденсаторы ток не идет, поэтому закон Ома для рассматриваемой цепи запишется в виде: $J={ε}/{R+r}$(5), где $r$ - внутреннее сопротивление источника; $J$ - сила тока, текущего через источник и резистор. Падение напряжения на резисторе, согласно закону Ома для однородного участка цепи: $U=J·R=ε-Jr$(6). Ток короткого замыкания соответствует условию $R=0$, т.е. $J_0={ε}/{r}$(7). Согласно условию задачи: ${J_0}/{J}=n=3.7$(8).
Подставляя (5) и (7) в выражение (8), имеем: ${ε}/{r}:{ε}/{(R+r)}=3.7⇒{ε}/{r}·{(R+r)}/{ε}=3.7⇒{R+r}/{r}=3.7⇒R=3.7r-r=2.7r$, т.е. $R=2.7r$(9). Подставляя (9) в (5), получим: $J={ε}/{2.7r+r}={ε}/{3.7r}$(10).
После подстановки силы тока $J$ в (6), получим: $U=ε-{ε·r}/{3.7·r}⇒U=ε-{ε}/{3.7}={3.7ε-ε}/{3.7}⇒U={2.7ε}/{3.7}={2.7·6.2}/{3.7}=4.524B$
Подставляя числовые значения в (4), имеем: $U_1={150·10^{-12}·4.524}/{400·10^{-12}}=1.6966≈1.7B$
Задача 11
Прямой проводник с током 2 А находится в однородном магнитном поле с индукцией 10 Тл. Угол между направлением тока в проводнике и линиями индукции магнитного поля равен 30◦. Определите активную длину проводника, если к нему приложена сила 2 Н. Ответ выразите в (м).
Решение
Дано:
$J=2A$
$B=10$Тл
$α=30°$
$F_A=2H$
$l-?$
Решение:
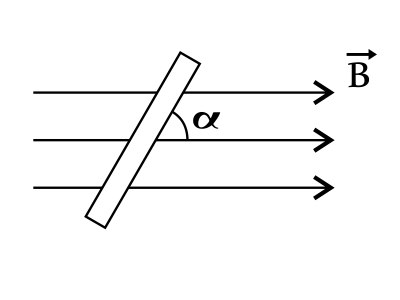
На проводнике с током в однородном магнитном поле действует сила Ампера: $F_A=J·B·l·sinα$(1), где $l$ - длина проводника. Выразим $l$ из (1): $l={F_A}/{J·B·sinα}$(2). Подставим числовые значения в (2): $l={2}/{2·10·sin30°}={1}/{10·0.5}={1}/{5}=0.2$м.
Задача 12
Под каким углом должен падать свет из воздуха на границу раздела воздух-стекло (n = 1,5), чтобы отражённый и преломлённый лучи были перпендикулярны друг другу? Ответ выразите в градусах и округлите до целых
Решение
Дано:
$n=1.5$
$γ=90°$
$φ-?$
Решение:
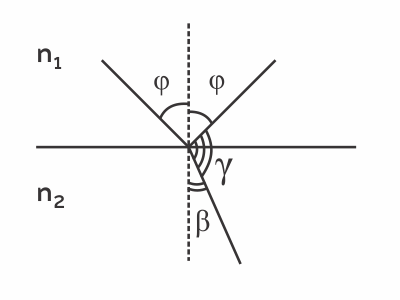
Закон преломления: $n_1sinφ=n_2sinβ$
$γ=180-φ-β=90°$, значит: $φ+β=90°$
$sinφ={n_2}/{n_1}cosφ, {n_2}/{n_1}=n$
$φ=arctgn=56°$
Задача 13
Конденсатор, заряженный до некоторого напряжения, соединяют разноимённо заряженными обкладками с конденсатором такой же ёмкости, но заряженным до напряжения, вдвое большего. Во сколько раз уменьшилась энергия системы после соединения конденсаторов?
Решение
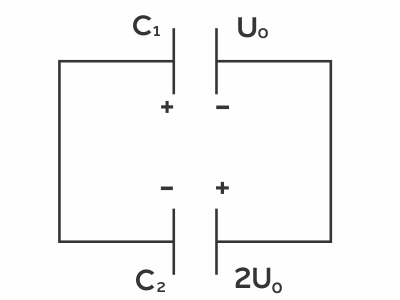
Заряд на первом конденсаторе: $q_1=C_1U_0$, на втором: $q_2=C_{1}2U_0=2q_1$
На левых обкладках конденсаторов суммарный заряд - $q$, значит, после установления равновесия на каждой, будет по - ${q}/{2}$. Аналогично, на правых будет по ${q}/{2}$. Энергия системы в начале:
$E_н={q^2}/{2C}+{4q^2}/{2C}={5q^2}/{2C}$
В конце: $E_k={q^2}/{4·2C}+{q^2}/{4·2C}={q^2}/{4C}$
Отношение: ${E_н}/{E_k}=10$
Задача 14
Свет от двух когерентных источников с длиной волны $λ$ образует на экране интерференционную картину в виде системы светлых и тёмных полос. Какова эта длина волны, если для двух соседних светлых полос разности хода для лучей, идущих от источников, равны 1,5 мкм и 2 мкм, соответственно? Ответ в мкм.
Решение
Условие максимума: $∆l=kλ, k∈Z$
$\{\table\∆l_1=kλ; \ ∆l_2=(k+1)λ;$ (так как максимумы соседние)
$k={∆l_1}/{λ}$
$∆l_2=({∆l_1}/{λ}+1)λ$
$∆l_2=∆l_1+λ⇒λ=∆l_2-∆l_1=0.5$мкм
Задача 15
Виток с током, равным 2 А, помещается во внешнее однородное магнитное поле, индукция которого равна 0,02 Тл, так, что плоскость контура перпендикулярна к направлению магнитного поля. Какую работу надо совершить, чтобы повернуть контур на 90$°$, если радиус витка равен 3 см? (Ответ в мДж, округлить до сотых)
Решение
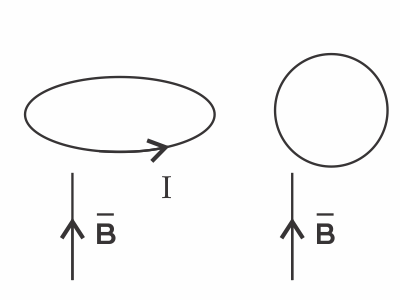
Работа внешних сил при повороте контура равна $A=-I∆Ф=-I(Ф_2-Ф_1)$, где $Ф_2$ - конечный поток, $Ф_1$ - начальный поток, пронизывающий контур.
$Ф=BS=B·πr^2$
$A=BI·πr^2=0.02·2·3.14·(0.03)^2≈1.1·10^{-4}$Дж = $0,11$мкДж
Задача 16

Маленький шарик с зарядом $q$ и массой $m$, подвешенный на невесомой нити с коэффициентом упругости $k$, находится между вертикальными пластинами плоского воздушного конденсатора. Расстояние между обкладками конденсатора $d$. Какова разность потенциалов между обкладками конденсатора, если удлинение нити $∆l$?
Решение
Задача 17
Однородную проволоку сопротивлением 160 Ом надо разрезать на два отрезка так, чтобы при соединении их параллельно можно было получить сопротивление 20 Ом. Найдите отношение длин отрезков проволоки? Ответ округлите до десятых.
Решение
Пусть сопротивление одного куска проволоки после разрезания равно х, тогда другого - 160-х. Они соединены параллельно:
${1}/{20}={1}/{x}+{1}/{160-x}$
${1}/{20}={160-x+x}/{(160-x)x}$
$x^2-160x+3200=0$
$x_{1,2}={160±√{160^2-4·3200}}/{2}≈23.5$(Ом)
Тогда сопротивление другого куска $160-x≈136.5$Ом.
Сопротивление проволоки пропорционально длине $R=ρ{l}/{S}$
Отношение длин равно отношению сопротивлений ${136.5}/{23.5}≈5.8$
Задача 18
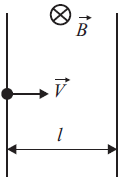
Первоначально покоившийся электрон проходит разность потенциалов 900 В и влетает в область магнитного поля шириной 5 мм. Скорость электрона в момент влёта перпендикулярна как линиям индукции поля, так и границам области. Под каким углом к границе области поля вылетит электрон, если индукция магнитного поля имеет величину 10 мТл?
Решение
Дано:
$U=900B$
$l=5$мм
$B=10$мТл
$q=-1.6·10^{-19}$ Кл
$m=9.1·10^{-31}$ кг
Найти:
$α-?$
Решение:
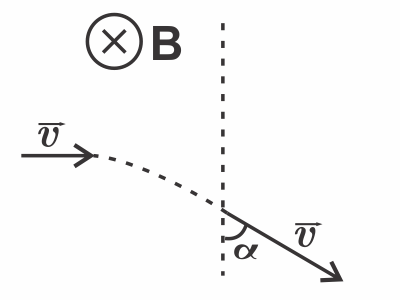
Сила Лоренца $F_л$ направлена перпендикулярно плоскости, содержащей вектора магнитной индукции $B↖{→}$ и скорости электрона $v↖{→}$. В любой момент времени, она всегда направлена к центру окружности, которую описывает электрон, и задаёт ему центростремительное ускорение $a_ц$:
Тогда, по 2 закону Ньютона $F_л=ma_ц$. Модуль $F_л=|q|Bvsinα'$, где $α'$ - угол между $B↖{→}$ и $v↖{→}$, по условию $α'=90^o$, значит $sinα'=1$;
2 закон Ньютона примет вид: $|q|Bv=m{v^2}/{R}⇒R={mv}/{|q|B}$ - радиус окружности, по дуге которой движется электрон.
Так как электрон был разогнан электрическим полем, приобретенная им кинетическая энергия равна работе поля: ${mv^2}/{2}=|q|U⇒v=√{{2|q|U}/{m}}$
Подставляя в уравнение для $R:R=√{{2mU}/{|q|}}·{1}/{B}=√{{2·9.1·10^{-31}·900}/{1.6·10^{-19}}}·10^2≈0,01$м.
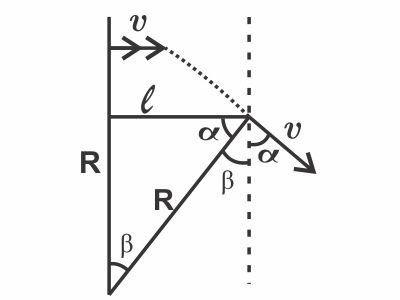
К моменту вылета из области действия поля, скорость электрона отклонится от первоначального направления на угол β, на такой же угол повернётся радиус-вектор электрона. Искомый угол: $α=90-β$, так как в начале электрон влетел перпендикулярно границе области.
Рассмотрим прямоугольный треугольник, образованный радиус-вектором при вылете, шириной области $l$ и левой границей области. Получим, что: $cosα={l}/{R}$
$cosα={0,005}/{0,01}=1/2⇒α=60°$
Задача 19
Электрон влетает в пространство между обкладками плоского горизонтально расположенного конденсатора параллельно его пластинам со скоростью 30 Мм/с. Напряжённость поля внутри конденсатора равна 3,5 кВ/м. На какое расстояние сместится электрон по вертикали при вылете из конденсатора, если длина его обкладок равна 10 см?
Решение
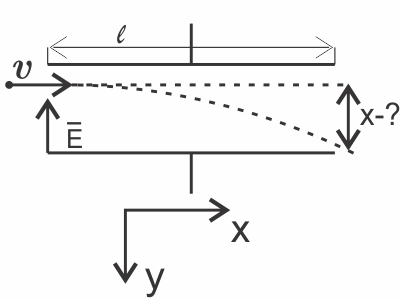
В проекции на ось Х на электрон никакие силы не действуют, следовательно, он двигается с постоянной скоростью. $v_x={l}/{t}$, где $t$ - время движения.
$v_x=v=3·10^7$м/с
$t={l}/{v}$
В проекции на ось у, на электрон со стороны поля действует сила $F=E·e$, где $l$ - заряд электрона. По действием этой силы электрон двигается равноускоренно $F=ma, x={at^2}/{2}, a={2x}/{t^2}$
$E·e={2mx}/{t^2}={2mxv^2}/{l}⇒x={Ee·l^2}/{2mv^2}$
$x={3.5·10^3·1.6·10^{-19}·0.1^2}/{2·9.1·10^{-31}·(3·10^7)^2}≈3.4·10^{-2}≈3,4$мм
Задача 20
Плоский воздушный конденсатор, расстояние между пластинами которого равно 0,5 мм, при разности потенциалов 500 В имеет заряд на пластинах 0,1 мкКл. Какова площадь обкладок конденсатора? Ответ выразите в квадратных дециметрах и округлите до десятых. Ответ в дм2.
Решение
Емкость плоского конденсатора $C={ε_0S}/{d}$. Связь между емкостью, зарядом и напряжением выражается формулой $q=CU$.
$q={ε_0S}/{d}U, S={qd}/{ε_0U}={0.1·10^{-6}·0.5·10^{-3}}/{8.85·10^{-12}·500}=0.011м^2$
$S=0.011м^2=1.1дм^2$
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

