Задание 4. Статика. Механические колебания и волны . ЕГЭ 2026 по физике
Средний процент выполнения: 70.5%
Ответом к заданию 4 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Алгоритм решения задания 4:
- Определи, какой физический процесс или явление рассматривается: равновесие тела, действие силы Архимеда, колебания или распространение волн.
- Выдели физическую модель, к которой относится ситуация: твёрдое тело, маятник или волновой процесс.
- Определи физические величины, описывающие данный процесс, и установи, какие из них заданы в условии.
- Соотнеси ситуацию с соответствующим законом или условием: условием равновесия, законом Архимеда, законом колебаний или соотношениями для волн и звука.
- Запиши применимый закон или формулу в общем виде, используя физические величины из условия.
- Выполни необходимые преобразования или вычисления в рамках выбранной физической модели.
- Проверь, что полученный результат согласуется с физическим смыслом рассматриваемого явления.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
В одно из колен сообщающихся сосудов налита вода, в другое — неизвестная жидкость. Высота столбика воды равна 8 см, а неизвестной жидкости - 10 см. Определите плотность неизвестной жидкости. Ответ дать в ${кг}/{м^3}$. Плотность воды 1000 ${кг}/{м^3}$.
Решение
${H_в}/{H}={ρ}/{ρ_в}$
$ρ={H_в}/{H}{ρ_в}=800$ ${кг}/{м^3}$
Задача 2
Бутылка высотой 20 см с площадью 10 см2 заполнена водой. Чему равна сила давления воды на дно бутылки? Ускорение свободного падения принять равным 10 м/с2. Ответ представить в Н.
Решение
Давление $p=ρgh=1000·10·0.2=2000Па$
Сила давления $F=pS=2000·0,001=2$ Н
2 способ:
сила давления - есть вес жидкости
$F=P = mg=ρVg=ρShg=1000·0,001·0,2·10=2$ Н
Задача 3
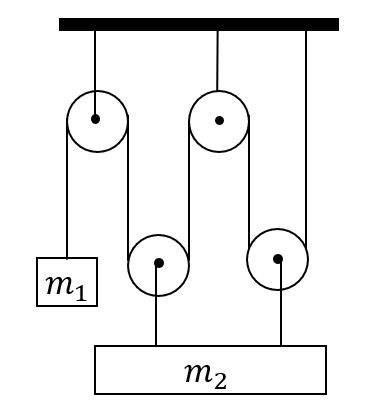
В системе, изображенной на рисунке, нити и блоки невесомы, трения нет. Каково должно быть отношение $m_2/m_1$, чтобы система находилась в равновесии?
Решение
С учётом свойств подвижных и неподвижных блоков получим силы натяжения нитей, действующие на грузы:
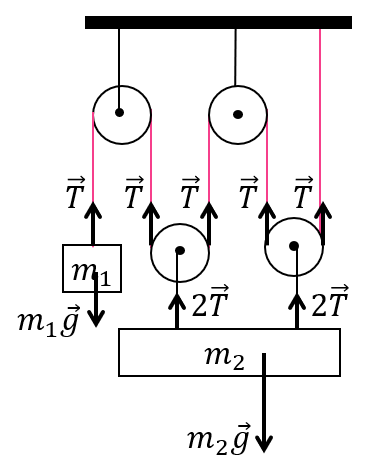
Условие равновесия для груза 1: $m_1g=T$
Условие равновесия для груза 2: $m_2g=2T+2T=4T$
$m_2/m_1={4T}/T=4$
Задача 4
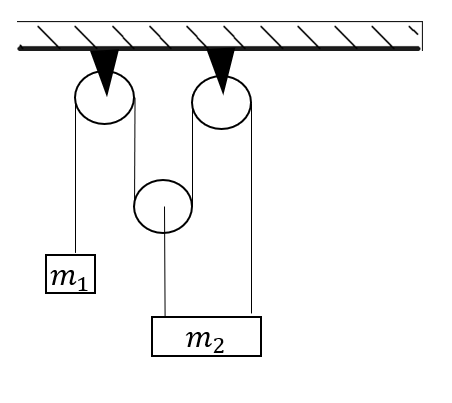
В системе, иображенной на рисунке, нити и блоки невесомы, трения нет. Каково должно быть отношение $m_2/m_1$, чтобы система находилась в равновесии?
Решение
С учётом свойств подвижных и неподвижных блоков получим силы натяжения нитей, действующие на грузы:
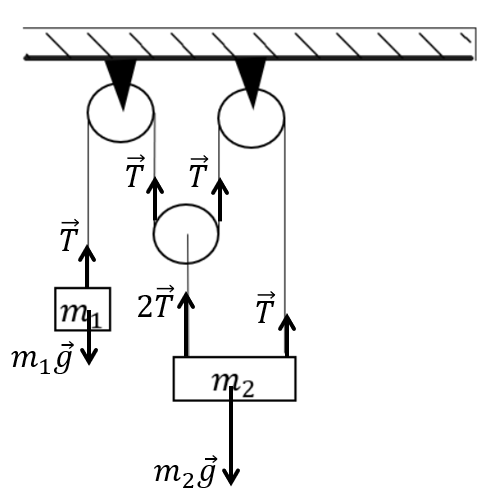
Условие равновесия для груза 1: $m_1g=T$
Условие равновесия для груза 2: $m_2g=2T+T=3T$
$m_2/m_1={3T}/T=3$
Задача 5
Чтобы удержать в равновесии груз, массой 10 кг , прикрепленный к левому концу рычага, необходимо приложить к правому концу силу 200 Н. Длина левого плеча 20 см. Чему равна длина рычага в (см) ?
Решение
Запишем уравнение моментов: OA*m*g=OB*F. От куда OB= 10 см. Тогда длинна рычага OA+OB = 30 см
Задача 6
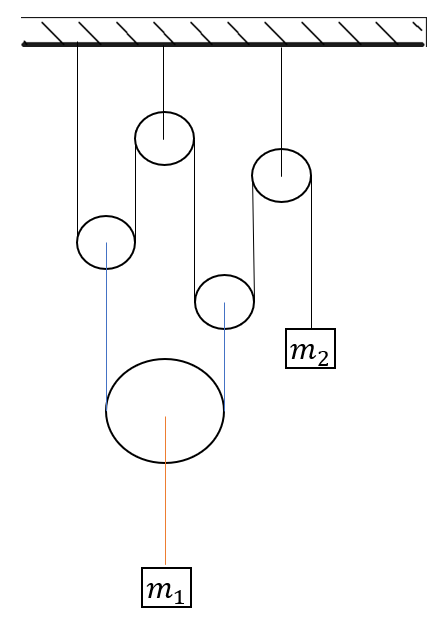
В системе, иображенной на рисунке, нити и блоки невесомы, трения нет. Каково должно быть отношение $m_2/m_1$, чтобы система находилась в равновесии?
Решение
Распишем проекции второго закона Ньютона:
$T_2=2T_1$
$
T_3=2T_2=4T_1$
$
T_1=m_{2}g$
$
T_3=m_{1}g$
$
4m_{2}g=m_{1}g$
$
m_2/m_1=0.25$
Задача 7
Женщина несет груз на легком коромысле . Чтобы удержать в равновесии груз, массой 5 кг , прикрепленный к левому концу коромысла А, она прикладывает ко второму концу B силу 40 Н. OB = 20 см. Чему равно OA? Ответ в см.
Решение
Запишем уравнение моментов $mg·OA= F·OB$. Подставим значения: $5·10·OA= 40·0.2$. От куда ОА=0,16 м = 16 см
Задача 8
Для измерения массы однородного стержня ученик воспользовался динамометром. Ученик положил стержень на стол и немного приподнял стержень за один из концов, при этом динамометр показал 10 Н. Чему равна масса стержня? Ответ выразите в кг.
Решение
Ось вращения расположим в том конце стержня, который опирается на стол. Запишем условие равновесия стержня через моменты относительно выбранной точки. Так как стержень однородный, сила тяжести приложена к его центру, тогда плечо силы тяжести будет $l/2$. Условие равновесия: mg0,5l-Fl=0. момент силы F, действующей на стержень со стороны динамометра, записываем со знаком минус, так как она вращает стержень против часовой стрелки? Подставив в условие равновесия значение силы F, получаем m=2 кг
Задача 9
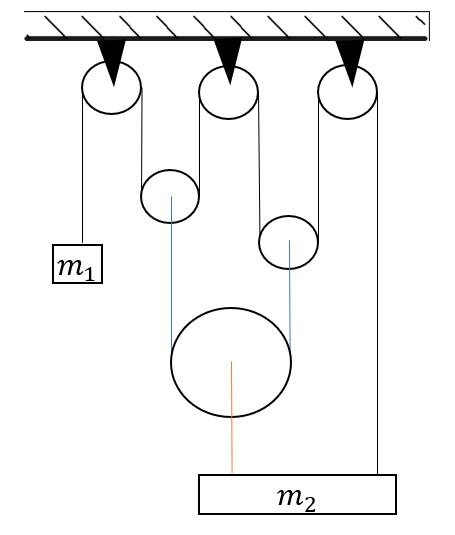
В системе, иображенной на рисунке, нити и блоки невесомы, трения нет. Каково должно быть отношение $m_2/m_1$, чтобы система находилась в равновесии?
Решение
Запишем проекции первого закона Ньютона:
$
T_1=m_1g$
$
2T_1=T_2$
$
2T_2=T_3$, то есть $T_3=4T_1$
$
T_3+T_1=m_{2}g$
$
5T_1=m_{2}g$
$
5m_1g=m_{2}g$
$
m_2/m_1=5$
Задача 10
Высота столба ртути ртутного барометра составляет 756 мм. Какова плотность жидкости жидкостного барометра, высота столба которого при данном атмосферном давлении равна 12 852 мм? Плотность ртути 13600 кг/м^3. Ответ выразите в (кг/м3).
Решение
Дано:
$h_p=756мм$
$p_p=13600{кг}/{м^3}$
$h_ж=12852мм$
$p_ж-?$
Решение:
Давление столба ртути равно давлению столба жидкости: $p_p=p_ж$(1), где $p_p=p_p·g·h_p$(2), $p_ж=p_ж·g·h_ж$(3), где $p_p$ и $p_ж$ - плотность ртути и жидкости жидкостного барометра.
Подставим (2) и (3) в (1) и найдем $p_ж$: $p_p·g·h_p=p_ж·g·h_ж⇒p_p·h_p=p_ж·h_ж$.
Подставим числовые значения в (4): $p_ж={13600·756}/{12852}=800{кг}/{м^3}$
Задача 11
Груз подвешен на лёгкой вертикальной пружине и совершает на ней колебания с циклической частотой ω = 10 рад/с, двигаясь по вертикали. Насколько растянется эта пружина, если аккуратно подвесить к ней тот же груз, не возбуждая колебаний? Ответ выразите в (см).
Решение
Дано:
$ω=10раз/с$
$g=10м/с^2$
$L-?$
Решение:
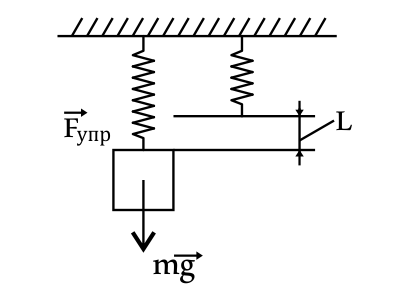
Жесткость пружины можно выразить как $k={mg}/{L}$(1), где $L$ - удлинение пружины под действием груза. Циклическая частота колебаний выражается как: $ω=√{{k}/{m}}=√{{g}/{L}}$(2). Тогда имеем: $ω^2={g}/{L}$, откуда $L={g}/{ω^2}={10}/{100}=0.1м=10см$
Задача 12
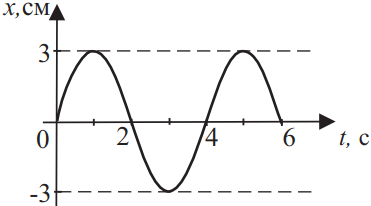
На рисунке представлена зависимость смещения пружинного маятника массой 200 г от времени. Какова потенциальная энергия в момент времени 1,5 с? В расчётах принять π2 ≈ 10. Ответ выразите в (мкДж).
Решение
Дано:
$m=0.2кг$
$t=1.5с$
$π^2=10$
$E_п-?$
Решение:
Потенциальная энергия равна: $E_п={kx^2}/{2}$(1), где $k$ - жесткость пружины, $x=x_m·sinωt=x_m·sin{2π}/{T}·t$(2), где $T$ - период колебаний пружинного маятника (из графика видно, что $T=4c$); $x_m=0.03м$ - амплитудное значение х.
Период колебаний пружинного маятника рассчитывается по формуле: $T=2π√{{m}/{R}}$(3), откуда найдем $k$: $T^2={4π^2m}/{k}⇒k={4π^2m}/{T^2}$(4)
Подставим числовые значения в (2) и в (4): $x=x_m·sin{2π}/{T}·t=0.03·sin{2π·1.5}/{4}=0.03·sin{3π}/{4}={0.03·√2}/{2}$. $k={4π^2m}/{T^2}={4·10·0.2}/{16}=0.5{Н}/{м}$.
Подставим числовые значения в (1): $E_п={kx^2}/{2}={0.5·(0.03·{√2}/{2})^2}/{2}={{0.0009·2·0.5}/{4}}/{2}={0.0009}/{8}=112.5·10^{-6}=112.5$мкДж.
Задача 13
Тело массой 40 г взвешивают на весах с разными плечами. Когда оно находится на левой чашке весов, его можно уравновесить грузом массой 20 г. Грузом какой массы можно уравновесить тело, если его положить на правую чашку весов? Ответ выразите в (г).
Решение
Дано:
$m_0=4·10^{-2}$кг
$m_1=2·10^{-2}$кг
$m_2-?$
Решение:
Составим уравнение на первое и второе взвешивание$\{\table\m_0·l_1=m_1·l_2; \m_0·l_2=m_2·l_1;$
Разделим первое уравнение на второе: ${m_0}/{m_2}={m_1}/{m_0}⇒m_2={m_0^2}/{m_1}={16·10^{-4}}/{2·10^{-2}}=80$г
Задача 14
Медный цилиндр массой 3,56 кг полностью опущен в бензин. Определите действующую на него архимедову силу. Плотность меди равна 8900 кг/м3. Плотность бензина равна 700 кг/м3. Ответ выразить в (H).
Решение
Дано:
$m_м=3.56$кг
$ρ_м=8900кг/м^3$
$ρ_б=700кг/м^3$
$F_{арх}-?$
Решение:
На погруженное в жидкость тело, действует выталкивающая сила $F_{арх}=ρ_б·g·V_м=ρ_б·g·{m_м}/{ρ_м}$
$F_{арх}={700·10·3.56}/{8900}=2.8H$
Задача 15
Матрос, стоящий на верхней палубе корабля, определил, что расстояние между следующими друг за другом гребнями волн равно 8 м. Кроме того, он подсчитал, что за 60 с мимо него прошло 23 волновых гребня. Какова скорость распространения волн? Корабль находился на стоянке. Ответ выразите в (м/с) и округлите до десятых.
Решение
Дано:
$λ=8$м
$t=60$с
$N=23$
$υ-?$
Решение:
Расстояние между соседними гребнями называется длиной волны $λ:λ=υ·t$(1), где $υ$ - скорость волны; $T={t}/{N}$(2) - период.
Подставим (2) в (1) и найдем $υ$: $λ={υ·t}/{N}⇒υ={λN}/{t}={8·23}/{60}=3.066м/с$.
Задача 16
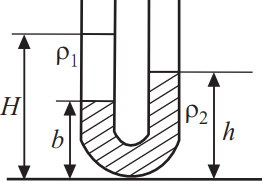
В широкую U -образную трубку с вертикальными прямыми коленами налиты подсолнечное масло и вода. На рисунке b = 12 см, h = 30 см, ρ1 — плотность подсолнечного масла, ρ2 — плотность воды. Найдите высоту столба жидкости H в левом колене. Ответ выразить в (см). Плотность воды 1000 кг/м^3. Плотность масла взять 900 кг/м^3.
Решение
Дано:
$b=12$см
$h=30$см
$ρ_1=ρ_м$
$ρ_2=ρ_в$
$H-?$
Решение:
$P_{лев}=Р_{прав}$, $ρ_1g(Н-в)=ρ_2g(h-в)$
$H={ρ_2(h-в)}/{ρ_1}+в={1000(18)}/{900}+12=32$см.
Задача 17
Определите подъёмную силу аэростата, вмещающего 5000 м3 гелия, если масса оболочки и гондолы со всеми приспособлениями равна 1000 кг. ρгелий = 0,18 кг/м3, ρвоздух = 1,29 кг/м3. Ответ выразите в (кН) с точностью до десятых.
Решение
Дано:
$V=5·10^3м^3$
$m_{груза}=10^3$кг
$g=10м/с^2$
$ρ_{гелий}=0.18{кг}/{м^3}$
$ρ_{воздух}=1.29{кг}/{м^3}$
$F-?$
Решение:
Подъемная сила воздушного шара равна разности между выталкивающей силы, направленной вверх и силой тяжести, направленной вниз: $F=F_{выт}-mg$(1), где $m=m_{гелия}+m_{груза}$(2). Масса гелия $m_{гелия}=ρ_{гелий}·V$(3), тогда выражение (2) примет вид: $m=ρ_{гелий}·V+m_{груза}$(4). Выталкивающая сила: $F_{выт}=ρ_{воздух}·g·V$(5).
Тогда подъемная сила: $F=ρ_{воздух}·g·V-(ρ_{гелий}·V+m_{груза})·g=1.29·10·5·10^3-(0.18·5000+1000)·10=64500-19000=45500=45.5$кН.
Задача 18
Вес груза в воздухе равен 2 Н. При опускании груза в воду на него действует сила Архимеда, равная 0,5 Н. Каков вес груза в воде? Ответ выразите в (H).
Решение
Дано:
$P_{возд}=2H$
$F_{арх}=0.5H$
$P_{вода}-?$
Решение:
По закону Архимеда вычислим: $P_{вода}=P_{возд}-F_{арх}=2-0.5=1.5H$.
Задача 19
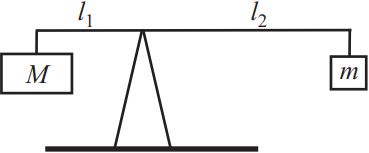
Тело массой 300 г взвешивают на весах с длинами плеч l1 и l2 соответственно, размещая его на правой чаше. Гирей какой массы можно его уравновесить, если длины плеч l1 и l2 относятся как 1 : 3? Ответ выразить в (г).
Решение
Дано:
$m=0.3$кг
${l_1}/{l_2}={1}/{3}$
$M-?$
Решение:
Составим уравнение баланса для системы.
$m·g·l_2=M·g·l_1$ - выразим М и получим.
$M={mgl_2}/{gl_1}={0.3}*{3}=900$г.
Задача 20
Какова глубина моря, если эхолокатор зафиксировал отражённый звук от дна моря через 1 с? Скорость звука в воде 1480 м/с. Ответ выразите в (м).
Решение
Дано:
$t=1$с
$υ_в=1480$м/с
$h-?$
Решение:
При эхолокации звук проходит путь $S$ равный $2h$, где $h$ - глубина моря, поскольку он проходит толщу воды, отражается от дна и идет обратно, т.е. $υ_в={S}/{t}={2h}/{t}$, откуда $2h=υ_в·t⇒h={υ_в·t}/{2}$.
Подставим числа: $h={1480·1}/{2}=740м$.
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ







