Задание 5. Механика. Анализ физических процессов. ЕГЭ 2026 по физике
Средний процент выполнения: 66.2%
Ответом к заданию 5 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Алгоритм решения задания 5:
- Определи, к какому разделу механики относится рассматриваемый физический процесс или явление.
- Выдели физическую модель, описывающую процесс: движение материальной точки, взаимодействие тел, равновесие, колебания или волны.
- Определи физические величины и параметры, характеризующие данный процесс или явление.
- Соотнеси ситуацию с соответствующими законами или принципами механики, применимыми к выбранной модели.
- Проанализируй взаимосвязь физических величин на основе выбранных законов и закономерностей.
- Сделай вывод о характере процесса или явления, опираясь на физический смысл используемых законов.
- Проверь, что вывод согласуется с условиями задачи и не противоречит физическим законам.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
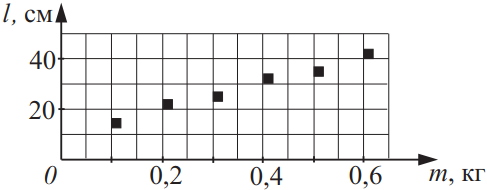
На рисунке приведён график зависимости длины пружины от величины нагрузки. Из приведённого ниже списка выберите два утверждения, соответствующих результатам этого эксперимента, и укажите их номера.
- Коэффициент упругости пружины примерно равен 20 Н/м.
- Коэффициент упругости пружины примерно равен 30 Н/м.
- Коэффициент упругости пружины примерно равен 50 Н/м.
- Коэффициент упругости пружины примерно равен 10 Н/м.
- Для данного эксперимента выполняется закон Гука.
Решение
$k=F/(l-l_0)$
Если продолжить прямую, видно, что длина недеформированной пружины 10 см
$k=2/(0.2-0.1)=20$ Н/м
Задача 2
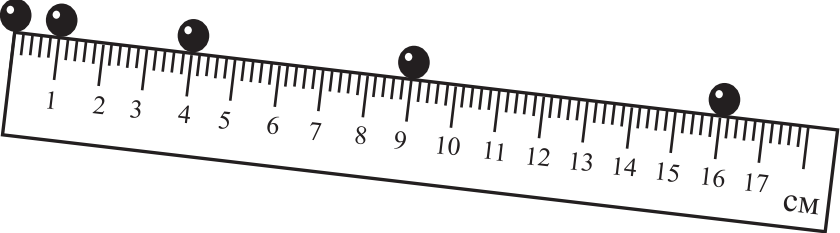
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.
- Движение шарика равномерное.
- Скорость шарика увеличивается.
- Шарик движется под действием переменной силы.
- Если промежуток времени между двумя последовательными положениями шарика равен 2 с, то его ускорение равно 0,5 см/с2.
- Импульс шарика в процессе движения остаётся постоянным.
Решение
1) Шарик за одинаковые промежутки времени проходит разные расстояния, значит, его движение неравномерное (не подходит).
2) Движение шарика равноускоренное, значит, скорость шарика увеличивается (подходит).
3) Шарик движется под действием постоянной силы $F↖{→}=ma↖{→}$ (не подходит).
4) $S=0.16м; t=4·2=8c; υ_0=0м/с; a=0.005м/с^2$. При равноускоренном движении перемещение равно: $S=υ_0е+{at^2}/{2}=0·8+{0.005·(8)^2}/{2}={0.005·64}/{2}=32·0.005=0.16=16$см (подходит).
Задача 3

Математический маятник совершает незатухающие колебания между точками А и Б. Точка О соответствует положению равновесия маятника. Используя текст и рисунок, выберите из предложенного ниже списка все верные утверждения. Укажите их номера.
- За время, равное периоду колебаний, маятник проходит путь, равный длине дуги АБ.
- При перемещении маятника из положения О в положение В потенциальная энергия уменьшается, а кинетическая энергия увеличивается.
- В точке О кинетическая энергия маятника максимальна.
- Расстояние АБ соответствует амплитуде колебаний координаты.
- В точках А и Б потенциальная энергия маятника принимает максимальное значение.
Решение
- За время, равное периоду колебаний, маятник проходит путь, равный ДВУМ длинам дуги АБ - "туда и обратно". 1 - неверно.
- При перемещении маятника из положения О в положение В потенциальная энергия УВЕЛИЧИВАЕТСЯ (т.к. высота растёт), а кинетическая энергия УМЕНЬШАЕТСЯ (т.к. маятник замедляется). 2 - неверно
- В точке О кинетическая энергия маятника максимальна, так как положение равновесия груз маятника проходит с наибольшей скоростью - верно
- Амплитуда колебаний координаты - это половина расстояния АБ - отклонение от положения равновесия. 4 - неверно.
- В точках А и Б потенциальная энергия маятника принимает максимальное значение, так как груз находится на наибольшей высоте. 5 - верно.
В точке О кинетическая энергия максимальна. Потенциальная энергия принимает максимальное значение в точках А и Б.
Задача 4
В таблице приведены результаты опытов по изучению движения без начальной скорости металлического шарика по гладкой наклонной плоскости. С помощью таблицы результатов измерений из приведённого ниже списка выберите два верных утверждения и укажите их номера.
| Время движения шарика, t, c | 0,4 | 0,5 | 0,6 | 0,8 |
| Перемещение шарика, S, см | 40 | 62,5 | 90 | 160 |
- Ускорение шарика равно 2 м/с2.
- Ускорение шарика равно 5 м/с2.
- Шарик движется равномерно.
- Угол наклона плоскости равен 30◦.
- Угол наклона плоскости равен 60◦.
Решение
1) Определим ускорение шарика $S=υ_0·t+{at^2}/{2}; 0.4=0+0.8a; a=5м/с^2$.
2) Определим угол (проекция $g↖{→}↓$).
$a=g·sinα; sinα=0.5; α=30°$
Задача 5
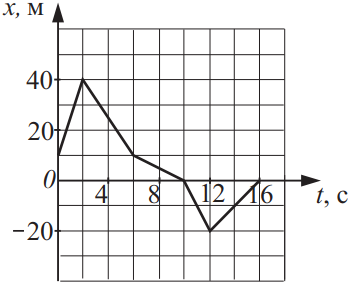
На рисунке приведена зависимость координаты движущегося тела от времени. Из приведённого ниже списка выберите два верных утверждения и укажите их номера.
- Ускорение движущегося тела менялось в процессе движения.
- Скорость тела в интервале времени от 2 до 6 с была в 3 раза больше, чем от 6 до 10 с.
- Максимальная скорость движения была равна 20 м/с.
- В момент времени 12 с тело изменило направление движения.
- Наименьшая скорость тела была в момент времени 12 с.
Решение
1) Ускорение движущегося тела не менялось в процессе движения, т.к. ветвей параболы на графике нет (не подходит).
2) Найдем скорость в интервале времени от 2 до 6с: $υ_{2-6}={x_6-x_2}/{6c-2c}={10-40}/{4}=-{30}/{4}=-7.5 м/с$. Найдем скорость в интервале времени от 6 до 10с: $υ_{6-10}={x_10-x_6}/{10c-6c}={0-10}/{4}=-{10}/{4}=-2.5м/с$. Тогда ${υ_{2-6}}/{υ_{6-10}}={-7.5}/{-2.5}=3$ (подходит).
3) Максимальная скорость движения была на интервале времени от 0 до 2с: $υ_{0-2}={x_2-x_0}/{2c-0c}={40-10}/{2}=15 м/с$ (не подходит).
4) В момент времени 12с тело изменило направление движения, т.к. $x(16c) > x(12c)$ (подходит).
Задача 6
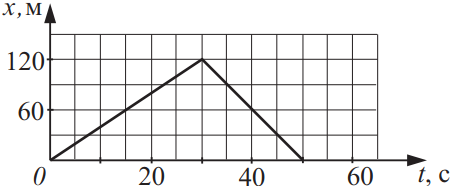
На рисунке приведена зависимость координаты движущегося тела от времени. Из приведённого ниже списка выберите два верных утверждения
- Скорость движения тела в интервале времени от 30 до 50 с на 2 м/с больше, чем скорость в интервале времени от 0 до 30 с.
- Скорость тела возрастала в интервале времени от 0 до 30 с и убывала в интервале от 30 до 50 с.
- Максимальная скорость движения на всём пути равна 2,4 м/с.
- За всё время движения тело прошло путь 120 м.
- За всё время движения тело прошло путь 240 м.
Решение
1) $υ_1[30-50c]={x_к-x_н}/{t_к-t_н}={0-120}/{50-30}=-{120}/{20}=-6 м/с$. Знак "минус" говорит о том, что тело движется в обратном направлении, поэтому возьмем по модулю $υ[30-50c]=6 м/с; υ_2[0-30c]={x_к-x_н}/{t_к-t_н}={120-0}/{30-0}={120}/{30}=4 м/с; ∆υ=υ_1[30-50c]-υ_2[0-30c]=6-4=2 м/с$(подходит).
2) Скорость тела возрастала в интервале времени от 0 до 30с и в интервале от 30 до 50с (не подходит).
3) Максимальная скорость на всем пути равна 6 м/с (не подходит).
4) За все время движения тело прошло путь: $S=S_1+S_2=υ_1·∆t_1+υ_1·∆t_2=6·(50-30)+4·(30-0)=6·20+4·30=120+120=240$м (не подходит).
5) За все время движения тело прошло путь 240м (подходит).
Задача 7
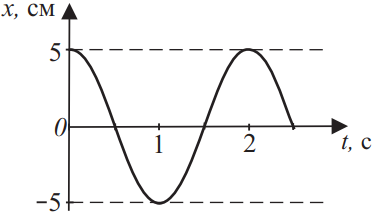
Координата колеблющегося тела меняется так, как показано на графике. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика. Укажите их номера.
- Тело совершает колебания с частотой 0,5 Гц.
- Координату тела в момент времени t можно найти по формуле x = 5 sin(π · t + π/2).
- Тело совершает колебания с частотой 5 Гц.
- Координату тела в момент времени t можно найти по формуле x = 5 sin(π/2 · t + π/2).
- Координату тела в момент времени t можно найти по формуле x = 5 cos(2π · t + π/2).
Решение
1) Из графика видно, что период колебаний тела $T=2$, тогда частота $v={1}/{T}={1}/{2}=0.5$Гц.
2) Уравнение колебаний в общем виде $x=x_m·sin(ω·t+ϕ_0)$. Из графика видно, что $x_m=5$см - амплитудное значение координаты и начальная фаза $ϕ_0={π}/{2}$, а циклическая частота $ω={2π}/{T}={2π}/{2}=π$Тогда: $x=5·sin(π·t+{π}/{2})$.
Задача 8
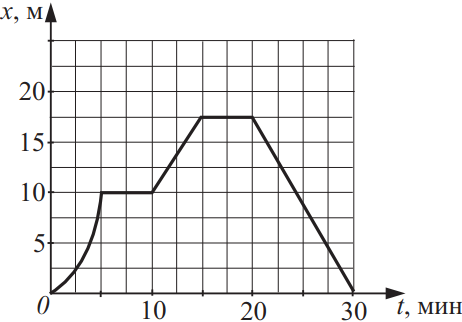
Материальная точка движется вдоль оси Ox. На рисунке представлен график зависимости координаты x этой точки от времени t. Из приведённого ниже списка утверждений выберите два правильных. Укажите их номера.
- Через полчаса тело вернулось в первоначальную точку.
- Первые пять минут тело двигалось равномерно.
- С 10-й по 15-ю минуты тело прошло 10 м.
- За первые полчаса движения было сделано 2 одинаковых по длительности остановки.
- С 20-й по 30-ю минуты тело двигалось со скоростью 1,5 м/мин.
Решение
По данному графику можно сказать, что через 30 минут тело вернулось в начальную точку. За первые 30 мин тело останавливалась с 5 по 10 и с 15 по 20 минуту на 5 минут.
Задача 9
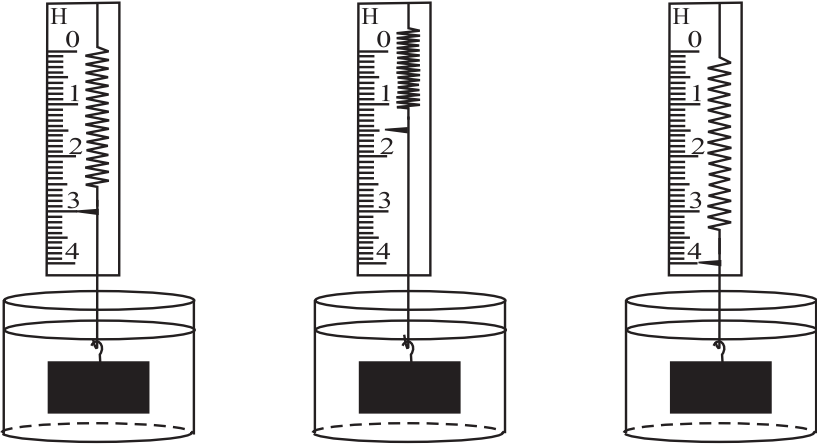
В сосуды с одинаковым объёмом воды (1000 ${кг}/{м^3}$), керосина (800 ${кг}/{м^3}$) и подсолнечного масла (920 ${кг}/{м^3}$) опускаются три одинаковых груза, вес которых в жидкости измеряется динамометром. Выберите из предложенного ниже списка два утверждения, соответствующих результатам опыта.
- Во втором сосуде находится вода.
- В первом сосуде (слева) находится керосин.
- Сила Архимеда зависит от массы груза.
- Наименьшей вес имеет груз, помещённый в третий сосуд.
- Вес груза в жидкости зависит от её плотности.
Решение
Так как плотность воды больше масла и керосина, сила Архимеда будет наибольшей, а вес тела наименьшим.
Задача 10
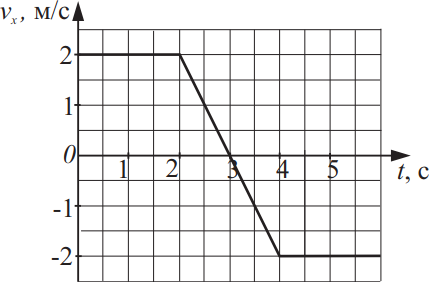
Тело массой 30 кг движется вдоль оси Ox в инерциальной системе отсчёта. График зависимости проекции скорости vx этого тела на ось Ox от времени представлен на рисунке. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика:
- В течение первых двух секунд и последних двух секунд тело двигалось равномерно.
- Модуль ускорения тела в промежутке времени от 2-й до 3-й секунд больше модуля ускорения тела в промежутке времени от 3-й до 4-й секунд.
- В промежутке времени от 2,5 до 3,5 секунд перемещение тела равно 50 см.
- В промежутке времени от 3,5 до 4-й секунд импульс тела уменьшился на 30 кг·м/с.
- В промежутке времени от 2 до 2,5 секунд кинетическая энергия тела уменьшилась в 4 раза.
Решение
Из анализа графика очевидно, что в течение первых 2-х секунд, тело двигалось равномерно $υ=const$, а в промежутке от 2 до 2.5 секунд, кинетическая энергия уменьшалась в 4 раза, а скорость уменьшалась в 2 раза.
Задача 11
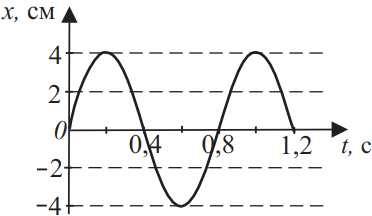
Координата колеблющегося тела меняется так, как показано на графике рисунка. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Период колебаний тела равен 1 с.
- Амплитуда колебаний равна 8 см.
- Частота колебаний равна 1,25 Гц.
- Амплитуда колебаний равна 4 см.
- Период колебаний тела равен 0,4 с.
Решение
Из данного графика очевидно, что $A=4$см (2 - неверно, 4 - верно), период колебаний T=0.8 c (1, 5 - неверно), а частота $v={1}/{T}={1}/{0.8}=1.25$Гц.(3 - верно)
Задача 12
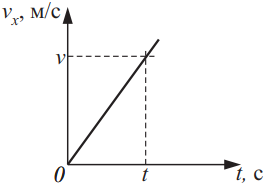
На рисунке изображён график зависимости проекции скорости тела массой m от времени (t). На основании графика выберите два верных утверждения из приведённого ниже списка для момента времени t. Укажите их номера.
- Движущаяся сила вычисляется по формуле F = m · v · t.
- Работу силы можно найти по формуле $A = {m· v}/{2t}$.
- Движущаяся сила вычисляется по формуле $F = {mv}/{t}$.
- Работу силы можно найти по формуле $A = {m·v^2}/{2}$.
- Работу силы можно найти по формуле $A = {m·v^2}/{2t^2}$.
Решение
3) Движущаяся сила $F=ma$, где $a={υ-υ_0}/{y}={υ}/{t}$, поскольку $υ_0=0$, что видно графика. Тогда $F=ma={mυ}/{t}$.
4) Работа силы равна изменению кинетической энергии, т.е. $A=∆E_к={mυ^2}/{2}-{mυ_0^2}/{2}$, поскольку $υ_0=0$, то $A={mυ^2}/{2}-0={mυ^2}/{2}$.
Задача 13
Грузик, подвешенный на нити, совершает гармонические колебания. В таблице представлены значения координаты грузика через одинаковые промежутки времени. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.
| t, c | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| x, см | 6 | 3 | 0 | 3 | 6 | 3 | 0 | 3 |
- Максимальная скорость грузика равна 0,15 м/с.
- Период колебаний шарика равен 0,4 с.
- В момент времени 0,1 с кинетическая энергия шарика максимальна.
- Полная механическая энергия шарика остаётся неизменной.
- Амплитуда колебаний шарика равна 6 мм.
Решение
Исходя из теории о гармонических колебаниях и данной таблицы, полная механическая энергия шарика остается неизменной. (4 - верно).
Период колебании - время за которое происходит одно полное колебание - 0,4 с (2 - верно)
Максимальная скорость шарика связана с амплитудой ( $υ_{max}=А ω ={А2π}/{T}= {0,03* 2*3.14}/{0,4}=0,471$м/с. (1 - неверно)
Максимальная кинетическая энергия будет в момент прохождения шариком положения равновесия x=3 см, это соответствует времени t=0,1 с (3 - верно)
Амплитуда колебания - это максимальное отклонение от положения равновесия, так как координата колеблется между значениями 6 см и 0, положению равновесия будет соответствовать координата х=3 см, значит амплитуда: А=6-3=3 см (5 - неверно)
Задача 14
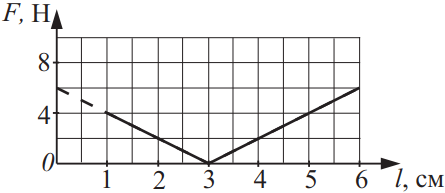
При проведении эксперимента ученик исследовал зависимость модуля силы упругости пружины, которая выражается формулой F (l) = k|l − l0|, где l0 — длина пружины в недеформированном состоянии, от её длины. График полученной зависимости приведён на рисунке. Из приведённого ниже списка выберите все верные утверждения на основании анализа графика и укажите их номера.
- Длина пружины в недеформированном состоянии равна 6 см.
- Длина пружины в недеформированном состоянии равна 3 см.
- При действии силы 2 Н деформация пружины равна 2 см.
- При действии силы 4 Н деформация пружины равна 2 см.
- Коэффициент жёсткости пружины равен 50 Н/м.
Решение
1) Из графика видно, что длина пружины в не деформированном состоянии равна 3 см, т.к. при l=3см сила упругости $F=OH$(не подходит).
2) Длина пружины в не деформированном состоянии равна 3 см (подходит).
3) При действии сила 2Н деформация пружины равна |2см-3см|=|-1см|=1см или |4см-3см|=1см (не подходит).
4) При действии сила 4Н пружина сжимается или растягивается на 2см, поскольку |1см-3см|=|-2см|=1см или |5см-3см|=2см (подходит).
5) Коэффициент жесткости $k={F}/{|l − l0|}={4 H}/{|5см-3см|}=200 {H}/{м}$ (не подходит)
Задача 15
Ученик исследовал зависимость модуля силы упругости F пружины от её растяжения x. Результаты эксперимента приведены в таблице. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
| F, H | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| x, м | 0 | 0,02 | 0,04 | 0,06 | 0,08 | 0,10 |
- Коэффициент упругости пружины равен 2,5 Н/м.
- При увеличении массы груза растяжение пружины уменьшается.
- Потенциальная энергия пружины пропорциональна растяжению пружины.
- Потенциальная энергия пружины при её растяжении на 0,08 м равна 0,08 Дж.
- При подвешенном к пружине грузе массой 100 г её удлинение составит 4 см.
Решение
Исходя из теории упругости и результатов опыта, определим $E_n={kx^2}/{2}={25·0.08^2}/{2}=0.08$Дж. $k={E}/{x}={2}/{0.08}=25$н/м, а при $F_т=1H; x=0.04$м.
Задача 16
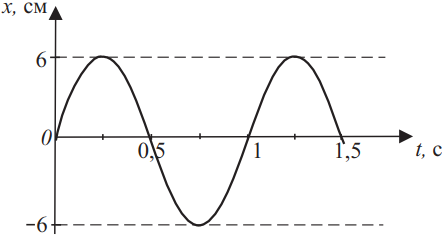
По экспериментальным данным построен график зависимости координаты колебания от времени на рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 6 см.
- Координату тела в момент времени t можно найти по формуле x = 6 sin(π · t).
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 0 см.
- Координату тела в момент времени t можно найти по формуле x = 6 cos(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 6 sin(2π · t).
Решение
1) Из графика видно, что период колебаний тела $T=1с$, амплитудное значение координаты $x_m=6$см. Значит, угловая частота тела $ω={2π}/{T}={2π}/{1}=2π$. Запишем уравнение колебаний в общем виде: $x=x_m·sin({2π}/{T}·t)$. Подставим наши данные, имеем: $x=6·sin({2πt}/{1})=6·sin(2π·t)$. Координата колебания подчиняется закону синуса, следовательно, в момент времени, равный 10 периодам колебаний, тело находится в точке с координатой $х=0$ см.
Задача 17
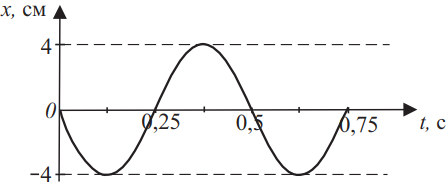
Координата колеблющегося тела меняется так, как показано на графике. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленного графика и укажите их номера.
- Тело совершает колебания с угловой частотой 2π.
- Координату тела в момент времени t можно найти по формуле x = 4 sin(4π · t + π).
- Тело совершает колебания с угловой частотой 4π.
- Координату тела в момент времени t можно найти по формуле x = 4 sin(2π · t + π).
- Координату тела в момент времени t можно найти по формуле x = 4 cos(π · t + π).
Решение
1) Из графика видно, что период колебаний тела $T=0.5с$, амплитудное значение координаты $x_m=4$см. Значит, угловая частота тела $ω={2π}/{T}={2π}/{0.5}=4π$. Запишем уравнение колебаний в общем виде: $x=x_m·sin(ωt+ϕ_0)$. В нашем случае колебания происходят по закону синуса, т.к. мы видим график синусоиды, проходящей через начало координат точку с координатами (0;0) и начальной фазой $ϕ_0=π$. Запишем уравнение: $x=4·sin(4πt+π)$.
Задача 18
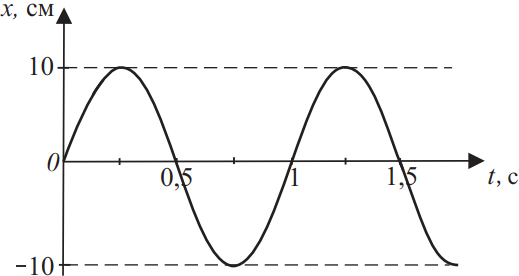
Координата колеблющегося тела меняется так, как показано на графике рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- Период колебаний тела равен 1 с.
- Координату тела в момент времени t можно найти по формуле x = 0,1 sin(π · t + π/4).
- Тело совершает колебания с периодом 0,1 с.
- Координату тела в момент времени t можно найти по формуле x = 10 sin(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 10 cos(2π · t + π/4).
Решение
1) Из графика видно, что период колебаний тела равен 1с.
4) Поскольку координата колеблющегося тела изменяется по закону синуса, $x_m=10$см - амплитудное значение координаты и начальная фаза $ϕ_0=0$, то координату тела в момент времени $t$ можно найти по формуле $x=10·sin(2π·t)$.
Задача 19
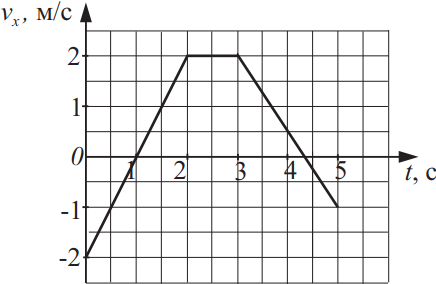
Тело массой 15 кг движется вдоль оси Ox в инерциальной системе отсчёта. График зависимости проекции скорости vx этого тела на ось Ox от времени представлен на рисунке. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленного графика и укажите их номера.
- В течение первых двух секунд перемещение тела равно 2 м.
- Модуль ускорения тела в промежутке времени от 1 с до 2 с на 25% больше модуля ускорения тела в промежутке времени от 3 с до 4 с.
- В течение первой секунды кинетическая энергия тела увеличилась на 30 Дж.
- В промежутке времени от 1 с до 2 с импульс тела увеличился в 2 раза.
- В момент времени 4 с модуль равнодействующей сил, действующих на тело, равен 22,5 Н.
Решение
Из теории кинематики и данного графика можно сказать, что модуль ускорения тела с 1 до 2 на 25% больше 3-4, т.е. $a_{1-2}=2м/с^2; a_{3-4}=1.5м/с^2$. В момент времени 4с модуль равнодействующих сил, $F=22.5H$, т.к. $a_4=1.5м/с^2$, $F_p=ma_4=15·1.5=22.5H$
Задача 20
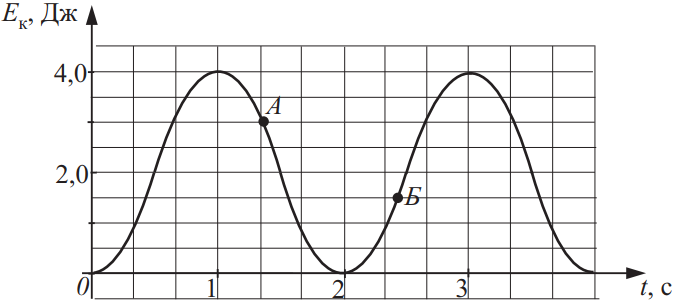
На рисунке приведён график зависимости кинетической энергии тела от времени t. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Тело совершает гармонические колебания.
- Потенциальная энергия тела в точке A равна 1 Дж.
- Период колебаний тела равен 2 с.
- Максимальное значение потенциальной энергии равно потенциальной энергии в точке Б.
- Частота колебаний тела равна 4 Гц.
Решение
1. Тело совершает гармонические колебания, т.к. гармонические колебания - это колебания, подчиняющиеся закону синуса или косинуса, а на графике мы видим синусоиду (1 - верно).
2. Поскольку полная механическая энергия тела равна: $E=E_{п,max}=E_{п,max}=E_к+Е_п$(1), где $E_к$ - кинетическая энергия тела, $E_{к,max}=4$Дж, $E_п$ - потенциальная энергия тела. В точке А $E_к=3$Дж, значит, $E_п=E-E_к=E_{к,max}-E_к=4-3=1$Дж (2 - верно)
3. За один период колебаний тела, успевает произойти два колебания кинетической энергии, поэтому период колебаний тела равен 4с, а не 2. (3 - неверно)
4. Максимальное значение потенциальной энергии будет в той точке, в которой кинетическая энергия минимальна. Точка Б под это условие не подходит (4 - неверно)
5. Частота колебания тела равна: $v=1/T=1/4=0,25$ Гц (5 - неверно)
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ







