Задание 6. Механика. Изменение физических величин. ЕГЭ 2026 по физике
Средний процент выполнения: 69.2%
Ответом к заданию 6 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Алгоритм решения задания 6:
- Определи, какой физический процесс или явление описано, и к какому разделу механики оно относится.
- Выбери физическую модель, соответствующую описываемому процессу или явлению.
- Выдели физические величины, характеризующие процесс, и установи их взаимосвязи.
- Соотнеси ситуацию с основными законами или принципами механики, применимыми к данной модели.
- Используй выбранные физические величины и законы для анализа процесса или явления.
- Сформулируй вывод, опираясь на физический смысл используемых законов и величин.
- Проверь, что вывод согласуется с условиями задания и не противоречит изученным законам физики.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Грузик колеблется на пружинке, при чем пружинка всегда остается в растянутом состоянии. Что будет происходить с потенциальной энергией груза и растяжением пружины при движении из положения равновесия вниз?
К каждой величине подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
В ответе запишите только цифры без пробелов и запятых в следующем порядке: характер изменения потенциальной энергии груза, характер изменения растяжения пружина
Решение
Потенциальная энергия грузика будет уменьшаться, поскольку он будет ближе к земле. Растяжение же пружины напротив будет увеличиваться.
Задача 2
Грузик колеблется на пружинке, при чем пружинка всегда остается в растянутом состоянии. Что будет происходить со скоростью груза и потенциальной энергией пружины при движении из положения равновесия вверх? (Цифры в ответе могут повторяться)
1) увеличится 2) уменьшится3) не изменится
Решение
По скольку пружина в любом случае растянута, значит потенциальная энергия пружины будет уменьшаться, так как растяжение будет становится меньше. Но и кинетическая энергия тоже будет становиться меньше, так как по мере приближения к верхней точке колебания скорость груза уменшается.
Задача 3
Каучуковый мяч, летящий горизонтально, упруго ударяется о вертикальную стену. Установите соответствие между физическими величинами, описывающими удар, и формулами для их нахождения.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические явления | Формулы |
| А) изменение импульса Б) средняя сила удара | 1) mv 2) 2mv 3) ${mv}/{t}$ 4) ${2mv}/{t}$ |
Решение
А) Изменение импульса $∆p=mυ-(-mυ)=2mυ$, т.к. скорость (пар) изменили направление на противоположное и удар упругий.
Б) Средняя сила удара $F_{ср}={∆p}/{t}⇒{2mυ}/{t}$ воспользуемся формулами из основ кинематики.
Задача 4
Телу массой m, находящемуся на вершине наклонной плоскости высотой h и длиной l, сообщают начальную скорость v0. В самом низу наклонной плоскости тело останавливается. Коэффициент трения тела о плоскость равен µ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические величины | Формулы |
| А) работа силы трения Б) модуль силы трения | 1) $mgh + {mv_0^2}/{2}$ 2) $−µmgl$ 3) $−mgh −{mv_0^2}/{2}$ 4) ${µmg√{l^2 − h^2}}/{l}$ |
Решение
Дано:
$m, h, l, υ_0$
$μ, g$
$F_{тр}-?|F_{тр}|-?$
Решение:
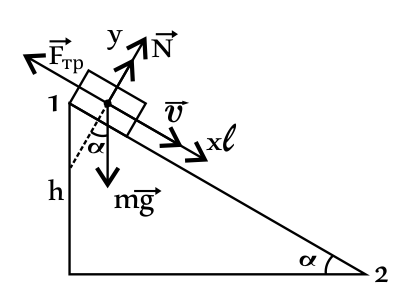
Работа силы трения равна: $A=∆E$(1), где $∆E=E_2-E_1$(2).
Полная механическая энергия в (1) равна: $E_1=mgh+{mυ_0^2}/{2}(3), E=0$(4).
Тогда имеем: $A=∆E=E_2-E_1=0-mgh-{mυ_0^2}/{2}=-mgh-{mυ_0^2}/{2}$.
Модуль силы трения равен: $|F_{тр}|=μN=μmg·cosα$, где $cosα={√{l^2-h^2}}/{l}$, тогда имеем: $|F_{тр}|={μmg√{l^2-h^2}}/{l}$
Задача 5
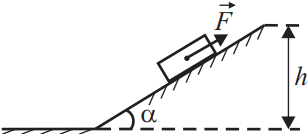
Тело массой m удерживается в покое на шероховатой наклонной опоре с углом α к горизонту с помощью силы F. Коэффициент трения тела о плоскость равен µ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические величины | Формулы |
| А) модуль силы F Б) модуль силы трения | 1) mg sin α − µmg cos α 2) mg sin α + µmg cos α 3) µmg cos α 4) mg sin α |
Решение
Дано:
$m, α, F, μ$
$|F|-?|F_{тр}|-?$
Решение:
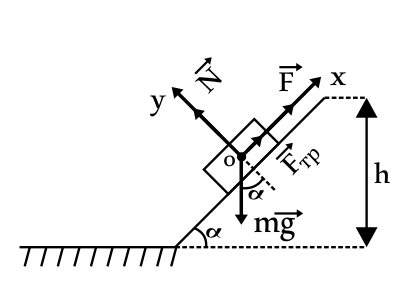
Запишем II закон Ньютона: $m{a}↖{→}=F↖{→}+N↖{→}+{F_{тр}}↖{→}+m{g}↖{→}$(1).
В проекциях на оси Ох и Оу: $Ox: O=F+F_{тр}-mgsinα$(2)
$Oy: O=N-mgcosα$(3)
Из уравнения (2) имеем: $F=mgsinα-F_{тр}$(4), учитывая, что $F_{тр}=μN$(5) и $N=mgcosα$(6), имеем: $F=mgsinα-F_{тр}=mgsinα-μmgcosα$(8).
Задача 6
В первой серии опытов по исследованию малых колебаний разных грузиков на нерастяжимой нити одинаковой длины использовался железный грузик, во второй — деревянный такого же объёма. Как при переходе от первой серии опытов ко второй изменятся частота колебаний и максимальная кинетическая энергия грузика, если максимальный угол отклонения нити от вертикали в обоих исследованиях был одинаковый? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Частота колебаний Б) Максимальная кинетическая энергия грузика | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Так как маятник математический $T=2π√{{l}/{g}}; T={1}/{v}$ частота не зависит от массы (не изменится). $E_к={mυ^2}/{2}$ (кинетическая энергия уменьшится, т.к. дерево легче, чем железо).
Задача 7
В верхних слоях атмосферы высота полёта искусственного спутника над Землёй уменьшилась с 500 до 200 км. Как изменились в результате этого его кинетическая энергия и период обращения? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Кинетическая энергия Б) Период обращения | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Дано:
$H_1=500$км
$H_2=200$км
$∆E_к-?$
$∆T-?$
Решение:
1) $∆E_к$. Из закона сохранения энергии очевидно, что при уменьшении потенциальной энергии увеличивается кинетическая.
2) Радиус орбиты уменьшается, скорость движения увеличивается, следовательно, период обращения спутника уменьшается $T={2πR}/{υ}$.
Задача 8
Мячик бросают вертикально вверх с высоты балкона третьего этажа, после он падает на землю. Что произойдёт с конечной скоростью мяча и его ускорением, если, не меняя начальной скорости, так же бросить его с балкона пятого этажа? Сопротивление воздуха не учитывать. Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Конечная скорость Б) Ускорение | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
1. Если мячик бросить с балкона пятого этажа, не меняя начальной скорости, то его конечная скорость увеличится, т.к. время падения с пятого этажа больше времени падения с третьего этажа: $υ_к=υ_0+gt_{пад}$(1), где $t_{пад}$ - время падения.
2. Ускорение мячика не изменится, т.к. свободное падение всех тел происходит с одинаковым ускорением - ускорением свободного падения $g↖{→}$.
Задача 9
Установите соответствие между физической величиной и её выражением через основные единицы СИ.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физическая величина | Её выражение в СИ |
| А) импульс Б) давление | 1) $кг · {м^2}/{с^2}$ 2) ${кг}/{м · с^2}$ 3) ${кг·м}/{с^2}$ 4) ${кг·м}/{с}$ |
Решение
А) Импульс $p↖{→}=mυ↖{→}[кг{м}/{с}]$.
Б) Давление $p={F}/{S}[{кг}/{м·с^2}]$.
Задача 10
К динамометру подцепили твёрдое тело. Как при этом изменились жёсткость пружины и её потенциальная энергия? Для каждой величины определите соответствующий характер изменения:
| Физической величины | Характер изменения |
| A) Жёсткость пружины Б) Потенциальная энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Потенциальная энергия пружины $E_п={kx^2}/{2}$, где $k$ - жесткость пружины, $x$ - удлинение пружины. Когда к динамометру подцепили твердое тело, то потенциальная энергия пружины увеличилась, т.к. увеличилось удлинение пружины. Жесткость же пружины осталась неизменной, т.к. не зависит от того висит или растягивает какое-либо тело пружину динамометра или нет.
Задача 11
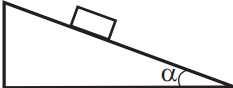
Тело массой m покоится на наклонной плоскости, расположенной под углом α к горизонту, µ — коэффициент трения. Установите соответствие между физическими величинами и формулами для их вычисления.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические величины | Формулы |
| А) сила трения покоя Б) сила реакции опоры | 1) 0 2) mg sin α 3) µmg sin α 4) mg cos α |
Решение
2 закон Ньютона в проекциях на ось x, направленную вдоль плоскости вниз, и на ось y, направленную перпендикулярно плоскости вверх:
Ox: $m·g·sinα-F_{тр}=0$, следовательно, $F_{тр}=m·g·sinα$ (сила трения покоя)
Oy: $N-m·g·cosα=0$, следовательно, $N=m·g·cosα$ (сила реакции опоры)
Задача 12
Ракета движется с постоянной скоростью.Сопло ракеты повернули так, что оно располагается перпендикулярно к скорости ракеты. Из сопла вылетают продукты сгорания топлива, в результате чего на ракету действует сила, направленная перпендикулярно скорости ракеты. Что произойдёт с модулем скорости ракеты и её кинетической энергией? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Модуль скорости ракеты Б) Кинетическая энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Дано:
$υ=const$
Решение:
1) Модуль скорости ракеты не изменится, т.к. сопло тоже, только другое положение.
2) Т.к. скорость не изменялась, то и кинетическая энергия не изменилась.
Задача 13
При вертикальном подъёме тела массой m на высоту h совершена работа A. С каким ускорением двигалось тело? Сколько по времени длился подъём тела? Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические величины | Формулы |
| А) ускорение тела a Б) время подъёма t | 1) $√{{2mh^2}/{A-mgh}}$ 2) ${A}/{h·m}-g$ 3) $√{2gH}$ 4) $A·h·m-g$ |
Решение
Дано:
$h, m, A$
$А)a-?;Б)t-?$
Решение:
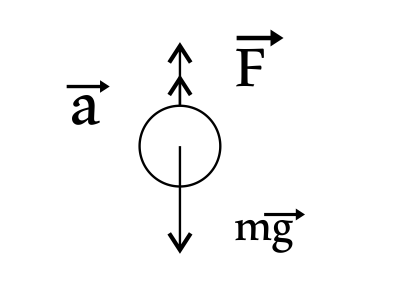
A) При подъеме тела на высоту $h$ с ускорением $a$ действует сила $F$. Запишем второй Ньютона: $ma=F–mg$, откуда $F=m(a+g)$, тогда $A=F·h=m(a+g)·h$, откуда ускорение $a={A}/{m·h}-g$.
Б) Выражение для времени подъема $t$ найдем, проанализируя единицы измерения в формулах: $√{{2mh^2}/{A-mgh}}=√{{кг·м^2}/{Дж}}=√{{кг·м^2}/{Н·м}}=√{{кг·м·с^2}/{кг·м}}=√{с^2}=с$..
Или выразим время из уравнения: $h={at^2}/2$, тогда $t=√{{2h}/{a}}=√{{2h}/{{A-mhg}/{mh}}}=√{{2mh^2}/{A-mgh}}$
Задача 14
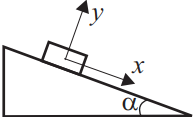
Тело массой m скатывается по наклонной плоскости, расположенной под углом α к горизонту, µ — коэффициент трения. Установите соответствие между физическими величинами и формулами для их вычисления.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические величины | Формулы |
| А) проекция ускорения тела на ось Ox Б) проекция силы реакции опоры на ось Oy | 1) g(sin α + µ cos α) 2) g(sin α − µ cos α) 3) µmg cos α 4) mg cos α |
Решение
Для движения тела по наклонной плоскости проекции ускорения тела на ось Ох $g(sinα-μcosα)$, из 2 закона Ньютона $ma=mgsinα-mμcosα$, проекция силы реакции опоры на ось Оу $mgcosα$.
Задача 15
Установите соответствие между физической величиной и её выражением через основные единицы СИ.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физическая величина | Её выражение в СИ |
| А) сила Б) работа | 1) ${м}/{с^2}$ 2) ${кг}/{м·с^2}$ 3) ${кг·м}/{с^2}$ 4) ${кг·м^2}/{с^2}$ |
Решение
А) Сила, знаем 2-й закон Ньютона $F∆t=∆p↖{→}$ выразим $F={∆p↖{→}}/{∆t}=[{кг·м}/{с^2}]$.
Б) Работа $A=F·S=[{кг·м^2}/{с^2}]$.
Задача 16
Тело движется по окружности с постоянной по модулю скоростью из верхней точки. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут описывать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Графики | Физические величины |
А) 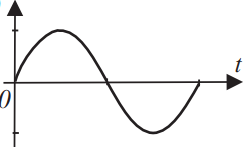 Б)  | 1) координата x 2) проекция скорости vx 3) кинетическая энергия Ek 4) проекция ускорения ax |
Решение
1) Соответствует координата Х, т.к. $υ=ω·R=const$. Тело будет иметь данный график.
2) $E_к$ будет постоянной, т.к. $E_к={mυ^2}/{2}; υ=const$.
Задача 17
Тело лежит на краю горизонтально расположенного диска, вращающегося вокруг оси с увеличивающейся угловой скоростью. Как меняются сила трения, действующая на тело, и линейная скорость тела? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Сила трения Б) Линейная скорость тела | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
1) Центробежную силу компенсирует сила трения $m·{υ^2}/{R}=F_{тр}$, при росте $ω⇒υ=ωR$ увеличивается и сила трения то же.(1)
2) Линейная скорость $υ=ωR$ прямопропорционально растет.(1)
Задача 18
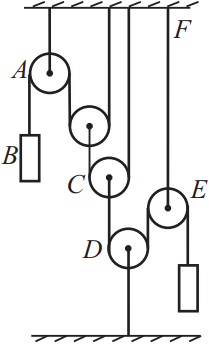
С помощью системы невесомых блоков на невесомых и нерастяжимых нитях уравновешены два груза. Модуль силы натяжения участка нити AB равен T/2. Установите соответствие между модулями сил натяжения и участками нитей. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Участки нитей | Модули сил натяжения |
| А) DC Б) EF | 1) T 2) 2T 3) 4T 4) 8T |
Решение
Будем отсчитывать блоки слева направо. На левой нити второго блока сила натяжения равна ${T}/{2}$, следовательно, чтобы блок оставался в равновесии, на центр блока действует сила $T$. Аналогично второму блоку на центр третьего блока действует сила $2T$, тогда сила натяжения, действующая на участок нити СD равна $2T$. Такая же сила натяжения будет на правой нити четвертого блока. Чтобы пятый блок находился в равновесии, необходимо, чтобы центр блока действовала сила $4T$.
Задача 19
Пружинный маятник совершает вертикальные колебания. Как изменятся частота колебаний и жёсткость пружины, если увеличить массу груза? Для каждой величины определите соответствующий характер изменения:
| Физической величины | Характер изменения |
| A) Частота колебаний Б) Жёсткость пружины | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Известно, что период колебаний пружинного маятника равен $T=2π√{{m}/{k}}$, где $m$ - масса груза, $k$ - жесткость пружины. Учитывая, что частота $v={1}/{T}$ или $v={1}/{2π}√{{k}/{m}}$, видно, что при увеличении массы груза, частота колебаний $v$ уменьшится. Масса груза на жесткость пружины не влияет, следовательно, жесткость пружины не изменится.
Задача 20
Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания.Пружина всё время растянута. Как ведёт себя кинетическая энергия груза и потенциальная энергия груза в поле силы тяжести, когда груз движется вверх от положения равновесия? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Кинетическая энергия груза Б) Потенциальная энергия груза в поле силы тяжести | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
При движении груза на пружине вверх кинетическая энергия груза уменьшается, т.к. скорость груза уменьшается, а потенциальная энергия в поле силы тяжести увеличивается.
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

