Задание 7. Тепловое равновесие, уравнение состояния. ЕГЭ 2026 по физике
Средний процент выполнения: 78.8%
Ответом к заданию 7 по физике может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 7:
- Определи, какой электрический процесс или элемент электрической цепи рассматривается в задании.
- Выдели физические величины, описывающие электрический ток, напряжение и сопротивление.
- Установи, какие из этих величин заданы, а какие требуется определить или проанализировать.
- Соотнеси описанную ситуацию с законом Ома для участка цепи.
- Запиши закон Ома в общем виде с использованием соответствующих физических величин.
- Примени записанный закон для анализа процесса или получения требуемого результата.
- Проверь, что результат согласуется с физическим смыслом электрических величин.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Во сколько раз увеличится давление идеального газа, если концентрацию увеличили в 4 раза, а температуру уменьшить в 2 раза ?
Решение
По основному уравнению МКТ: $p=nkT $ . Тогда во втором случае $ p_2 = 4nk {T}/{2}= 2nkT = 2p $ . То есть давление увеличится в 2 раза.
Задача 2
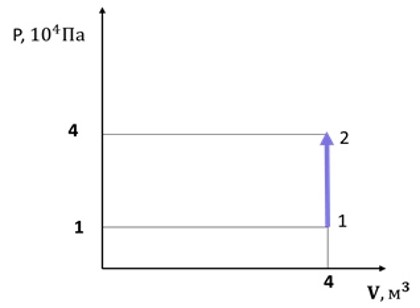
На рисунке изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 1 равна 127 °С. Какая температура соответствует состоянию 2? Ответ выразите в (К).
Решение
1) Не забываем осуществить перевод в Кельвины: $𝑇_1+127°С= 400К$
2) Записываем уравнение М-К для 1 и 2 точки: $𝑝_1𝑉=𝜈𝑅𝑇_1$ , $𝑝_2𝑉=𝜈𝑅𝑇_2$, тогда ${𝑝_1}/{p_2}={𝑇_1}/{T_2}$ , ${1}/{4}={𝑇_1}/{T_2}$ ${T_2= 4T_1=1600К}$
Задача 3
При температуре 400К и давлении p, 2 моль идеального газа занимают объём V. Какая температура 1 моля этого газа в объёме 4V при давлении p? Ответ в К.
Решение
1) Записываем уравнение Менделеева-Клапейрона для первого и второго случая: $pV=2RT_1$ (здесь мы сразу подставили число молей) $p4V=1RT_2$
2) Делим 1ое выражение на второе ${1}/{4}={2T_1}/{T_2}$ , откуда $T_2=8T_1$, то есть 3200 К
Задача 4
При температуре 80 K некоторое количество молекул газа азота N2 создаёт давление 300 Па. Азот нагрели до 3000 К, в результате чего все молекулы азота распались на атомы. Чему равно установившееся давление при температуре 3000 К? Ответ выразите в (кПа).
Решение
Дано:
$T_0=80K$
$P_0=300$Па
$T_2=3000K$
$P_2-?$
Решение:
1) $\{\table\P_0=n_0KT_0; \P_2=n_2KT_2;$ $n_2=2·N_0$, т.к. молекулы азота распались на атомы.
$P_2={2·P_0·T}/{T_0}={2·300·3000}/{80}=22.5$кПа.
Задача 5
В закрытом сосуде находится 120 г газа при комнатной температуре. Какая масса газа вытечет из сосуда, если после открытия крана давление в сосуде понизится в 4 раза? Ответ выразите в (кг).
Решение
Дано:
$T=20+273=293К$
$P_2={P_1}/{4}$
$m_1=0.12$кг
$∆m-?$
$T=const$
$V=const$
Решение:
Зная уравнение Менделеева-Клайперона составим систему 1 и 2.
$\{\table\P_1V={m}/{M}·RT_1; \P_2V={m}/{M}·RT_2;$, то $4={m_1}/{m_2}; m_2=0.03$.
$∆m=m_1-m_2=0.12-0.03=0.09$кг.
Задача 6
Определите температуру азота, имеющего массу 4 г, занимающего объём 831 см3 при давлении 0,2 МПа. Ответ выразите в (К). (Молярная масса азота $28·10^(-3)$кг/моль
Решение
Дано:
$T-?$
$m=4·10^{-3}кг$
$V=831см^3$
$p=0.2·10^6$
$T_?$
Решение:
По закону Менделеева-Клапейрона $pV={m}/{M}R·T; T={pV·M}/{m·R}$
$T={0.2·10^6·831·10^{-6}·0.028}/{4·10^{-3}·8.31}=140K$
Задача 7
Газ, занимающий объём 12,32 л, охладили при постоянном давлении на 45 К, после чего его объём стал равен 10,52 л. Какова была первоначальная температура газа? Ответ выразите в (К).
Решение
Дано:
$∆T=45K$
$V_1=12.32·10^{-3}м^3$
$V_2=10.52·10^{-3}м^3$
$p_1=p_2=p=const$
$T_1-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2V_2}/{T_2}$(1), учитывая, что $p=const$, имеем: ${pV_1}/{T_1}={pV_2}/{T_2}$ или $V_1T_2=V_2T_1$(2). Так как газ охладили, то $T_2=T_1-∆T$(3). Подставим (3) в (2): $V_1T_1-V_1∆T=V_2T_1⇒T_1={V_1∆T}/{(V_1-V_2)}={12.32·10^{-3}·45}/{1.8·10^{-3}}=308K$.
Задача 8
Концентрация молекул углекислого газа в сосуде составляет 3 · 1023м−3. Чему равна плотность газа? Ответ выразите в (г/м3). (Молярная масса углекислого газа $44·10^{-3}$ кг/моль, $N_A=6·10^{23}{1}/{моль}$)
Решение
Дано:
$n=3·10^{23}м^{-3}$
$μ(CO_2)=(12+16·2)·10^{-3}{кг}/{моль}=44·10^{-3}{кг}/{моль}$
$N_A=6·10^{23}{1}/{моль}$
$p-?$
Решение:
Концентрация молекул связана с плотностью соотношением: $n={p}/{m_0}$(1), откуда $p=n·m_0$(2), где $m_0$ - масса одной молекулы $CO_2$.
$m_0={μ}/{N_A}$(3), где $μ$ - молярная масса $CO_2$; $N_A$ - постоянная Авогадро.
Подставим (3) в (2): $p={n·μ}/{N_A}$(4). Подставим числовые значения: $p={3·10^{23}·44·10^{-3}}/{6·10^{23}}=22·10^{-3}{кг}/{м^3}=22г/м^3$
Задача 9
При повышении температуры идеального газа на 100 К среднеквадратичная скорость движения молекул выросла с 200 м/с до 600 м/с. Насколько надо понизить температуру газа, чтобы среднеквадратичная скорость уменьшилась с 600 м/с до 400 м/с? В ответе запишите на сколько (K).
Решение
Дано:
$∆T=100K↑$
$υ_{cр_1}=200$м/с
$υ_{cр_2}=600$м/с
$∆T'-?↓$
$υ_{cр_2}=600$м/с
$υ_{cр_3}=400$м/с
Решение:
Энергия: $E_к=3/2kT=3/2R/μT={mυ^2}/2$.
В первом процессе $T_1={υ_1^2μ}/{3R}$
$T_2={υ_2^2μ}/{3R}$
$∆T=T_2-T_1={μ}/{3R}·(υ_2^2-υ_1^2)$
${μ}/{3R}={∆T}/{υ_2^2-υ_1^2}={1}/{3200}$
Тогда $∆T'={μ}/{3R}(υ_3^2-υ_2^2)={1}/{3200}(400^2-600^2)=-62.5K$
$|∆T'|=62.5K$
Задача 10
Сосуд вместимостью 12 л, содержащий газ при давлении 0,4 МПа, соединяют с другим сосудом, из которого откачан воздух. Найдите конечное значение давления. Процесс изотермический (происходит при постоянной температуре). Вместимость второго сосуда равна 3,0 л. Ответ выразите в (МПа).
Решение
Дано:
$V_1=12·10^{-3}м^3$
$V_2=3·10^{-3}м^3$
$p_1=0.4·10^6$Па
$T_1=T_2=T=const$
$p_2-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2(V_2+V_1)}/{T_2}$(1), т.к. $T_1=T_2=T=const$, можно записать: $p_1V_1=p_2(V_2+V_1)$(2), откуда $p_2={p_1V_1}/{(V_2+V_1)}={0.4·10^6·12·10^{-3}}/{15·10^{-3}}=0.32$МПа.
Задача 11
Температура идеального газа понизилась от 700◦С до 350◦С. Во сколько раз при этом изменилась средняя кинетическая энергия движения молекул газа? Ответ округлить до сотых
Решение
Дано:
$T_1=700°C+273=973K$
$T_2=350°C+273=623K$
${E_1}/{E_2}-?$
Решение:
Из основ молекулярно-кинетической теории известно, что ${E_1}/{E_2}={T_1}/{T_2}$
${E_1}/{E_2}={973}/{623}=1.56$
Задача 12
При какой температуре молекулы гелия имеют такую же среднюю квадратичную скорость, как молекулы водорода при 27◦С? Ответ выразите в (◦ С).
Решение
Дано:
$t_{H_2}=27°C$
$<υ_{кв}>_{He}=<υ_{кв}>_{H_2}$
$t_{He}-?$
Решение:
Средняя квадратичная скорость молекул гелия и водорода ($He$ и $H_2$) равны соответственно: $<υ_{кв}>_{He}=√{{3RT_{He}}/{μ_{He}}}$, где $T_{He}=t_{He}+273°C$
$<υ_{кв}>_{H_2}=√{{3RT_{H_2}}/{μ_{H_2}}}$, где $T_{H_2}=t_{H_2}-273°C$
Молярные массы гелия $He$ и водорода $H_2$ равны соответственно: $μ_{He}=4·10^{-3}кг/моль; μ_{H_2}=2·10^{-3}кг/моль; T_{H_2}=27°C+273°C=300K$
$√{{3RT_{He}}/{μ_{He}}}=√{{3RT_{H_2}}/{μ_{H_2}}}⇒{3RT_{He}}/{μ_{He}}={3RT_{H_2}}/{μ_{H_2}}⇒T_{He}={T_{H_2}·μ_{He}}/{μ_{H_2}}={300·4·10^{-3}}/{2·10^{-3}}=600K$, тогда $t_{He}=T_{He}-273°C=600°C-273°C=327°C$
Задача 13
1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 3 раза. Найдите первоначальную температуру газа. Ответ выразите в (К).
Решение
Дано:
$υ=1$моль
$υ=const$
$∆T=200K$
${P_1}/{3}=P_2$
$T_1-?$
Решение:
${P_1}/{T_1} = {P_2}/{T_2}$ - изохорный.
$T_1={P_1}/{P_2}·T_2={P_1}/{P_2}·(T_1-∆T)$
$T_1=3·(T_1-200)$
$2T_1=600$
$T_1=300K$
Задача 14
Определите плотность азота при температуре 27◦С и давлении 150 кПа. Ответ округлите до десятых. Ответ выразите в (кг/м3).
Решение
Дано:
$T=27°C=300K$
$P=150$кПа
$v=2(Т_2)$
$ρ-?$
Решение:
$PV={m}/{M}·RT$
$ρ·R·T=P·M$
$ρ={P·M}/{R·T}={150·10^3·0.028}/{8.31·300}=1.7{кг}/м^3$.
Задача 15
В сосуде содержится неон при температуре −3◦С. Во сколько раз увеличится средняя кинетическая энергия теплового движения молекул неона, если его нагреть до 132◦С? В ответе запишите в(во) сколько раз(а).
Решение
Дано:
$t_1=-3+273=270К$
$T_2=132+273=405K$
${E_{к_2}}/{E_{к_1}}$
Решение:
$E_к={3}/{2}KT$.
${E_{к_2}}/{E_{к_1}}={T_2}/{T_1}={405}/{270}=1.5$
Задача 16
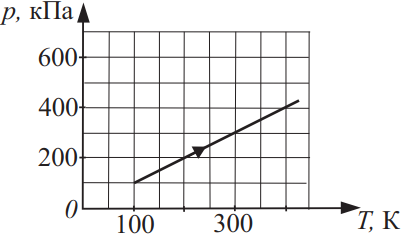
На рисунке показан график изменения давления 10 моль газа при изохорном нагревании. Найдите объём этого газа. Ответ округлите до целого, выразив в (дм3).
Решение
Дано:
$V-?$
$V=const$
$υ=10$моль
Решение:
Из уравнения Менделеева-Клайперона $pV=υRT⇒V={υRT}/{p}={10·8.31·100}/{100·10^3}=83.1дм^3$
Задача 17
В сосуде содержится водород, манометр показывает 0,5 атмосферы. Какое установится давление, если концентрацию водорода увеличить в 6 раз, а среднюю кинетическую энергию теплового движения его молекул уменьшить в 4 раза? Ответ выразите в (кПа).
Решение
Дано:
$P_1=0.5·P_{атм}$
$n_2=6·n_1$
$E_{к_2}={E_{к_1}}/{4}$
$P_{атм}=10^5$
Решение:
$\{\table\P_1={2}/{3}·n_1·E_{к_1}; \P_2={2}/{3}·n_2·E_{к_2};$ $⇒{0.5·10^5}/{P_2}={1}/{6}:{1}/{4}$.
Для 1 и 2 случая $P_2=75·10^3$Па.
Задача 18
В сосуде содержится аргон при температуре 327◦С. Какая абсолютная температура установится, если концентрацию аргона увеличить в 2 раза, а давление уменьшить в 3 раза? Ответ выразить в (K).
Решение
Дано:
$T^1_{Ар}=327+273=600K$
$n_2=2·n_1$
$P_2={P_1}/{3}$
$T_2$
Решение:
Запишем уравнение состояния газа дважды:
$\{\table\P_1=n_1·K·T_1; \P_2=n_2·K·T_2;$ $⇒T_2={T_1}/{2}={600}/{6}=100K$.
Задача 19
В закрытом сосуде под поршнем находится водяной пар при температуре 100◦С под давлением 40 кПа. Каким станет давление пара в сосуде, если объём пара в нём изотермически уменьшить в 1,5 раза за счёт движения поршня? Ответ выразите в (кПа).
Решение
Дано:
$T_1=100°С$
$P_1=40$кПа
$T=const$
$V_2={V_1}/{1.5}$
$P_2-?$
Решение:
По закону Менделеева-Клайперона $P_1·V_1=P_2·V_2⇒P_2={P_1·V_1}/{V_2}=40·1.5=60$кПа.
Задача 20
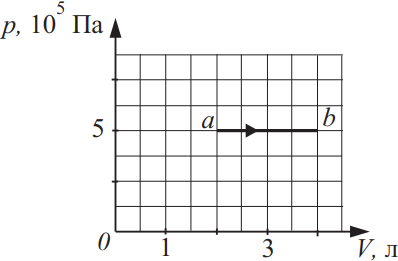
Идеальный газ в количестве 1,5 моля совершает процесс, изображённый на рисунке. Какова температура газа в состоянии b? Ответ выразите в (K), округлив до сотых.
Решение
Дано:
$v=1.5$моль
$T_в-?$
$P=const=10^5$Па
$V_a=2л$
$V_в=4л$
Решение:
По закону Менделеева-Клайперона для точки а и в составим систему: $\{\table\P·V_a=vRT_a(1); \P·V_в=vRT_в(2);$. Из (2) найдем: $T_в={5·10^5·4·10^{-3}}/{1.5·8.31}=160.45K$
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

