Задание 22. Механика (расчётная задача). ЕГЭ 2026 по физике
Средний процент выполнения: 46%
Ответом к заданию 22 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Чему равен модуль силы F, с которой двигают брусок массой m = 2 кг, при этом коэффициент трения равен $μ= 0,2$, а сила F направлена под углом $α= 30∘$ к горизонту (сила направлена вверх по горизонтали). Модуль силы трения, действующей на брусок, $F_{тр} = 2,8 $Н.
Решение
Дано:
$m=2$ кг
$μ= 0,2$
$F_{тр}=2,8$Н
$α= 30∘$
$|F| = ?$
Решение:
По закону Амантона-Кулона сила трения равна $$F_{тр}=μ N$$. Где $N$ - сила нормальной реакции опоры.
Запишем второй закон Ньютона на вертикальную ось.
$$N-mg-F*sin{α}=0$$
$$N=mg+F*sin{α}$$
Подставим полученное выражение для $N$ в выражение для силы трения и получим:
$$F={μmg-F_{тр}}/{μsin{α}}={0,2 * 20 - 2,8}/{0,2 * 0,5}=12 H$$
Ответ: 12 Н
Задача 2
Камень, подброшенный вертикально вверх упал на землю через t=1с. На каком расстоянии по горизонтали упадет камень, если его бросить с той же начальной скоростью, но под углом а=15 градусов?
Решение
Тут важно помнить, что скорости одинаковые и нужно как-то найти начальную скорость на вертикальном участке. Для этого нужно написать уравнение скоростей и выразить ее, после уже написать уравнение движения на горизонтальный участок во 2-ом случае.
Ответ : 1.25м.
Задача 3
В длинной комнате с высотой потолка H = 5.5 м один брат кидает носок в другого брата с начальной скоростью V = 20 м/с. На каком максимальном расстоянии должна находиться голова второго брата по горизонтали? Сопротивлением воздуха и размерами носка можно пренебречь, бросок делается и принимается головой второго брата на уровне h = 1.5 м от горизонтального пола.
Обоснуйте применимость используемых законов к решению задачи.
Решение
1) Изначально нужно узнать угол при наибольшей дальности полета, для этого применим формулу пути без времени. Откуда видно, что угол ограничен высотой комнаты (т.к. он меньше угла 45 градусов). угол а=26.565 градусов.
2) Чтобы найти максимальную дальность полета, необходимо записать уравнение движения на ось Х: x=xo+Vot+at^2/2 => L=V^2*sin2a/g (Время всего полета t было найдено по формуле t=2Vsina/g), L=20*20*0.8/10=32(м).
3) L=32м.
Задача 4
Поезд тормозит равнозамедленно. В начале торможения скорость поезда была равна 20 м/с. За первые 5 с скорость поезда уменьшилась на 5 м/с. Определите тормозной путь поезда.
Решение
Дано:
$υ_{0x}=20$ м/с
$ ∆t=5$с
$∆υ=5$ м/с
$υ_{к}=0$ м/с
$S-?$
Решение:
Пусть поезд двигается вдоль горизонтальной оси X, тогда координата поезда: $x=x_0+υ_{0x}t+{a_xt^2}/{2}$,
где $x_0=0$ - начальная координата, $a_x$ - проекция ускорения на ось X.
$t$ - время торможения, тогда тормозной путь $S=x-x_0=υ_{0x}t+{a_xt^2}/{2}$
Определим проекцию ускорения: $a_x={∆υ_x}/{∆t}={-∆υ}/{∆t}={-5м/с}/{5с}=-1 м/{c^2}$
Изменение проекции скорость ${∆υ_x}={-∆υ}=-5м/с$, так как за время $∆t$ скорость поезда уменьшилась на $∆υ=$5 м/с.
Найдём время торможения:
По определению проекция ускорения: $a_x={υ_к-υ_{0x}}/t$,
тогда $t={υ_к-v_{0x}}/{a_x}={0-20}/{-1}=20$с.
Тормозной путь: $S=υ_{0x}t+{a_xt^2}/{2}=20м/с·20с+{-1м/{с^2}·(20c)^2}/{2}=200$м
Ответ: 200м.
Задача 5
К потолку лифта, который движется вверх с ускорением 2 $м/с^2$, подвешен груз на пружине жёсткостью 100 Н/м. Определите растяжение пружины, если масса груза равна 0,5 кг.
Решение
Дано:
$a=2 м/{с^2}$ $k=100 Н/м$ $m=0,5 кг$
Найти: $∆l$
Решение:
Запишем 2 закон Ньютона для груза: $mg↖{-}+{F↖{-}}_{упр}=ma↖{-}$
${F}_{упр}=k∆l$
Проекция 2 закона Ньютона на вертикальную ось, направленную вверх: $-mg+k∆l=ma$ $k∆l=m(a+g)$$∆l={m(a+g)}/k=$ 0,06 м = 6 см
Задача 6
Ластик подбросили вертикально вверх со скоростью $15$ м/с. В этот же момент с высоты $3$ м начал падать без начальной скорости кусок пластилина. Через какое время они столкнутся? Ответ выразите в (с)
Решение
Уравнение движение ластика: $y=15t-(g/2)t^2=15t-5t^2$
Уравнение движения пластилина: $y=3-gt^2/2=3-5t^2$
Они столкнутся когда будут равны их координаты
$15t-5t^2=3-5t^2$
$
15t=3$
$
t=3/15=0.2$
Задача 7
Из-под машины вылетел маленький кусок грязи со скоростью $15$ м/с под углом $α$ к горизонту. Найдите максимальную высоту, на которую поднимется этот кусочек. ($sin α=3/5$, $cos α=4/5$). Ответ выразите в (м)
Решение
Запишем зависимость координаты по вертикальной направленной вверх оси y от времени t:
$y(t)=y_0+v_0sinα t-{gt^2}/2$ (начальная координата $y_0=0$)
В момент времени t_в, соответствующий верхней точке траектории, координата у принимает значение высоты полёта h:
$y(t_в)=h=v_0sinα {t_в}-{g{t_в}^2}/2$ (1)
Найдём $t_в$. В верхней точке траектории скорость тела имеет горизонтальное направление, значит вертикальная проекция скорость $v_y(t_в)=0$
$v_y(t_в)=0=v_0sinα-{g{t_в}}$, значит $t_в={v_0sinα}/g$
Подставим выражение для $t_в$ в выражение (1):
$h=v_0sinα ({{v_0sinα}/g})-g/2({{v_0sinα}/g})^2={{v_0}^2{sin}^2α}/{2g}$
$h=={{15}^2(3/5)^2}/{20}=4,05$ м
Задача 8
Масса Маши $50$ кг. Она встала на напольные весы в лифте, который движется вниз с ускорением $2 м/с^2$. Каковы будут показания весов? Ответ приведите в (кг)
Решение
Дано: $m = 50 кг$ $a = 2 м/с^2$ $m_2 = ?$
На Машу действует сила тяжести $mg$, направленная вниз, и сила нормальной реакции опоры $N$, направленная вверх. По третьему закону Ньютона, вес Маши по модулю равен $N$, поэтому будем искать именно её. Запишем 2 закон Ньютона в проекции на вертикальную ось, направленную вниз: $$ma=mg-N$$ $$N=mg-ma=m(g-a)$$ Тогда показания весов: $$m_2=N/g=m(g-a)/g={50(10-2)}/{10}=40 {кг}$$ Ответ: 40 кг
Задача 9
Брусок массой 800 г, движущийся по гладкой горизонтальной поверхности со скоростью 10 м/с, неупруго ударяется о такой же, но неподвижный брусок и теряет 3/5 своей скорости. Найдите количество теплоты, выделившейся при соударении брусков. Ответ выразите в (Дж).
Решение
Дано:
$m=0.8$кг
$υ=10$м/с
$Q-?$
Решение:
По закону сохранения импульса:${mυ_0}={mυ_1 + mυ_2}$
выходит, что скорость $υ_1 = 2/5υ_0$, а $υ_2 =3/5υ_0$
Запишем закон сохранения энергии ${mυ_0^2}/{2}={mυ_1^2}/{2}+ {mυ_2^2}/{2}+Q$
$Q={m}/{2}·( {υ_0^2}-{υ_1^2}-{υ_2^2})=19.2$Дж
Задача 10
Чему равно ускорение свободного падения на поверхности некоторой планеты, радиус которой равен радиусу Земли, но средняя плотность в 1,5 раза больше средней плотности Земли? Ускорение на Земле принять равным 10 $м/{c^2}$.
Решение
Если радиусы планет равны, то их объёмы тоже равны
Ускорение на Земле:$g_3=G{M_3}/{R_3}=G{ρ_3V}/{R_3}$
Ускорение на другой планете: $g_п=G{M_п}/{R_3}=G{1,5ρ_3V}/{R_3}$
$g_3=1,5g_п=15м/{c^2}$
Задача 11
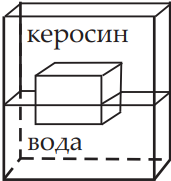
Сплошной кубик плотностью 960 кг/м3 плавает на границе раздела воды и керосина, погружаясь в воду на 5 см. Слой керосина располагается выше, чем верхняя поверхность кубика. Определите длину ребра кубика.
Ответ дайте в сантиметрах.Решение
Дано:
$h_в=0.05$м
$ρ_в=1000{кг}/{м^3}$
$ρ_к=800{кг}/{м^3}$
$ρ_{куб}=960{кг}/{м^3}$
$h_{куб}-?$
Решение:
По 2-му закону Ньютона $mg=F_{A_1}+F_{A_2}; F_{A_1}=ρ_в·g·V_в$ и $V_в=h_в·S$ - объем в воде.
$F_{A_2}=ρ_к·g·V_к$ и $V_к=h_к·S$ - объем в керосине.
Тогда условия плавания кубика: $ρ_{куб}·g·h_{куб}·S=ρ_в·g·h_в·S+ρ_к·g·h_в·S$
$h_к=h_{куб}-h_в$, тогда $ρ_{куб}·g·h_{куб}·S=ρ_в·g·h_в·S+ρ_к·g·h_к·S-ρ_к·g·h_к·S=(ρ_в-ρ_к)h_в$
$h_{куб}={h_в(ρ_в-ρ_к)}/{ρ_{куб}-ρ_к}={0.05(1000-800)}/{960-800}=6.25$см.
Задача 12
С некоторой высоты вертикально вниз бросают мяч со скоростью 4 м/с. Абсолютно упруго отразившись от горизонтальной поверхности, мяч поднимается обратно вверх на высоту 3 м. Найдите, с какой высоты тело было сброшено первоначально. Сопротивлением воздуха пренебречь. Ответ выразите в (м).
Решение
Дано:
$υ_0=4$м/с
$h_2=3$м
$h_1-?$
Решение:
По закону сохранения энергии $E_{к_1}+E_{n_1}=E_{n_2}$.
${m·υ_0^2}/{2}+mgh_1=mgh_2$.
$h_1={h_2g-{υ_0^2}/{2}}/{g}={310-{16}/{2}}/{10}=2.2$м.
Задача 13
Свободно падающее тело массой 100 г затрачивает на движение 3 с. Какова кинетическая энергия тела перед ударом о землю? Ответ выразите в (Дж).
Решение
Дано:
$υ_0=0$с
$t=3$с
$g≈10{м}/{с^2}$
$m=0.1$кг
$E_к-?$
Решение:
Кинетическая энергия определяется выражением: $E_к={mυ^2}/{2}$(1), где $υ=υ_0+gt=gt$(2) - скорость тела перед ударом о землю.
Подставим (2) в (1) и найдем $E_к$: $E_к={mg^2t^2}/{2}$(3). Подставим числовые значения в (3): $E_к={0.1·100·9}/{2}=45$Дж.
Задача 14
Чему равна средняя скорость движения автомобиля на всём пути, если первую половину пути он двигался со скоростью 70 км/ч, а вторую половину пути — со скоростью 30 км/ч? Ответ выразите в (км/ч).
Решение
Дано:
$υ_{ср}-?$
$t_1≠{t}/{2}≠t_2$
$υ_1=70км/ч$
$υ_2=30км/ч$
${S_1}/{2}={S_2}/{2}=S$
Решение:
$υ_{ср}={∆S}/{∆t}$.
$υ_{ср}={S_1+S_2}/{t_1+t_2}$.
$S=υ·t$.
$υ_{ср}={S}/{{S}/{2·70}+{S}/{2·30}}={S}/{{60S+140S}/{8400}}$.
$υ_{ср}={8400}/{200}=42{км}/ч$.
Задача 15
Парашютист опускается вниз с постоянной скоростью. В некоторый момент времени у него из кармана выпадает брелок. Определите скорость парашютиста, если известно, что брелок упал на землю через 8 с, его скорость в момент падения на землю составила 88 м/с. Ответ выразите в (м/с). Ускорение свободного падения принять равным 10 м/с$^2$
Решение
Дано:
$t=8$c
$υ_{п.б.}=88$м/с
Найти: $υ_0-?$
Решение:
Зависимость скорости брелока от времени t: $υ(t)=v_{п.б.}=υ_0+g{t};$
$υ_0=υ_{п.б.}-gt=88-10*8=8$м/с.
Начальная скорость брелока и есть скорость парашутиста $υ_0=8$м/с.
Задача 16
Пустой стакан с вертикальными стенками плавает в кастрюле с водой. Найдите массу грузика, который нужно положить в стакан, чтобы он погрузился ещё на 3 см. Площадь сечения стакана на уровне воды равна 20 см2. Ответ выразите в (г).
Решение
Дано:
$S=20см^2$
$∆h=3см$
$m-?$
Решение:
Запишем 2 условия равновесия для стакана (без груза и с грузом): $\{\table\Mg=F_{A1}; \(M+m)g=F_{A2};$;
$M$ - масса стакана
$F_{A1}$, $F_{A2}$ - сила Архимеда, действующая на стакан без груза и с грузом
$F_{A1}=ρ_в·g·V_1=ρ_в·g·h_1S$
$F_{A2}=ρ_в·g·V_2=ρ_в·g·(h_1+∆h)S$
Учтено, что объём погруженной части стакана без груза и с грузом: $V_1=h_1S$, $V_2=(h_1+∆h)S$, так как стакан имеет форму цилиндра. ( $h_1$ - глубина погружения стакана без грузика)
Система уравнений примет вид:
$\{\table\Mg=ρ_в·g·h_1S; \(M+m)g=ρ_в·g·(h_1+∆h)S;$;
Для решения системы уравнения вычтем из нижнего уравнения верхнее и получим:
$mg=ρ_в·g·∆hS$, следовательно
$m=ρ_в·∆hS=1000·3·10^{-2}·20·10^{-4}=6·10^{-2}кг=60г$
Задача 17
Пуля массой 9 г, летящая со скоростью 500 м/с, пробивает доску толщиной 3 см и вылетает со скоростью 100 м/с. Какая доля кинетической энергии пошла на преодоление силы сопротивления? Ответ выразите в (%).
Решение
Дано:
$m=9·10^{-3}кг$
$υ_1=500$м/с
$l=3·10^{-2}$м
$υ_2=100$м/с
${E_{к_1}-E_{к_2}}/{E_{к_1}}·100%-?$
Решение:
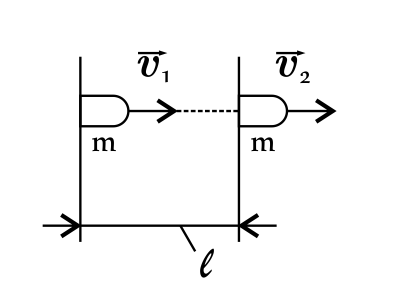
Работа средней силы сопротивления доски равна изменению кинетической энергии: $A=∆E_к$(1), или $‹F›·l={mυ_2^2}/{2}-{mυ_1^2}/{2}$(2), где $‹F›$ - средняя сила сопротивления доски. Найдем долю кинетической энергии, которая пошла на преодоление силы сопротивления, поскольку при вылете из доски, кинетическая энергия пули уменьшилась, тогда имеем: ${E_{к_1}-E_{к_2}}/{E_{к_1}}·100%={({mυ_2^2}/{2}-{mυ_1^2}/{2})·100%}/{{mυ_1^2}/{2}}={{m}/{2}(υ_1^2-υ_2^2)·100%}/{{m}/{2}υ_1^2}={(υ_1^2-υ_2^2)·100%}/{υ_1^2}$(3)
Подставим числа в (3): ${E_{к_1}-E_{к_2}}/{E_{к_1}}·100%={(25·10^4-10^4)·100%}/{25·10^4}={24·10^4·100%}/{25·10^4}=0.96·100%=96%$
Задача 18
Из пушки массой 50 кг, которая может скользить по горизонтальным рельсам, производится выстрел. Снаряд массой 5 кг вылетает под углом 60$°$ к горизонту. В результате выстрела пушка приобретает горизонтальную скорость 2 м/с. Какова дальность полёта снаряда?
Решение
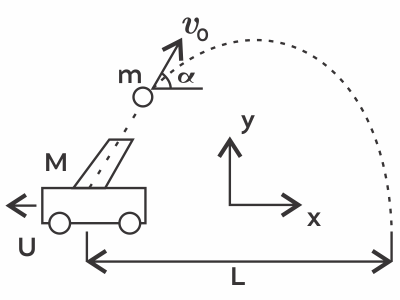
$M=50$кг
$m=5$кг
$α=60°$
$U=2$м/с
$L-?$
Запишем ЗСИ: $Mu=mv_0cosα$, откуда $v_0={Mu}/{mcosα}$
Запишем уравнения движения снаряда в проекции на оси х и у:
$\{\table\x:x(t)=x_0+v_0cosαt+{at^2}/{2}; \y:y(t)=y_0+v_0sinαt+{at^2}/{2};$
Выберем $x_0=0, y_0=0, a_x=0, a_y=-g$
$\{\table\x(t)=v_0cosαt; \y(t)=v_0sinαt-{gt^2}/{2};$
Время движения $τ$. $y(τ)=0; v_0sinατ-{gτ^2}/{2}$, откуда $τ={2v_0sinα}/{g}$
$y(τ)=L; v_0cosα·{2v_0sinα}/{g}={v_0^2sin2α}/{g}$
$L=({M}/{m})^2{u^2sin^2α}/{gcos^2α}=({M}/{m})^2{2u^2}/{g}tgα≈138.6≈139$м
Задача 19
Деревянный шарик массой 100 г падает с высоты 3 м. Отношение скорости шарика до удара к скорости шарика после удара равно двум. Найдите выделившееся при ударе количество теплоты.
Решение
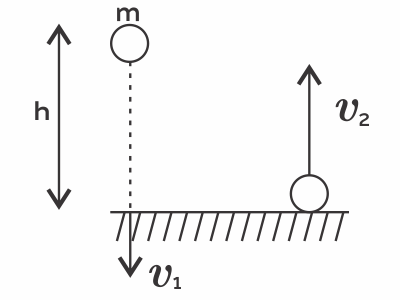
$m=0.1 кг, h=3$
Найдем скорость $v_1$ перед ударом по ЗСЭ: $mgh={mv_1^2}/{2}⇒v_1=√{2gh}$
По условию $v_2={v_1}/{2}={√{2gh}}/{2}$
Кинетическая энергия после удара ${mv_2^2}/{2}$
$Q={mv_1^2}/{2}-{mv_2^2}/{2}=mgh-{mgh}/{4}={3}/{4}mgh=2.25$Дж
Задача 20
Во сколько раз угловая скорость секундной стрелки больше угловой скорости часовой стрелки?
Решение
Угловая скорость при вращении определяется по формуле: $ω = {2π} / {T}$. Период вращения секундной стрелки равен $60$ с, часовой — $12$ ч = $43200$ с. Отношение угловых скоростей равно обратному отношению периодов: $720$.
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

