Задание 19. Измерительные приборы. Снятие показаний. ЕГЭ 2026 по физике
Средний процент выполнения: 77%
Ответом к заданию 19 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
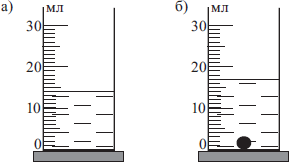
При проведении лабораторной работы ученик с помощью мерной мензурки измеряет уровень жидкости, с помещённым в неё грузиком и без. Определите объём грузика, если погрешность прямого измерения объёма в мензурке составляет половину цены деления мензурки. Ответ:(_$±$ _)мл (ответ написать слитно без $±$).
Решение
Для того, чтобы найти объём грузика, необходимо найти разность двух показаний объёма мензурки:
$V_1=14,0±0,5$, $V_2=17,0±0,5$
$V_{гр}=V_2-V_1$
если результат косвенного измерения вычисляется как сумма или разность результатов прямых измерений, то погрешности складываются: 0,5+0,5=1
$V_{гр}=3±1$
Задача 2
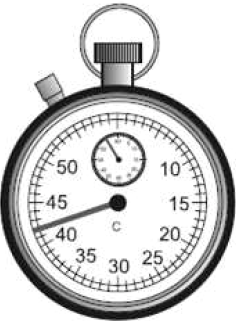
Каковы показания секундомера, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в (___ ± ___) с.
Решение
Цена деления$={50-45}/{5}=1; {ц.д.}/{2}={1}/{2}=0.5c$
Тогда показания прибора: $t=(42±0.5)c$
Задача 3
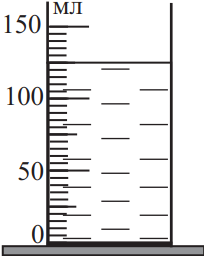
При определении массы воды, налитой в мензурку, ученик при помощи мензурки измерил объём воды. Запишите в ответ массу воды в граммах с учётом погрешности измерений (без пробелов). Погрешность измерения объёма равна половине цены деления мензурки. Ответ: (_ ± _) г.
Решение
Определим значение погрешности прямого измерения $∆V={V'}/{2}={5}/{2}=2.5г$. Тогда: $125±2.5г$. Количество знаков после запятой в измеренной величине должно совпадать с количеством знаков после запятой в значении погрешности. Поэтому $125.0±2.5г$
Задача 4
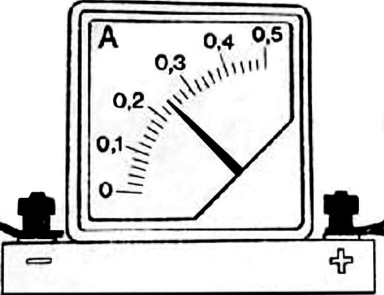
Что показывает амперметр с учётом абсолютной погрешности? Абсолютную погрешность принять равной половине цены деления прибора. Формат ответа: результат измерения и погрешность без пробелов и других разделительных знаков.
Решение
Цена деления$={0.3-0.2}/{5}={0.1}/{5}=0.02A; {ц.д.}/{2}={0.02}/{2}=0.01A$. Тогда имеем: $(0.24±0.01)A$
Задача 5
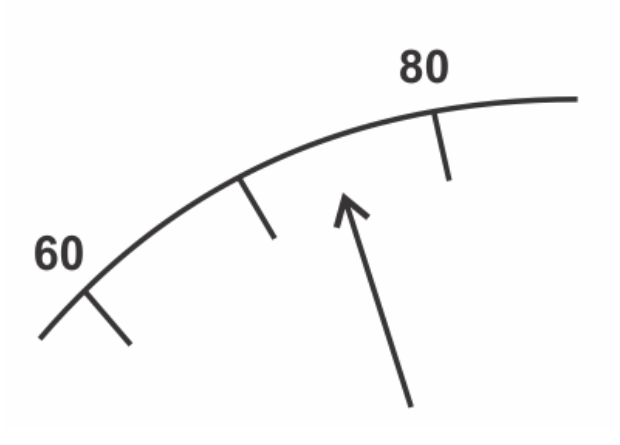
Запишите показания спидометра с учётом его погрешности, равной половине цены деления. Ответ: (_ ± _) км/ч. Значение величины и погрешность запишите слитно (без ±)
Решение
По рисунку видно, что стрелка ближе к 70, чем к 80 км/ч.
Погрешность измерения принимается за половину цены деления, а так как цена деления 10 км/ч, то показания спидометра (70 ± 5) км/ч.
Задача 6
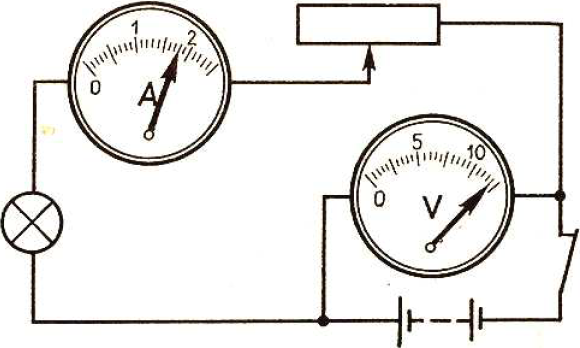
Каковы показания амперметра, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в(___ ± ___) А.
Решение
Цена деления$={2A-1A}/{10}=0.1A; {ц.д.}/{2}={0.1A}/{2}=0.05A$
Тогда показания алтерметра равны: $(1.80±0.05)А$
Задача 7

На рисунке показана шкала универсального прибора, измеряющего величину атмосферного давления, температуру и влажность. Какова относительная погрешность показания шкалы барометра, проградуированной в гПа, если абсолютная погрешность равна цене деления шкалы. Ответ выразите в (%) и округлите до десятых.
Решение
Относительная погрешность $ε={∆p}/{p_{пр}}·100%$, где $∆p={ц.д.}={{(1000-950)}/{10}}={5}гПа$.
Показания прибора барометра равны: $p_{пр}=1050гПа$, тогда $ε={5·100%}/{1050}≈0.5%$
Задача 8
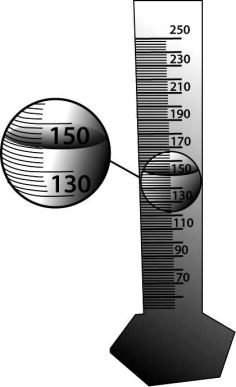
Для проведения опыта ученик налил воду в мензурку. Шкала мензурки проградуирована в миллилитрах (мл). Погрешность измерений объёма равна цене деления шкалы мензурки. Чему равен объём налитой учеником воды? Ответ: (__ ± __) мл.
Решение
Цена деления мензурки$={150-130}/{10}={20}/{10}=2мл$
Значит, объем налитой учеником воды равен: $V=(150±2)мл$
Задача 9

На фотографии представлена электрическая схема для определения сопротивления резистора. По показаниям приборов определите показания вольтметра с учётом погрешности, равной цене деления прибора. Ответ: (__ ± __) В.
Решение
Цена деления$={4-3}/{5}={1}/{5}=0.2B$
Тогда показания вольтметра равны: $(3.2±0.2)В$
Задача 10

Какую температуру показывает термометр, если погрешность прямого измерения равна половине цены деления прибора? Ответ: ( ± ) ◦ C, использовать точку, но не запятую как знак-разделитель, например 9.90.1 .
Решение
Цена деления$={40°С-30°С}/{10}={10°С}/{10}=1°С; {ц.д.}/{2}={1°С}/{2}=0.5°С$
Тогда показания термометра равны: $(26±0.5)°С$
Задача 11
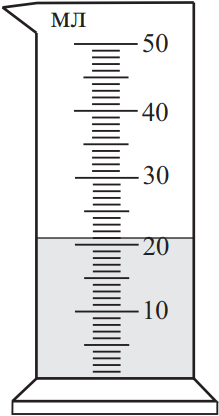
Каков объём воды в измерительном цилиндре, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в (___ ± ____) мл.
Решение
Находим погрешность как половину цены деления и получаем 0.5. Соответственно записываем показание прибора с одной цифрой после запятой, чтобы это совпадало с записью погрешности.
Задача 12
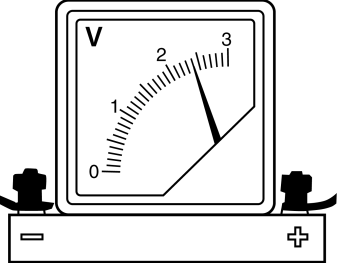
Что показывает вольтметр с учётом абсолютной погрешности? Принять абсолютную погрешность равной половине цены деления шкалы прибора.
В ответе запишите результат измерения с погрешностью без пробелов и других разделителей .Решение
Цена деления$={3-2}/{10}={1}/{10}=0.1B; {ц.д.}/{2}={0.1}/{2}=0.05B$. Тогда имеем: $(2.40±0.05)B$. Согласно правилу записи ответа с погрешностью, результат измерения и погрешность должны иметь одинаковое количество знаков после запятой.
Задача 13
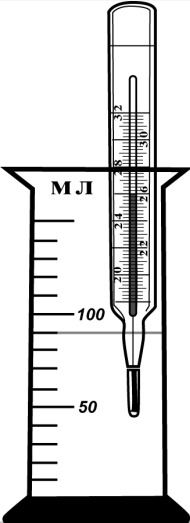
Запишите величину объёма с учётом погрешности, если погрешность равна половине цены деления. Ответ: (_ ± _) мл.
Решение
$∆V={V_1}/{2}={10}/{2}=5$мл (погрешность измерения половина цены деления). Запишем ответ исходя из рисунка $V=90$мл.
Задача 14
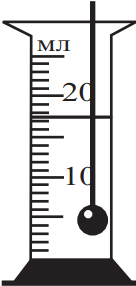
Запишите величину объёма, которая измеряется в данном эксперименте. Ответ: (_ ± _) мл.
Решение
Как известно, погрешность - это половина цены деления, где $V={V'}/{2}={1}/{2}=0.5$. Исходя из рисунка, определим объем и запишем ответ: $17.5±0.5$мл.
Задача 15
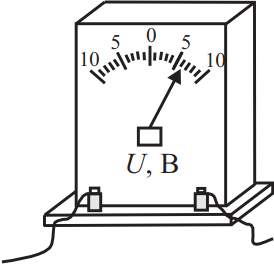
Запишите результат измерения электрического напряжения, учитывая, что погрешность равна половине цены деления. Укажите показание и погрешность. Ответ: (_ ± _) В.
Решение
Учитывая, что погрешность половины цены деления, определим ее: $∆U={1}/{2}=0.5B$. Запишем ответ, исходя из того, что прибор регестрирует $6В$: $6±0.5$.
Задача 16

С помощью амперметра проводились измерения силы тока на участке электрической цепи. Чему равна сила тока с учётом погрешностей измерений, если погрешность прямого измерения составляет половину цены деления прибора, а его класс точности равен 0,5 (т.е. инструментальная погрешность составляет 0,5% от верхнего предела измерений данной шкалы амперметра)? Ответ: (_ ± _) А.
Решение
Определим погрешность прибора: если верхняя граница равна 10А, то инструментальная равна: $∆x_{пр}={10·0,5}/100=0,05$.
Погрешность измерения равна половина цены деления $∆x_{изм}=0,25$.
$∆x=∆x_{изм}+∆x_{пр}=0,05+0,25=0,3$.
$x=7.5±0.3$
Задача 17
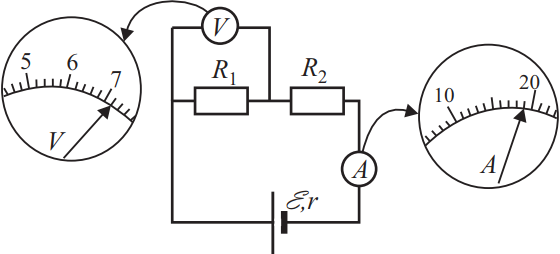
Ученик собрал электрическую цепь, состоящую из батарейки, двух резисторов, амперметра и вольтметра. После этого он провёл измерения напряжения на одном из резисторов и силы тока в цепи. Погрешности измерения силы тока в цепи и напряжения на источнике равны половине цены деления шкал приборов. Чему равно по результатам этих измерений значение напряжения на резисторе R1? Ответ: (_ ± _) В.
Решение
$U=U'+∆U; ∆U={0.2}/{2}=0.1 В$(половина цены деления). Запишем ответ $U'=7.2B$ как сумму, действующего измерения и погрешности: $7.2±0.1$.
Задача 18
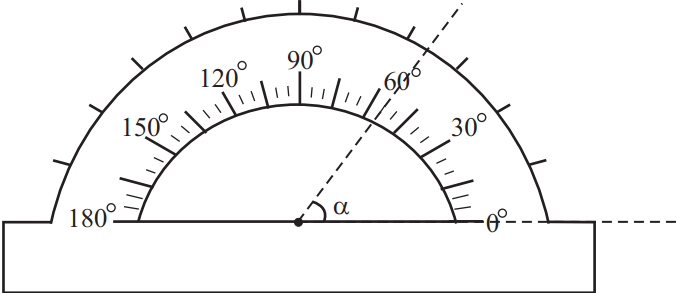
Запишите величину угла с учётом погрешности. С точностью до десятых. Ответ: (_ ± _)◦.
Решение
Найдем погрешность, как половину цены деления ${5}/{2}=2.5°$. Тогда, исходя из графика получим: $55±2.5$.
Задача 19

Найдите длину проволоки, если погрешность прямого измерения составляет половину цены деления линейки, изображённой на рисунке. Ответ: (_ ± _) см.
Решение
Погрешность измерения равна половине цены деления ${0.5}/{2}-0.25$, тогда длина проволоки $23.00±0.25$см.
Задача 20
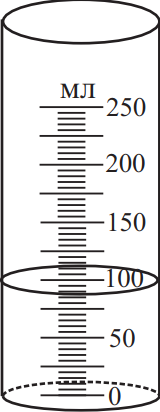
По рисунку определите объём жидкости с учётом погрешности измерения, равной половине цены деления. Ответ: (_ ± _) мл.
Решение
По измерению проведенному измерим погрешность половины цены деления 2.5: $87.5±2.5$мл.
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

