Задание 20. Выбор установки для проведения опытов. ЕГЭ 2026 по физике
Средний процент выполнения: 88.2%
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Протон и α-частица влетели в камеру Вильсона с одинаковой скоростью перпендикулярно вектору магнитной индукции. По каким признакам исследователь может сказать, где трек протона, а где — α-частицы?
- По радиусу трека. Радиус траектории движения протона больше радиуса траектории движения α-частицы.
- Протон «свернёт» влево, а α-частица — вправо.
- По толщине трека. У α-частицы толщина трека больше.
- Трудно предсказать, так как не указано направление вектора магнитной индукции.
Решение
Поскольку протон $↙{1}↖{1}p$ и $α$-частица $↙{2}↖{4}α$ отличаются зарядовыми $Z$ и массовыми $A$ числами, то исследователь может сказать, где трек протона, а где трек $α$-частицы по следующим признакам:
1) По радиусу трека. Радиус траектории движения протона больше радиуса траектории $α$-частицы, т.к. радиус трека зависит как от заряда частицы $q$, так и от ее массы $m$: $R={mυ}/{qB}$.
3) По толщине трека. У $α$-частицы толщина трека больше.
Задача 2
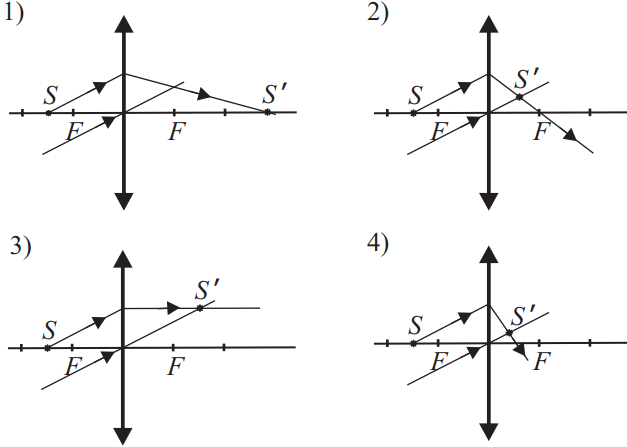
Ученик построил изображение точки, лежащей на главной оптической оси собирающей линзы с фокусным расстоянием F. Точка находится на расстоянии 1,5F от линзы. Укажите номер правильного рисунка.
Решение
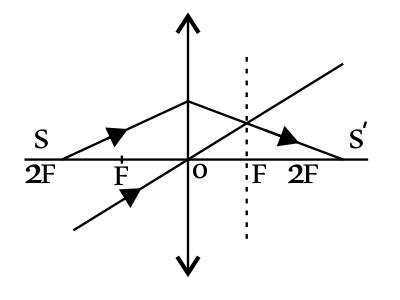
Чтобы построить изображение точки, нужно взять луч и направить его произвольно на линзу. Построить побочную оптическую ось параллельно лучу, происходящую через оптический центр. В том месте, где произойдет пересечение фокальной плоскости и побочной оптической оси, и будет побочный фокус, через который должен пройти после преломления произвольно направленный луч. Изображение точки будет находиться там, где этот луч пересечется с главной оптической осью.
Задача 3
В таблице приведены результаты измерений силы сопротивления движению тела в жидкости в зависимости от скорости тела. Как зависит сила сопротивления от скорости? Выберите все верные утверждения.
| V, м/с | 3 | 5 | 7 | 10 |
| F, H | 500 | 1300 | 2720 | 5550 |
- увеличивается пропорционально скорости
- увеличивается пропорционально квадрату скорости
- не зависит от скорости
- с ростом скорости сила сопротивления растёт
- с ростом скорости сила сопротивления уменьшается
В ответ запишите номера выбранных утверждений.
Решение
Анализируя таблицу, очевидно, что с ростом скорости тела, увеличивается и сопротивление, а так же можно сказать, пропорционально скорости $υ^2∼F$.
Задача 4
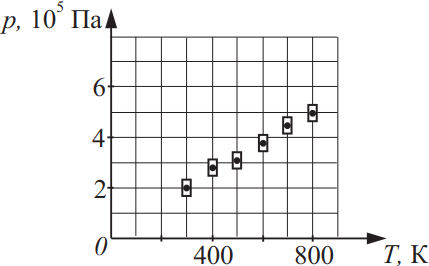
На рисунке показаны результаты измерения давления постоянной массы разреженного газа при повышении его температуры. Погрешность измерения температуры T = ±10 К, давления ∆p = ±2 · 104 Па. Количество вещества газа равно 0,4 моль. Какой объём занимает газ? Ответ выразите в (л) и округлите до целых.
Решение
Дано:
$T=±10K$
$∆p=±2·10^{4}Па$
$v=0.4моль$
$R=8.31$Дж/моль·с
$V-?$
Решение:
Запишем уравнение Менделеева-Клайперона: $pV=vRT$(1), откуда $V={vRT}/{p}$(2) - объем газа. Возьмем точку на графике с координатами, например, $p=2·10^{5}Па$ и $T=300K$, тогда имеем: $V={0.4·8.31·300}/{2·10^5}=486·10^{-5}=486·10^{-2}=4.86л≈5л$
Задача 5
Чтобы собрать экспериментальную установку для исследования зависимости силы электрического тока в резисторе от напряжения на его концах, школьник взял амперметр, ключ, соединительные провода, источник тока, резистор. Какие две позиции из приведённого ниже перечня оборудования необходимо дополнительно использовать для составления комплектации для проведения этого эксперимента?
- конденсатор
- реостат
- лампочка
- диод
- вольтметр
В ответ запишите номера выбранных предметов.
Решение
Необходим реостат для изменения сопротивления и вольтметр для измерения, питающего напряжения на его концах.
Задача 6
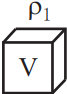
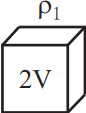
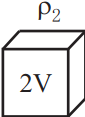
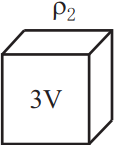
Ученику необходимо экспериментально проверить, зависит ли выталкивающая сила от плотности ρ погружаемого в воду тела. Какие два из указанных тел можно использовать для такой проверки?
В ответ запишите номера выбранных тел.
Решение
Для проверки зависимости силы Архимеда от плотности тела необходимо выбрать два тела с разными плотностями, но с одинаковыми объёмами. Пожходят 2 и 3.
Задача 7
При изучении фотоэффекта увеличили интенсивность падающего монохроматического света. Что можно сказать об изменении максимальной скорости фотоэлектронов?
- не изменится
- возрастёт
- уменьшится
- фотоэлектроны не вылетят
Решение
Запишем уравнение Эйнштейна для фотоэффекта: $hv=A_{вых}+{mυ^2}/{2}$ или ${hc}/{λ}=A_{вых}+{mυ^2}/{2}$. Мы видим, что интенсивность в состав данных формул не входит и максимальная скорость фотоэлектронов зависит от частоты падающего света или от длины волны падающего света, а от интенсивности падающего света не зависит.
Задача 8
Имеются два железных стержня А и В. При поднесении последовательно каждого конца стержня А к какому-либо концу стержня В возникает сила притяжения. Выберите два правильных варианта ответа.
- А – не магнит, В – магнит
- оба стержня не магниты
- оба стержня магниты
- данных эксперимента не достаточно
- А – магнит, В – не магнит
В ответ запишите номера выбранных утверждений.
Решение
Так как стержень А не в одном из случаев не отталкивается, очевидно, что А не магнит, а В - магнит, или наоборот.
Задача 9
Чтобы собрать экспериментальную установку для определения мощности, выделяемой на резисторе R при заданной силе тока, школьник взял источник тока, вольтметр, ключ, соединительные провода и резистор R. Какие две позиции из приведённого ниже перечня оборудования необходимо дополнительно использовать при составлении комплектации для проведения этого эксперимента?
- конденсатор
- лампочка
- реостат
- диод
- амперметр
В ответ запишите номера выбранных предметов.
Решение
Для проведения опыта необходим реостат. Для изменения $R_{вх}$ и амперметр измерение действующей силы тока.
Задача 10
В таблице зафиксированы значения силы притяжения заряженных тел при разных расстояниях между ними. Какой вывод о связи силы и расстояния можно сделать исходя из этой таблицы?
| r, см | 1 | 2 | 4 | 10 |
| F, H | 10−8 | 2,3 · 10−9 | 0,6 · 10−9 | 10−10 |
- сила уменьшается с увеличением расстояния
- сила очень мала и её можно не учитывать
- зависимость не прослеживается
- при r больше 10 см сила обращается в 0
Решение
Исходя из данных таблицы и формулы силы Кулона: $F_к=K{|q_1|·|q_2|}/{r^2}$ можно сделать очевидный вывод, сила уменьшается с увеличением расстояния.
Задача 11
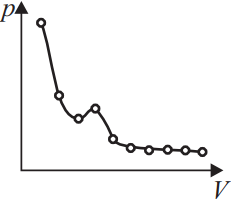
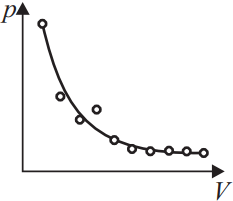
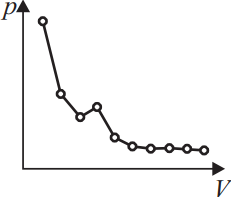
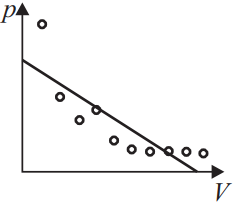
При исследовании зависимости давления газа от объёма были получены некоторые данные. Какой график правильно проведён по экспериментальным точкам?
Решение
Графики 1 и 3 неверны, т.к. при построении следует проводить плавную линию, так, чтобы по разные стороны, количество точек было одинаковым. Правильный ответ 2, на нем меньший разброс, а одна выпавшая точка это случайный промах.
Задача 12
Исследовалась зависимость напряжения на участке цепи от сопротивления этого участка. Результаты измерений представлены в таблице.
| R, Ом | 0 | 1 | 2 | 3 | 4 | 5 |
| U, В | 0 | 1,8 | 4,2 | 5,8 | 8,4 | 11,6 |
Погрешности измерений величин U и R равнялись соответственно 0,2 В и 0,5 Ом. Чему равна сила тока на этом участке цепи? Ответ укажите в амперах с точностью до 0,5 А. Ответ выразите в (А).
Решение
Рассчитаем для каждого измерения величину силы тока $(J={U}/{R})$ и усредним получившиеся значения.
| R, Ом | 0 | 1 | 2 | 3 | 4 | 5 |
| U,B | 0 | 1.8 | 4.2 | 5.8 | 8.4 | 11.6 |
| J,A | - | 1.8 | 2.1 | 1.93 | 2.1 | 2.32 |
Среднее значение силы тока равно: $‹J›={(1.8+2.1+1.93+2.1+2.32)A}/{5}={10.25A}/{5}=2.05A≈2.0A$
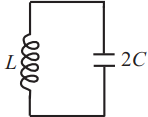
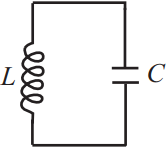
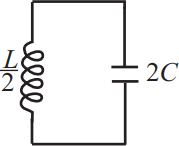
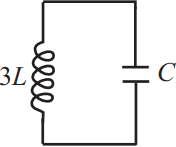
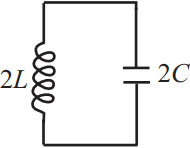
Задача 13
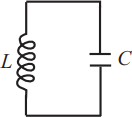
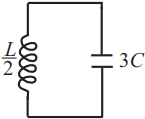
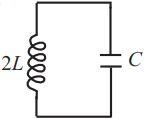
Ученик изучает зависимость периода свободных колебаний в колебательном контуре от индуктивности катушки. Какие две схемы он должен для этого использовать? В ответ запишите номера выбранных схем.
Решение
Период колебаний колебательного контура определяется выражением: $T=2π√{LC}$, где $C$ - емкость конденсатора, $L$ - индуктивность катушки.
Таким образом, чтобы изучить зависимость Т от L, надо, чтобы емкость конденсатора была неизменной, а индуктивность менялась. Этим условиям соответствуют схемы 1 и 3.
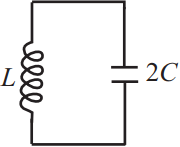
Задача 14
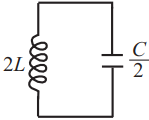
Ученик изучает зависимость периода свободных колебаний в колебательном контуре от ёмкости конденсатора. Какие две схемы он должен для этого использовать? В ответ запишите номера выбранных схем.
Решение
Период колебаний колебательного контура определяется выражением: $T=2π√{LC}$, где $C$ - емкость конденсатора, $L$ - индуктивность катушки.
Таким образом, чтобы изучить зависимость Т от С, надо, чтобы индуктивность была неизменной, т.е. $L=const$, а емкость конденсатора менялась. Этим условиям соответствуют схемы 1 и 5.
Задача 15
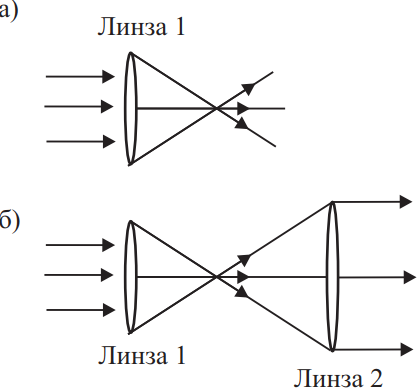
Ученик проводит опыты с двумя линзами, направляя на них параллельный пучок света. Ход лучей в этих опытах показан на рисунке. Согласно результатам этих опытов, оптическая сила второй линзы ...
- больше оптической силы первой линзы
- равна оптической силы первой линзы
- меньше оптической силы первой линзы
- не может быть определена из этого опыта
Решение
Исходя из проведенного опыта, очевидно, что меньшей оптической силой обладает 2 линза $D_2={1}/{F_1} < {1}/{F_2}=D_2$.
Задача 16
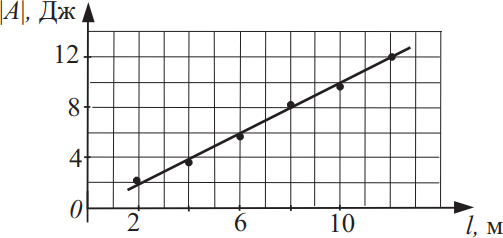
Брусок массой 250 г тянут по горизонтальной шероховатой поверхности, прикладывая к нему горизонтально направленную силу. На графике приведена найденная экспериментально зависимость модуля работы A силы сухого трения, действующей на брусок, от пройденного пути l.
Используя этот график, из приведённого ниже списка выберите два верных утверждения. В ответ запишите номера выбранных утверждений.
- Коэффициент трения бруска о поверхность равен 0,4.
- Брусок движется равноускоренно.
- Если уменьшить массу бруска в 2 раза, он станет двигаться вдвое быстрее.
- Когда пройденный бруском путь станет равным 10 м, работа силы сухого трения, действующей на брусок, станет отрицательной и будет равна −20 Дж.
- Модуль силы, приложенной к бруску, равен 1 Н.
Решение
Дано:
$m=0.25$кг
$A=2⇔l=2$м
Решение:
Тогда $F_{тр}={A}/{S}; μ·mg={A}/{S}$. $μ={A}/{mg·S}={2}/{0.25·10·2}={1}/{2.5}=0.4$
$F=μmg=0.4·0.25·10=1H$.
Задача 17
Ученик проводил опыты с двумя разными резисторами, измеряя значения силы тока, проходящего через них при разных напряжениях на резисторах, и результаты заносил в таблицу.
| U, В | 0 | 1 | 2 | 3 |
| I1, А | 0 | 0,3 | 0,6 | 0,8 |
| I2, А | 0 | 0,25 | 0,55 | 0,75 |
Выберите одно верное утверждение.
Прямая пропорциональная зависимость между силой тока в резисторе и напряжением на концах резистора ...- выполняется только для первого резистора
- выполняется только для второго резистора
- выполняется для обоих резисторов
- не выполняется для обоих резисторов
Решение
Решение:
Закон Ома $\{\table\I_1={U_1}/{R_I}, I_2={U_2}/{R_I}⇒{1}/{0.3}≠{3}/{0.8}; \I_1={U_1}/{R_II}, I_2={U_2}/{R_II}⇒{1}/{0.25}≠{2}/{0.55};$.
Закон Ома не выполняется для обоих резисторов.
Задача 18
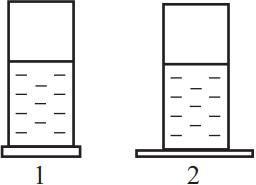
Ученик налил в два одинаковых сосуда одно и то же количество разной жидкости, находящейся при комнатной температуре, и в результате эксперимента установил, что во втором сосуде жидкость испарится быстрее. Из этого ученик сделал вывод, что скорость испарения жидкости ...
- увеличивается с увеличением её температуры
- зависит от площади её поверхности
- зависит от её плотности
- зависит от её количества
Решение
Из теории об испарении жидкости можем сказать, что в данном опыте скорость испарения зависит от плотности.
Задача 19

Выберите два верных ответа с учётом рисунка, на котором изображено тело, перемещающееся с постоянной скоростью по горизонтали.
- сила трения равна 3,5 H
- силу трения невозможно определить по рисунку
- сила трения равна 3 H
- сила трения равна 4,5 H
- это сила трения скольжения
Решение
Так как $υ=const$Па динамометра, сила трения равна 3.5Н(1). Это сила трения скольжения (5).
Задача 20
Человек рассматривает два предмета. Первый находится вблизи глаза, второй — на значительном расстоянии. В каком случае оптическая сила хрусталика глаза больше?
- одинаково в обоих случаях
- в первом
- во втором
- оптическая сила зависит от освещённости
Решение
Чем ближе предмет, тем меньше фокусное расстояние оптической системы глаза (благодаря аккомодации). Оптическая сила есть величина, обратная фокусному расстоянию $D={1}/{F}$, т.е. при рссмотрении близких предметов оптическая сила больше, чем при рассмотрении далеких.
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ