Задание 14. Электродинамика. Анализ физических процессов. ЕГЭ 2026 по физике
Средний процент выполнения: 51.1%
Ответом к заданию 14 по физике может быть целое число или конечная десятичная дробь.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1

На рисунке приведены опыты, демонстрируемые учителем на уроке физики. На основании анализа этих опытов выберите два верных утверждения.
- Индукционный ток возникает при изменении магнитного потока, пронизывающего контур.
- Возникновение индукционного тока происходит при различных способах изменения магнитного потока.
- Сила индукционного тока зависит от скорости изменения магнитного потока.
- Направление индукционного тока не зависит от способа изменения магнитного потока.
- При деформации катушки, помещённой в магнитное поле, стрелка гальванометра отклоняется.
Решение
1) Согласно явлению электромагнитной индукции, индукционный ток возникает при любом изменении магнитного потока, пронизывающего контур (подходит).
2) Не имеет значения каким образом изменяется магнитный поток, пронизывающий контур, в любом случае изменения магнитного потока в контуре возникает индукционный ток.
Задача 2
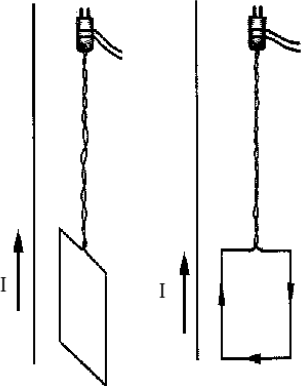
На рисунке показано поведение рамки с током, помещённой вблизи бесконечно длинного прямолинейного проводника с током. На основании анализа данного опыта выберите два верных утверждения.
- Токи, текущие в одинаковых направлениях, отталкиваются.
- Рамка устанавливается таким образом, чтобы магнитная индукция поля тока была перпендикулярна её плоскости.
- При расположении рамки в одной плоскости с проводником её энергия становится равной нулю.
- Левая сторона рамки от проводника с током отталкивается, а правая — притягивается.
- В магнитном поле тока на рамку действует вращающий момент.
Решение
1) Токи, текущие в одинаковых напрвлениях, притягиваются (не подходит).
2) Рамка устанавливается таким образом, чтобы магнитная индукция поля тока была перпендикулярна ее плоскости (подходит).
5) Поскольку рамка поворачивается, то в магнитном поле тока на рамку действует вращающий момент: $M=JSB·sinα$ (подходит).
Задача 3
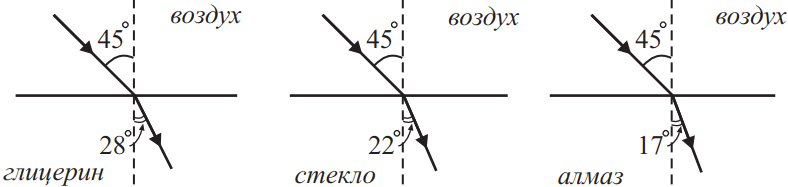
Ученик, изучая преломление света, пускает лазерный луч на границы раздела «воздух–алмаз», «воздух–стекло», «воздух–глицерин». (sin 28◦ = 0,47; sin 22◦ = 0,37; sin 17◦ = 0,29). Выберите из предложенного ниже списка два утверждения, соответствующих результатам опыта.
- Угол преломления не зависит от свойств преломляющей среды.
- Показатель преломления алмаза наибольший.
- Показатель преломления стекла наименьший.
- Показатель преломления глицерина равен 1,5.
- Угол преломления не зависит от угла падения.
Решение
Исходя из проведенного опыта, угол преломления алмаза наибольший, т.к. $n_{ал}$ - показатель наибольший. А показатель глицерина ${n_г}/{n_в}={sin45°}/{sin28}=1.5$.
Задача 4
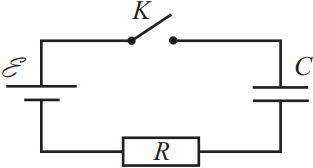
Конденсатор подключён к идеальному источнику тока последовательно с резистором R = 10 кОм. В момент времени t = 0 ключ замыкают. В этот момент конденсатор полностью разряжен. Результаты измерений силы тока в цепи, выполненных с точностью ±0,5 мкА, представлены в таблице.
| t, c | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| I, мкА | 300 | 110 | 40 | 15 | 5 | 2 | 1 |
Выберите два верных утверждения о процессах, наблюдаемых в опыте.
- Ток через резистор в процессе наблюдения увеличивается.
- Через 6 с после замыкания ключа конденсатор полностью зарядился.
- ЭДС источника тока составляет 3 В.
- В момент времени t = 4 с напряжение на резисторе равно 0,3 В.
- В момент времени t = 4 с напряжение на конденсаторе равно 2,95 В.
Решение
1) Ток через резистор, судя по таблице, в процессе наблюдения уменьшается (не подходит).
2) Через 6с после замыкания ключа конденсатор зарядился не польностью, т.к. при полной зарядке сила тока в цепи была бы равна нулю (не подходит).
3) По закону Ома: $J={ε}/{R}⇒ε=J·R=300·10^{-6}·10^4=3B$ (подходит).
4) В момент времени $t=4c$, напряжение на резисторе равно: $U_R=J·R=5·10^{-6}·10^4=5·10^{-2}=0.05B$ (не подходит).
5) Напряжение на конденсаторе в момент времени $t=4с$: $U_c=ε-U_R(4c)=3-0.05=2.95B$ (подходит).
Задача 5
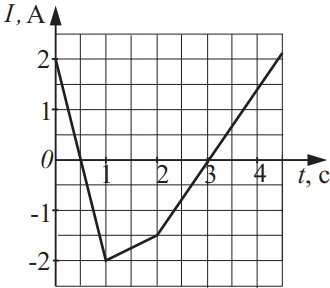
В катушке индуктивностью 3 мГн сила тока I зависит от времени t, как показано на графике, изображённом на рисунке. Используя этот график, из приведённого ниже списка выберите два правильных утверждения о процессах, происходящих в катушке.
- Модуль ЭДС самоиндукции, возникающей в катушке, максимален в интервале времени от 0 с до 1 с.
- В интервале времени от 0 с до 0,5 с в катушке накапливается энергия магнитного поля, равная 6 мДж.
- Модуль ЭДС самоиндукции, возникающей в катушке, в интервале времени от 2 с до 3 с равен 4,5 мВ.
- Модуль ЭДС самоиндукции, возникающей в катушке, максимален в интервале времени от 1 с до 2 с.
- Магнитное поле около катушки минимально в интервале времени от 0 с до 1 с.
Решение
Дано:
$α=3·10^{-3}$Гн
$I(t)$
Решение:
Из графика, модуль ЭДС самоиндукции в интервале от 0 до 1 - максимален, т.к. максимальная $∆I'=I_2-I_1$, а в интервале 2-3 $ε_i=-L{∆I}/{∆t}=3·{1.5}/{1}=4.5$мВ.
Задача 6
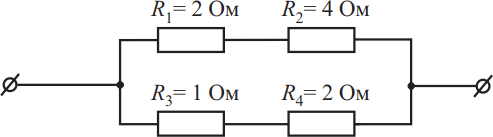
В каком из четырёх резисторов при протекании тока выделится большее количество теплоты и по какому участку цепи протекает больший ток? Из предложенного перечня выберите два утверждения, соответствующих экспериментальным наблюдениям.
- Большее количество теплоты выделится в резисторах R1 и R4.
- Большее количество теплоты выделится в резисторе R4.
- Большее количество теплоты выделится в резисторе R2.
- Ток в верхнем и нижнем участках цепи протекает одинаковый.
- Наибольший ток протекает через сопротивления R3, R4, то есть по нижнему участку цепи.
Решение
Согласно закону Ома $J={U}/{R}$(1). При одинаковом напряжении $U$, сопротивление верхнего участка цепи $R_{12}=R_1+R_2=2+4=6$Ом, сопротивление нижнего участка цепи $R_{34}=R_3+R_4=1+2=3$Ом. Из закона Ома следует, что чем меньше сопротивление, тем больше сила тока и наоборот, поэтому наибольший ток протекает через сопротивления $R_3,R_4$, то есть по нижнему участку цепи. Количество теплоты, которое выделится в резисторе, определяется законом Джоуля-Ленца: $Q=J^2Rt=JUt$, т.к. из него видно, что $Q$ тем больше, чем больше сила тока $J$, протекающего через резистор, и чем больше сопротивление резистора, поэтому большее количество теплоты выделится в резисторе $R_4=2$Ом. Хотя $R_2=4$Ом $> R_4=2$ОМ, то по нему течет ток меньший, а квадрат тока растет быстрее, чем $R$, поэтому большее $Q$ выделится в $R_4$.
Задача 7
Ученик измерял зависимость силы тока в электрической цепи от величины напряжения на концах цепи. Результаты его измерений занесены в таблицу.
| U, В | −16 | −9 | −4 | 0 | 4 | 9 | 16 |
| I, мА | 0 | 0 | 0 | 0 | 8 | 27 | 64 |
Выберите все верные утверждения на основании анализа приведённых данных.
- При напряжении больше нуля сопротивление цепи резко уменьшается.
- Цепь обладает свойством односторонней проводимости.
- При напряжении больше нуля сопротивление цепи резко возрастает.
- При силе тока 8 мА сопротивление цепи равно 2 Ом.
- При напряжении 16 В сопротивление цепи равно 0,25 Ом.
Решение
1) По закону Ома $J={U}/{R}$, откуда сопротивление $R={U}/{J}$. Тогда: $R_1={U_1}/{J_1}={4}/{8·10^{-3}}=500$Ом; $R_2={U_2}/{J_2}={9}/{27·10^{-3}}=333.3$Ом; $R_3={U_3}/{J_3}={16}/{64·10^{-3}}=250$Ом. Из данной последовательности значений сопротивлений видно, что при напряжении больше нуля сопротивление цепи резко уменьшается (подходит).
2) Из таблицы видно, что цепь обладает свойством односторонней проводимости, т.к. при отрицательных значениях напряжения, сила тока в цепи равна нулю (подходит).
3) появляется ток, значит сопротивление уменьшилось, а не возросло
4) $R=U/I=4/{0.008}=500$ Ом
5) $R=U/I=16/{0.064}=250$ Ом
Задача 8
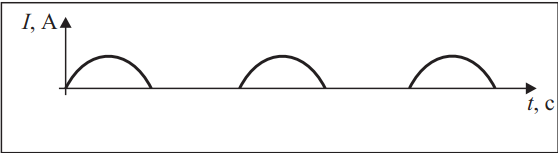
Исследуя электрическую цепь переменного тока, состоящую из амперметра, конденсатора и других элементов цепи, соединённых последовательно, ученик на экране осциллографа увидел картину, изображённую на рисунке. Известно, что осциллограмма переменного тока — синусоида. Установите соответствие между видами тока и утверждениями.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Вид тока | Утверждения |
| А) постоянный Б) переменный | 1) 1) Если эту же цепь подключить к источнику постоянного тока, то ученик увидит на экране прямую линию. 2) Если эту же цепь подключить к источнику постоянного тока, то ученик увидит на экране светящуюся точку. 3) Искажение осциллограммы произошло из-за плохих контактов, которые прерывали ток. 4) Искажение осциллограммы произошло из-за того, что в цепи был включён резистор с очень большим сопротивлением. 5) Искажение осциллограммы произошло из-за того, что в цепи был включён полупроводниковый диод. |
Решение
А) При подключении к источнику постоянного тока данной электрической цепи, ученик увидит на электроне прямую линию, т.к. $J=const$, и ток имеет какое-то числовое значение.
Б) Поскольку осциллограмма переменного тока - синусоида, а на осцилографе мы видим лишь положительную полуволну, а отрицательная полуволна синусоиды отсутствует, значит, искажение осциллограммы произошло из-за того, что в цепи был включен полупроводниковый диод, который обладает односторонней проводимостью, в частности, пропускает положительную полуволну, а отрицательную - нет.
Задача 9
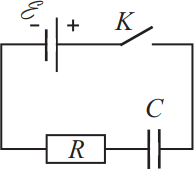
Конденсатор подключён к источнику постоянного напряжения через сопротивление R = 10 кOм, как показано на рисунке. В момент времени t = 0 ключ замыкают. Результаты измерений напряжения между обкладками конденсатора представлены в таблице. На основании схемы и данных таблицы выберите все верные утверждения.
| t, c | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U, B | 0 | 3,8 | 5,2 | 5,7 | 5,8 | 6,0 | 6,0 | 6,0 |
- Сила тока через конденсатор в момент времени t = 5 с максимальна.
- Через 5 с после замыкания ключа конденсатор полностью зарядился.
- ЭДС источника тока составляет 2,2 В.
- В момент времени t = 3 с напряжение на резисторе равно 0,3 В.
- В момент времени t = 2 с сила тока в цепи равна 520 мкА.
Решение
Дано:
$К=10$кОм
$t=0$
Решение:
1,2. Конденсатор полностью зарядится, когда напряжение на нём перестанет увеличиваться, t=5с - время полной зарядки конденсатора. 2- верно. Когда конденсатор полностью заряжен, ток в цепи не течёт, поэтому 1 - неверно.
3. ЭДС источника тока равно напряжению на нагрузке. В момент времени t>5c тока в цепи нет, значит напряжение на резисторе $U_R=0$, поэтому ЭДС равно напряжению на конденсаторе: $ε=U_C$. 3 - неверно.
4. В момент $t=3c$: $U_R=ε-U_c; U_R=6-5.7=0.3B$.4 - верно
5. Сила тока в цепи равна силе тока через резистор: $I={U_R}/R$. В момент времени t=2 c. напряжение на резисторе $U_R=ε-U_{С(t=2с)}; U_R=6-5.2=0.8$ B. Тогда $I={0.8В}/{10^4Ом}=80$ мкА. 5 - неверно
Задача 10
С использованием закона Фарадея для электромагнитной индукции ($E_{инд} = -{∆Φ}/{∆t}$) можно объяснить ... Выберите из предложенного перечня два верных утверждения.
- отклонение магнитной стрелки вблизи проводника с током
- притяжение железной детали к электромагниту
- появление тока в замкнутой катушке в процессе опускания в неё постоянного магнита
- поворот рамки с током в магнитном поле
- работу трансформатора
Решение
Исходя из закона Фарадея $ε=-{∆Ф}/{∆t}$ и школьных опытов, можно объяснить появление тока в замкнутой катушке в процессе опускания магнита ($∆Ф$) - 3, а также принцип работы трансформатора.
Задача 11
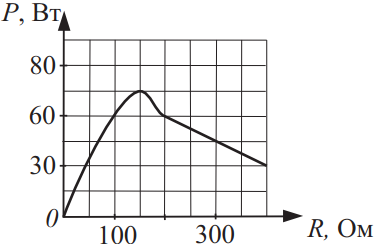
Для экспериментального изучения зависимости мощности, выделяемой во внешней части цепи, от сопротивления этой цепи была собрана замкнутая электрическая цепь. R — сопротивление внешнего участка цепи, P — выделяемая во внешней цепи мощность. Результаты измерений представлены на рисунке. Выберите два верных утверждения на основании анализа представленного графика.
- При R = 150 Ом мощность максимальная.
- При R = 150 Ом в цепи течёт максимальный ток.
- При R < 100 Ом сила тока не меняется.
- При R > 150 Ом сопротивление внешней цепи больше внутреннего сопротивления источника тока.
- При R > 150 Ом сопротивление внешней цепи меньше внутреннего сопротивления источника тока.
Решение
1) Из графика видно, что при $R=150$Ом мощность максимальная (подходит).
2) Максимальный ток в цепи течет при $R=0$ Ом исходя из закона Ома $J={ε}/{R+r}={ε}/{r}$ (не подходит).
3) При $R < 100$ Ом сила тока по закону Ома меняется в зависимости от значения $R$ (не подходит).
4) Поскольку при $r=R$ мощность, выделяемая во внешней цепи максимальна, то при $R > 150$ Ом сопротивление внешней цепи больше внутреннего сопротивления источника тока (подходит).
Задача 12
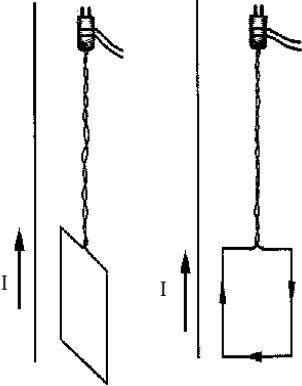
На рисунке показано поведение рамки с током, помещённой вблизи бесконечно длинного прямолинейного проводника с током. На основании анализа данного опыта выберите два верных утверждения.
- Магнитное поле тока оказывает на рамку ориентирующее действие.
- Рамка устанавливается так, что её магнитный момент сонаправлен с магнитной индукцией поля тока.
- Токи, текущие в противоположных направлениях, притягиваются.
- На противоположные вертикальные стороны рамки действуют одинаковые силы Ампера.
- При расположении рамки в одной плоскости с проводником её энергия становится максимальной.
Решение
1) Магнитное поле тока оказывает на рамку ориентирующее действие, т.к. рамка поворачивается (подходит).
2) Рамка устанавливается та, что ее магнитный момент сонаправлен с магнитной индукцией поля тока: $M↖{→}=JS{B}↖{→}·sinα$ (подходит).
Задача 13
Ученик провёл эксперимент по изучению электрического сопротивления металлического проводника, причём в качестве проводника он использовал железные и алюминиевые проволоки разной длины и толщины. Результаты экспериментальных измерений площади поперечного сечения S и длины l проволоки, а также электрического сопротивления R представлены в таблице.
| № опыта | Материал | S, мм2 | l, м | R, Ом |
| 1 | алюминий | 0,1 | 1,6 | 0,48 |
| 2 | алюминий | 0,2 | 6,4 | 0,96 |
| 3 | железо | 0,1 | 1,6 | 2,1 |
| 4 | железо | 0,2 | 1,6 | 1,05 |
Из предложенного списка выберите два утверждения, соответствующих экспериментальным наблюдениям. Укажите их номера.
- При уменьшении длины проводника его электрическое сопротивление увеличивается.
- При увеличении толщины проводника его электрическое сопротивление уменьшается.
- Электрическое сопротивление проводника уменьшается при увеличении длины проводника.
- Электрическое сопротивление проводника зависит от материала, из которого изготовлен проводник.
- Удельное электрическое сопротивление алюминия больше, чем железа.
Решение
Из теории о постоянном токе $R=ρ·{l}/{S}$, тогда при увеличении толщины проводника, его электрическое сопротивление уменьшится, а электрическое сопротивление проводника зависит от материала, из которого изготовлен проводник.
Задача 14
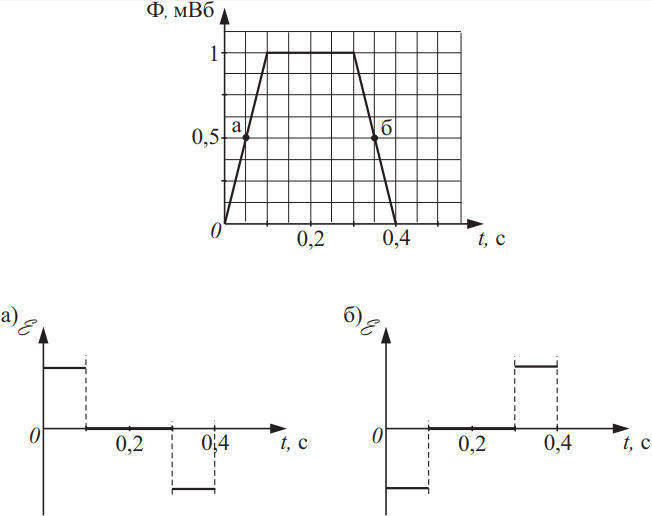
Магнитный поток, пронизывающий катушку, изменяется со временем, как показано на рисунке. Выберите все верные утверждения.
- Изменение ЭДС индукции, наводимой в катушке, верно изображено на рисунке а).
- ЭДС в точке а больше ЭДС в точке б.
- ЭДС определить невозможно, так как всё время ЭДС меняется.
- Изменение ЭДС индукции, наводимой в катушке, верно изображено на рисунке б).
- Модули ЭДС в точках а и б равны.
Решение
Согласно закону электромагнитной индукции: $ε_i=-{∆Ф}/{∆t}$, то изменение ЭДС индукции, проводимой в катушке, верно изображено на рисунке б. Модули ЭДС в точках а и б равны, так как скорость изменения магнитного потока одинакова.
Задача 15
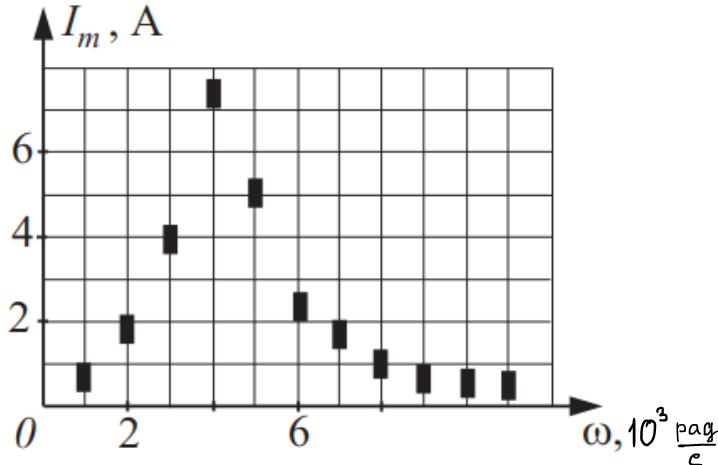
При исследовании зависимости амплитуды колебания тока в колебательном контуре от частоты внешнего переменного напряжения были получены следующие экспериментальные точки. Выберите два утверждения, соответствующих результатам этого опыта. Индуктивность катушки равна L = 25 мГн.
- В процессе опыта происходила диссипация механической энергии.
- Собственная циклическая частота колебаний контура примерно равна ω0 = 4 $ ·10^{3}$ рад/с.
- Электроёмкость конденсатора примерно равна 2,5 мкФ.
- Активное сопротивление контура примерно равно 2,5 Ом.
- В контуре при частоте внешнего напряжения ν = 4 · 103 с−1 происходит резонанс.
Решение
Из проведенного опыта очевидно, что собственная циклическая частота $ω_0=4$рад/с, т.к. именно при этой частоте на графике наблюдается резонансный пик (I=max). Собственная циклическая частота колебательного контура $ω_0={1}/{√{LC}}$, определим $С=2.5·10^{-6}Ф$(3).
Задача 16
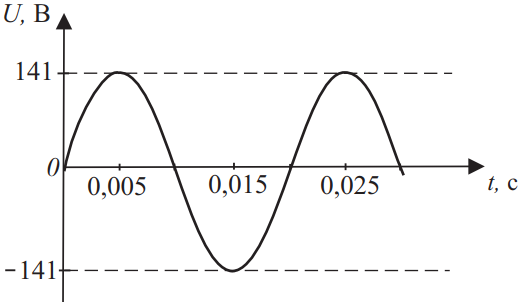
На рисунке показано, как менялось напряжение с течением времени. Из предложенного списка выберите два утверждения, соответствующих графику.
- Частота переменного тока 100 Гц.
- Частота переменного тока 50 Гц.
- Действующее значение напряжения 100 В.
- Действующее значение напряжения 141 В.
- Действующее значение напряжения 198,8 В.
Решение
2) Частота преломленного тока $v=50$Гц.
3) Из графика видно, что амплитудное значение напряжения $U_m=141B$, тогда действующее значение напряжения $U={U_m}/{√2}={141}/{1.41}=100B$.
Задача 17
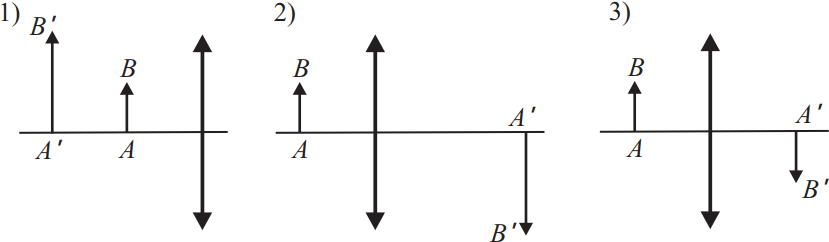
Ученик проводил опыты с собирающими линзами, изготовленными из одинакового сорта стекла. Условия проведения опытов показаны на рисунке. AB — предмет, A′ B′ — его изображение. Выберите из предложенного списка два утверждения, соответствующих результатам проведённых экспериментальных наблюдений.
- Наибольшее фокусное расстояние имеет линза 2.
- Наименьшее фокусное расстояние имеет линза 3.
- По отношению к линзе 3 предмет располагается в двойном фокусе.
- Собирающие линзы дают только действительные изображения.
- Собирающие линзы дают только увеличенные изображения.
Решение
Из основ оптики мы знаем, что для собирающей линзы с наименьшим фокусным расстоянием, изображение будет ближе к линзе(2). А расстояние 2 фокуса в том случае, если высота предмета и изображения одинакова(3).
Задача 18
В идеальном колебательном контуре происходят свободные электромагнитные колебания. В таблице показано, как изменялся заряд одной из обкладок конденсатора в колебательном контуре с течением времени.
| t, 10−6 c | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| q, 10−9 мкА | 2 | 1,42 | 0 | −1,42 | −2 | −1,42 | 0 | 1,42 | 2 | 1,42 |
Выберите все верные утверждения о процессе, происходящем в контуре.
- Период колебаний равен 8 мкс.
- В момент времени 8 мкс энергия конденсатора минимальна.
- В момент времени 6 мкс сила тока в контуре максимальна.
- В момент 2 мкс сила тока в контуре равна 0.
- Частота колебаний равна 25 кГц.
Решение
1) Период колебаний $8·10^{-6}$ c, верно, т.к. данные для заряда начинают повторяться через $8·10^{-6}$ c.
3) В момент $t=2·10^{-6}$. Сила тока в контуре максимальная, верно, т.к. заряд конденсатора минимален.
Задача 19

На рисунке изображены главная оптическая ось линзы, точка A и её изображение точка A′ . Какая линза использовалась и какое изображение при этом получилось? Выберите из предложенного списка два утверждения, соответствующих результатам опыта.
- Линза рассеивающая, изображение мнимое, прямое, уменьшенное.
- Линза рассеивающая, изображение мнимое, обратное, увеличенное.
- Линза собирающая, изображение действительное, обратное, уменьшенное.
- Линза собирающая, изображение действительное, обратное, увеличенное.
- Линза собирающая, т.к. по условию изображение и источник расположены по разные стороны от главной оптической оси.
Решение
Исходя из основ оптики можем сделать очевидный вывод: линза собирающая, изображение действительное, обратное, уменьшенное, т.к. условие изображения и источник расположены по рзаные стороны от главной оптической оси.
Задача 20
В квартире горят три лампочки мощностью 45 Вт, 75 Вт и 110 Вт. Напряжение и время горения одинаковые. Выберите два верных утверждения. (Учтите, что электропроводка в квартире устроена так, что электроприборы в подключаются параллельно)
- Наибольшее количество теплоты выделяет лампочка мощностью 45 Вт.
- Наибольшее количество теплоты выделяет лампочка мощностью 110 Вт.
- Каждая лампочка выделяет одинаковое количество теплоты, так как время горения и напряжение одинаковое.
- Электрическое сопротивление лампочки мощностью 110 Вт наибольшее.
- Электрическое сопротивление лампочки мощностью 45 Вт больше, чем у других ламп.
Решение
2) Наибольшее количество теплоты выделяет лампочка мощностью $p=110$Вт, т.к. $P={Q}/{t}⇒Q=P·t$, т.к. время одинаково, то наибольшее количество теплоты выделяет лампочка с большей мощностью.
5) Поскольку мощность $P=J·U={U}/{R}·U={U^2}/{R}$, то отсюда имеем, что $R={U^2}/{P}$, значит, чем меньше мощность лампочки, тем больше сопротивление при $U=const$.
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

