Задание 13. Электромагнитные колебания и волны. Оптика. ЕГЭ 2026 по физике
Средний процент выполнения: 78.7%
Ответом к заданию 13 по физике может быть целое число или конечная десятичная дробь.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
В опыте по измерению ЭДС индукции за 4 секунды магнитное поле увеличивают с 0 до 8 Тл. Во сколько раз увеличится ЭДС индукции, если увеличивать магнитное поле с 0 до 16 Тл всего за 2 секунды?
Решение
По скольку ЭДС индукции прямо пропорционально изменению потока (который увеличился в 2 раза) , и обратно пропорционально времени измерения ( которое уменьшилось в 2 раза), значит ЭДС индукции увеличится в 4 раза.
Задача 2
Заряд на пластинах конденсатора колебательного контура изменяется с течением времени по закону q = 10−6 · cos(104π · t). Найдите период колебания заряда. Ответ выразите в (·10−4 c).
Решение
Дано:
$q=10^{-6}·cos(10^4πt)$
$T-?$
Решение:
Из уравнения колебаний заряда видно, что циклическая частота $ω=10^4π$ (всё, что стоит перед t в аргументе косинуса).
Тогда период: $T={2π}/{ω}={2π}/{10^4π}=2·10^{-4}$c
Задача 3
Пучок параллельных лучей падает под углом 50◦ к горизонтальной зеркальной поверхности. Под каким углом к плоскости следует расположить второе плоское зеркало, чтобы после отражения от него пучок шёл вертикально вверх? Ответ выразите в (◦). В ответе укажите тупой угол
Решение
Дано:
$α=50°$
$θ-?$
Решение:
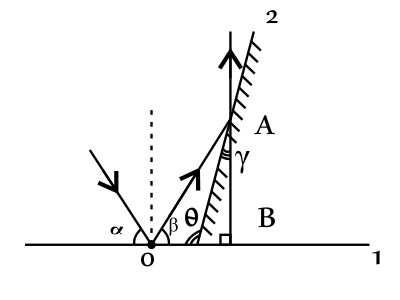
По закону отражения света $∠α=∠β=50°$(1). Из $∆OAB$ видно, что $∠ABO=90°, ∠AOB=∠B=50°$, значит, $∠OAB=180°-∠ABO-∠B=180°-90°-50°=40°$(2). Зеркало 2 делит $∠OAB$ пополам, значит, угол $γ={∠AOB}/{2}={40°}/{2}=20°$(3). Из $∆ABC$ имеем $∠ACB=180°-∠ABC-∠γ=180°-90°-20°=180°-110°=70°$(4). Из рисунка видно, что $∠θ$ и $∠ACB$ смежные углы, тогда имеем: $∠θ=180°-∠ACB=180°-70°=110°$.
Задача 4
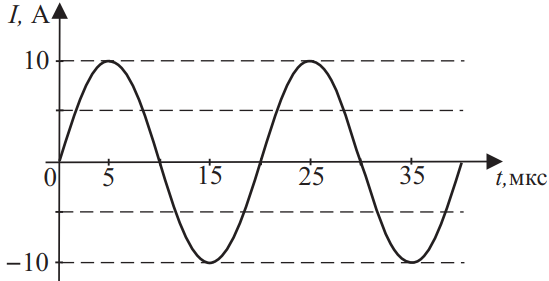
На рисунке приведён график гармонических колебаний тока в колебательном контуре. Если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 16 раз меньше, то каков будет период колебаний? Ответ выразите в (мкс).
Решение
1) По графику определим $T$ период гармонических колебаний, он равен 20мкс. По формуле Томсона $T=2π√{LC}$ определим, что при уменьшении емкости в 16 раз, период колебаний уменьшается в 4 раза $T_г={T_1}/{4}={20}/{4}=5$мкс.
Задача 5
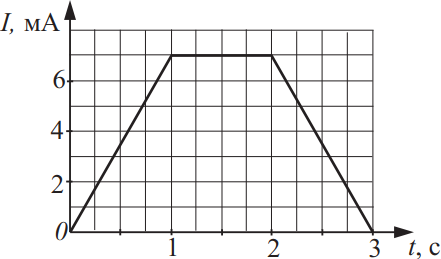
На рисунке приведена зависимость силы тока от времени в катушке с индуктивностью 0,4 Гн. Какова энергия магнитного поля, создаваемого током в катушке в момент времени 1,5 с? Ответ выразите в (мкДж).
Решение
Дано:
$L=0.4Гн$
$t=1.5c$
$J=7·10^{-3}А$
$W_м-?$
Решение:
Энергия магнитного поля, создаваемого током в катушке, определяется выражением: $W_м={LJ^2}/{2}$(1)
Из рисунка видно, что в момент времени $t=1.5c$ сила тока в катушке равна $J=7мА=7·10^{-3}А$
Подставим числовые значения в (2): $W_м={0.4·49·10^{-6}}/{2}=9.8·10^{-6}=9.8$мкДж
Задача 6
Человек приближается к зеркалу со скоростью 1 м/с. Насколько сокращается расстояние между ним и его изображением за 3 с? В ответе запишите на сколько (м).
Решение
Дано:
$t=3$c
$υ=1$м/с
$∆x-?$
Решение:
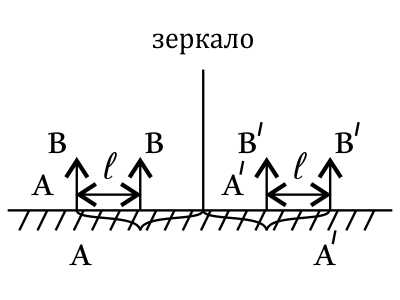
За 3 секунды человек приблизится к зеркалу на расстояние: $lS=υ·t=1·3=3$м. Значит, и изображение человека $A'B'$ так же приблизится к зеркалу на расстояние $l$, тогда расстояние между человеком $AB$ и его изображением $A'B'$ сокращается на $∆x=2l=2·3=6$м.
Задача 7
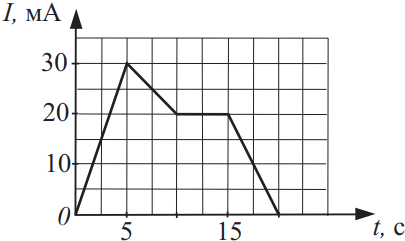
На рисунке приведён график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 10 до 15 с. Ответ выразить в (мкB).
Решение
Дано:
$h=1$мГн
$t_1=10c$
$t_2=15c$
$|ε_i|-?$
Решение:
Воспользуемся формулой для определения ЭДС самоиндукции $|ε_i|={L|∆I|}/{∆t}={1·10^{-3}(20-20)·10^3}/{5}=0B$.
Задача 8
Расстояние от карандаша до его изображения в плоском зеркале было равно 90 см. Карандаш приблизили к зеркалу на 10 см. Каково стало расстояние между карандашом и его изображением? Ответ выразите в (см).
Решение
При приближении карандаша на 10 см, приблизится изображение тоже на 10. Тогда, 90-10-10=70см.
Задача 9
В колебательном контуре, индуктивность катушки которого равна 0,4 Гн, происходят собственные электромагнитные колебания. Определите электроёмкость конденсатора в этом контуре, если зависимость напряжения на конденсаторе от времени для этого колебательного контура имеет вид U = U0 cos(500t). Все величины в формуле выражены в единицах СИ. Ответ выразите в (мкФ).
Решение
Дано:
$L=0.4$Гн
$U=U_0cos(500t)$
$C-?$
Решение:
Из уравнения $ω=500$.
$ω={1}/{√{LC}}$, тогда $C={1}/{Lω^2}={1}/{0.4·500^2}=10$мкФ.
Задача 10
В таблице показано, как изменялся заряд конденсатора в колебательном контуре с течением времени.
| t, 10−6, c | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| q, 10−6, Кл | 0 | 2,13 | 3 | 2,13 | 0 | −2,13 | −3 | −2,13 | 0 | 2,13 |
Вычислите ёмкость конденсатора в контуре, если индуктивность катушки равна 65 мГн. Ответ выразите в (пФ) и округлите до целых.
Решение
Дано:
$L=65·10^{-3}$Гн
$T=16·10^{-6}$с
$π=3.14$
$С-?$
Решение:
Из таблицы видно, что период колебаний заряда конденсатора в колебательном контуре $T=16·10^{-6}c$. Запишем формулу Томсона: $T=2π√{LC}$(1), откуда выразим емкость конденсатора С: ${T}/{2π}=√{LC}⇒{T^2}/{4π^2}=LC⇒C={T^2}/{4π^2L}$(2). Подставим числовые значения в (2): $C={256·10^{-12}}/{39.4384·65·10^{-3}}=0.1·10^{-9}=100·10^{-12}=100$пФ.
Задача 11
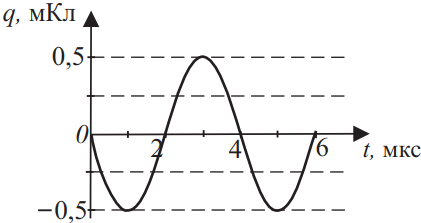
На рисунке изображён график зависимости заряда конденсатора от времени при свободных колебаниях в колебательном контуре. Чему станет равным период колебаний заряда конденсатора, если индуктивность катушки контура уменьшить в 4 раза? Ответ выразите в (мкс).
Решение
Дано:
$q_m=0.5·10^{-3}Кл$
$L_1=L; C_1=C_2=C$
$L_2={L}/{4}$
$T_1=4·10^{-6}c$
$T_2-?$
Решение:
Период колебаний в колебательном контуре рассчитывается по формуле Томсона $T=2π√{LC}$(1), где С - емкость конденсатора. Тогда имеем: $T_1=2π√{L_1C_1}=2π√{LC}$(2); $T_2=2π√{L_2C_2}=2π√{{L}/{4}·C}={2π}/{2}√{LC}=π√{LC}$(3)
Разделим (3) на (2), получим: ${T_2}/{T_1}={π√{LC}}/{2π√{LC}}={1}/{2}$ или $T_2={T_1}/{2}={4·10^{-6}}/{2}=2·10^{-6}c=2мкс$
Задача 12
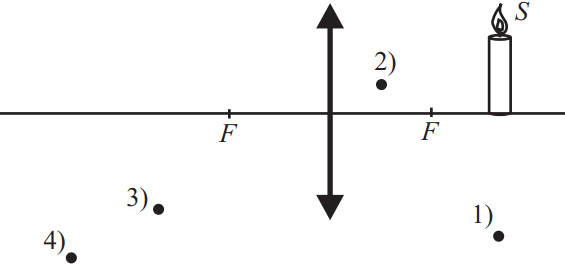
В какой точке будет находиться изображение пламени свечи (обозначено буквой S) в линзе, изображённой на рисунке? В ответе запишите номер точки.
Решение
1) Учитывая, что данная линза собирающая и находится за фокусом, ее изображение будет увеличенным, соответствует точке 4.
Задача 13
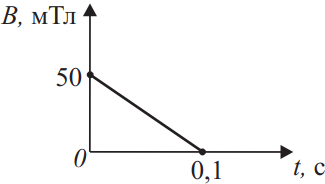
Внутри проволочного витка радиусом 10 см магнитная индукция В меняется со временем так, как показано на графике зависимости индукции от времени. Определите ЭДС индукции в этом витке. Виток расположен в плоскости, перпендикулярной линиям магнитной индукции. Ответ выразите в (мВ) и округлите до десятых.
Решение
Дано:
$R=0.1м$
$∆t=0.1с$
$∆B=-50·10^{-3}Тл$
$π=3.14$
$ε_i-?$
Решение:
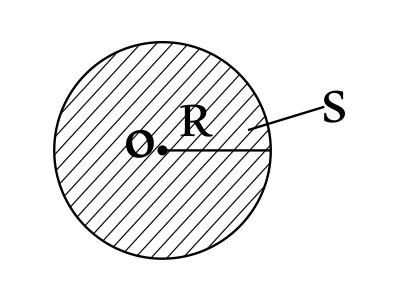
По закону электромагнитной индукции имеем: $ε_i=-{∆Ф}/{∆t}$(1), где $∆Ф=∆B·S$(2), где $S$ - площадь витка $S=πR^2$(3), тогда подставим (2) и (3) в (1) получим: $ε_i=-{∆B·πR^2}/{∆t}=-{(-50·10^{-3})·3.14·10^{-2}}/{0.1}=15.7·10^{-3}=15.7мВ$
Задача 14
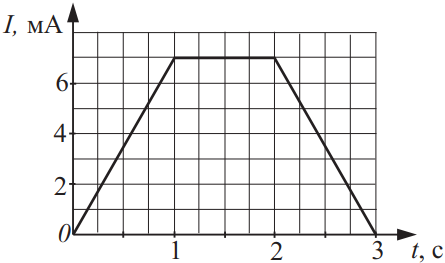
На рисунке приведена зависимость силы тока в катушке от времени. Какова индуктивность катушки, если энергия магнитного поля, создаваемого током в катушке в момент времени 1,8 с, равна 14,7 мкДж? Ответ выразите в (Гн).
Решение
Дано:
$t=1.8c$
$W_м=14.7·10^{-6}$Дж
$L-?$
Решение:
Энергия магнитного поля определяется выражением: $W_м={LJ^2}/{2}$(1)
Из рисунка видно, что в момент времени $t=1.8c$ сила тока в катушке равна $J=7мА=7·10^{-3}А$
Из (1) выразим индуктивность $L: L={2W_м}/{J^2}$
Подставим числовые значения в (2): $L={2·14.7·10^{-6}}/{49·10^{-6}}=0.6$Гн
Задача 15
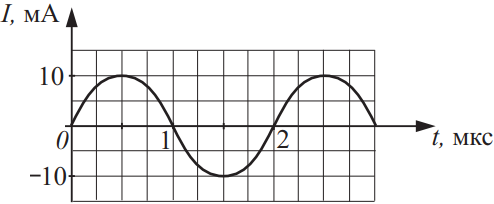
На рисунке приведена зависимость силы тока в колебательном контуре от времени. Какова амплитуда колебания заряда на обкладках конденсатора? Ответ выразите в (нКл) и округлите до целых.
Решение
Дано:
$J_m=10^{-2}A$
$T=2·10^{-6}c$
$π=3.14$
$q_m-?$
Решение:
Энергия магнитного поля катушки индуктивности равна энергии электрического поля конденсатора: $W_м=W_э$(1) и ${LJ_m^2}/{2}={q_m^2}/{2C}⇒q_m=√{LC}·J_m$(2), где $J_m$ - амплитуда тока, $q_m$ - амплитуда колебания заряда.
Из графика видно, что $J_m=10мА=10А$, и период колебаний колебательного контура $T=2мкс=2·10^{-6}с$. Учтем, что по формуле Томсона: $T=2π√{LC}⇒√{LC}={T}/{2π}$(3). Подставим (3) в выражение (2): $q_m=√{LC}·J_m={T·J_m}/{2π}={2·10^{-6}·10^{-2}}/{6.28}=0.318·10^{-8}=3.18·10^{-9}=3нКл$
Задача 16
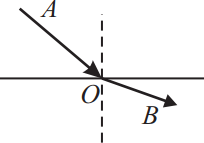
Световой луч переходит из одной среды в другую, как показано на рисунке. Можно ли, увеличивая угол падения, наблюдать явление полного внутреннего отражения? В ответе запишите одно из слов: да, нет
Решение
Явление полного отражения напрямую зависит от показателей преломления сред $n_2 > n_1$, следовательно, можно наблюдать.
Задача 17
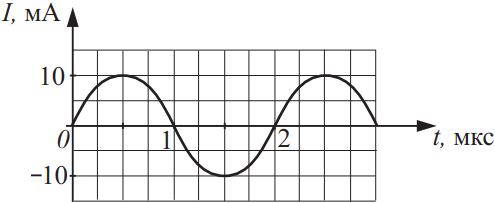
На рисунке приведена зависимость силы тока в колебательном контуре от времени. Какова индуктивность катушки, если ёмкость конденсатора равна 1 пФ? Ответ округлите до десятых. Ответ выразите в (Гн).
Решение
Дано:
$С=10^{-12}ф$
$T=2·10^{-6}c$
$π=3.14$
$L-?$
Решение:
Из графика видно, что период колебаний силы тока равен $T=2мкс=2·10^{-6}c$. Запишем формулу Томсона: $T=2π√{LC}$, откуда $T^2=4π^2LC⇒L={T^2}/{4π^2C}$. Подставим числовые значения: $L={4·10^{-12}}/{4·9.8596·10^{-12}}=0.101Гн≈0.1Гн$
Задача 18
В колебательном контуре с индуктивностью 0,4 Гн и ёмкостью 20 мкФ амплитудное значение силы тока равно 0,1 А. Каким будет напряжение на конденсаторе в момент, когда энергия электрического и магнитного полей будут равны? Колебания считать незатухающими. Ответ выразите в (В).
Решение
Дано:
$С=20·10^{-6}ф$
$L=0.4$Гн
$J_m=0.1$А
$W_м=W_э$
$U-?$
Решение:
По условию задачи колебания в колебательном контуре являются не затухающими, значит, колебательный контур идеальный, т.е. в нем нет потерь энергии и выполняется закон сохранения энергии. Вся энергия в контуре равна максимальной магнитной энергии: $W=W_{м,max}={LJ_m^2}/{2}={0.4·10^{-2}}/{2}=2·10^{-3}$Дж. Значит, в момент времени, когда $W_м=W_э={W}/{2}$, т.е. $W_э={2·10^{-3}}/{2}=10^{-3}$Дж. Учитывая, что электрическая энергия конденсатора в этот момент $W_э={CU^2}/{2}$, выразим напряжение $U$: $2W_э=CU^2$, откуда $U=√{{2W_э}/{C}}=√{{2·10^{-3}}/{20·10^{-6}}}=√{100}B=10B$.
Задача 19
Каков абсолютный показатель преломления стекла, если скорость света в стекле 200 Мм/с?
Решение
Дано:
$υ=2·10^8{м}/{с}$
$с=3·10^8{м}/{с}$
$n-?$
Решение:
Показатель преломления отражает во сколько скорость света в веществе меньше, чем скорость света в вакууме: $n={c}/{υ}$, где $c$ - скорость света в вакууме. $n={3·10^8}/{2·10^8}={3}/{2}=1.5$
Задача 20
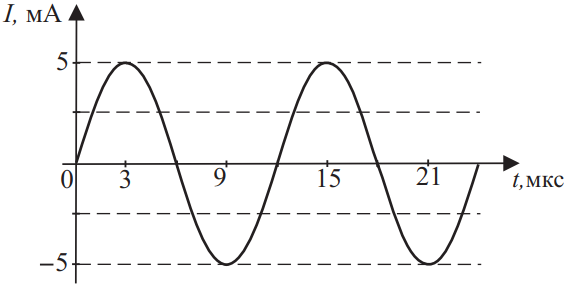
На рисунке приведён график зависимости силы тока в колебательном контуре при свободных колебаниях от времени. Чему будет равен период колебаний контура, если катушку индуктивности в этом контуре заменить на другую с индуктивностью в 9 раз меньшей? Ответ выразите в (мкс).
Решение
1) Исходя из графика, начальный период $T_0=12$мкс.
2) По условию $L=1/9L_0$
3) По формуле Томсона
$T_0=2π√{L_0C}$
$T=2π√{LC}=2π√{{L_0}/9C}=2π{1}/{3}√{{L_0}C}$
$T={T_0}/{3}={12}/{3}=4$мкс (уменьшение периода в 3 раза)
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

