Задание 12. Магнитное поле. Электромагнитная индукция. ЕГЭ 2026 по физике
Средний процент выполнения: 71.9%
Ответом к заданию 12 по физике может быть цифра (число) или слово.
Алгоритм решения задания 12:
- Определи, относится ли описанный процесс к магнитному полю или к явлениям электромагнитной индукции.
- Выдели физические величины, характеризующие процесс: магнитную индукцию, силу, магнитный поток.
- Установи, какие изменения происходят в системе: движение проводника, изменение магнитного поля или потока.
- Соотнеси ситуацию с соответствующим законом магнитных или индукционных явлений.
- Запиши применимый закон в общем виде через физические величины.
- Используй закон для описания направления, величины или характера явления.
- Проверь, что результат согласуется с физическим смыслом магнитных и индукционных процессов.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Плоский воздушный конденсатор, площадь каждой пластины которого 50 см2, а расстояние между пластинами 5 см, подключён к источнику напряжения с ЭДС E = 2,5 кВ и с пренебрежимо малым внутренним сопротивлением. Чему равна напряжённость электростатического поля в этом конденсаторе? Ответ выразите в (В/см).
Решение
Дано:
$S=50см^2$
$d=5см$
$ε=2.5·10^3B$
$E-?$
Решение:
Из формулы определения напряжения $U=Ed$ выражаем: $E={U}/{d}$
Т.к. внутренне сопротивление источника пренебрежимо мало, $U=ε$
Тогда: $E=ε/d={2.5·10^3В}/{5см}=500В/{см}$ .
Задача 2
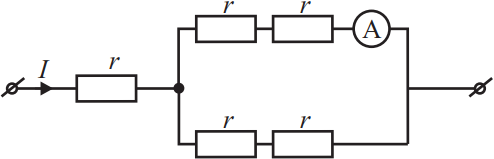
Через участок цепи течёт постоянный ток I = 10 А. Чему равна сила тока, которую показывает амперметр? Сопротивлением амперметра пренебречь. Ответ выразите в (А).
Решение
Дано:
$J=10A$
$r$
$J_A-?$
Решение:
Согласно первого правила Кирхюфа сумма токов в узле равна нулю: $J=J_1+J_2$(1). Учитывая, то обстоятельство, что сопротивление ветвей одинаковое и равно $2r$, а так же, что падение напряжения в них одинакова, так как они соединены парллельно друг другу, то по закону Ома имеем: $J_1=J_2={U_1}/{2r}={U_2}/{2r}={J}/{2}={10}/{2}=5A; J_A=J_1=5A$
Задача 3
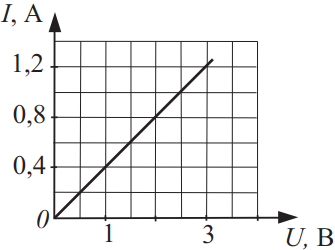
Каково сопротивление проводника, вольт-амперная характеристика которого изображена на рисунке? Ответ выразите в (Ом).
Решение
Дано:
$U=1B$
$J=0.4A$
$R-?$
Решение:
Запишем закон Ома: $J={U}/{R}$(1), откуда $R={U}/{J}$(2). На вольт-амперной характеристике возьмем любую точку, например, точку с координатами $U=1B, J=0.4A$. Подставим числа в (2): $R={1}/{0.4}=2.5$Ом.
Задача 4
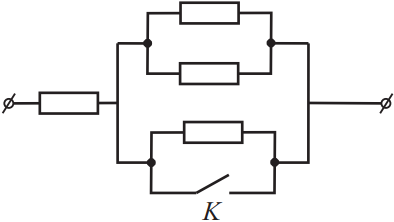
Каждый из резисторов на участке цепи, схема которого изображена на рисунке, имеет сопротивление 120 Ом. Каким будет сопротивление участка цепи, если ключ K замкнуть? Ответ выразите в (Ом).
Решение
$R=120$Ом. При замыкании цепи ключа К электрический ток протекает по пути с нулевым сопротивлением, то есть через ключ, в обход всех резисторов в параллельном соединении. В этом случае участок упростится и лишь через один резистор (самый левый) будет протекать ток, поэтому сопротивление участка будет равно сопротивлению одного резистора: $R_{общ}=R=120$
Задача 5
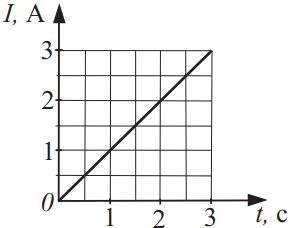
Как увеличится мощность, выделяющаяся в проводнике за вторую секунду, если сила тока, протекающего в этом проводнике с сопротивлением 15 Ом, меняется со временем так, как показано на рисунке? В ответе запишите во(в) сколько раз(-а).
Решение
Дано:
$t_2-?$
$R=150$м
${P_2}/{P_1}-?$
Решение:
1) ${P_2}/{P_1}={I_2^2·R}/{I_1^2·R}={2^2·R}/{1^2·R}=4$.
Отношение мощности за 1 и 2 секунды.
Задача 6
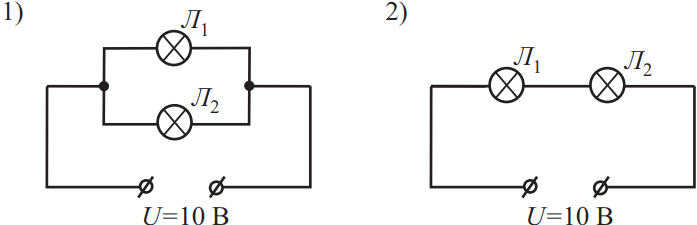
Лампочка Л1 имеет сопротивление R, а лампочка Л2 имеет сопротивление 2R. Эти лампочки подключают двумя разными способами, изображёнными на рисунках 1 и 2. Во сколько раз отличаются мощности, выделяющиеся в лампочке Л1, в первом и во втором случае?
Решение
Дано:
$λ_1∼R_1=R$
$λ_2∼R_2=2R$
$R$ - сопротивление
$U=10B$
${P_1}/{P_2}-?$
Решение:
1) Формула для нахождения мощности $P=I·U={U^2}/{R}=I^2·R$.
2) В случае параллельного соединения на каждом участке цепи одинаковые напряжения: $U_1=U_2=U$. При последовательном токе $I_1=I_2=I; I={U}/{R_1+R_2}$
Тогда ${P_1}/{P_2}={{U^2}/{R_1}}/{{I^2}·R_1}={{U^2}/{R_1}}/{({U}/{R_1+R_2})^2·R_1}={(R_1+R_2)^2}/{R_1^2}={(R_1+R_2)^2}/{R^2}=9$
Задача 7
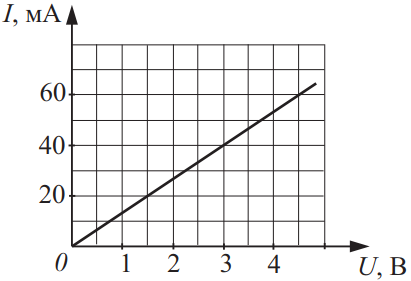
На рисунке изображён график зависимости силы тока от напряжения на некотором участке цепи. Чему равно сопротивление этого участка? Ответ выразите в (Ом).
Решение
Решение:
Выберем произвольную точку на графике, используем её координаты для закона Ома для участка цепи: $R={U}/{I}={3}/{40·10^{-3}}=75$Ом.
Задача 8
Два одинаковых проводящих шарика малых размеров расположены в воздухе так, что расстояние между их центрами равно 60 см, а их заряды равны 4 · 10−7 Кл и 0,8 · 10−7 Кл. Шарики приводят в соприкосновение, а затем удаляют на прежнее расстояние. Определите силу их взаимодействия после соприкосновения. Ответ округлите до десятых. Ответ выразите в (мН).
Решение
Дано:
$r=0.6$м
$q_1=4·10^{-7}$Кл
$q_2=0.8·10^{-7}$Кл
$F_2-?$
Решение:
Сила взаимодействия двух заряженных шариков, согласно закону Кулона равна: $F={k·q_1·q_2}/{r^2}$(1), где $k=9·10^9{Н·м^2}/{Кл^2}$- коэффициент пропорциональности.
Согласно закону сохранения электрического заряда, после соприкосновения, заряды шариков станут одинаковыми, т.к. размеры шариков одинаковы: $q_1+q_2=q'+q'=2q'$, откуда $q'={q_1+q_2}/{2}={4·10^{-7}+0.8·10^{-7}}/{2}=2.4·10^{-7}$Кл(2).
Найдем силу их взаимодействия $F_2$ после соприкосновения: $F_2={k·q'·q'}/{r^2}={kq'_2}/{r^2}={9·10^9·5.76·10^{-14}}/{0.36}=144·10^{-5}=1.4$мН.
Задача 9
Между двумя точечными заряженными телами сила электрического взаимодействия равна 30 мН. Если заряд одного тела увеличить в 2 раза, а заряд другого тела уменьшить в 3 раза и расстояние между телами увеличить в 2 раза, то какова будет сила взаимодействия между телами? Ответ выразите в (мН).
Решение
Дано:
$F_1=30·10^{-3}H$
$q_1=q$
$q_2=q$
$q′_1=2q$
$q′_2={q}/{3}$
$r_1=r$
$r_2=2r$
$F_2-?$
Решение:
Запишем закон Кулона: $F=k{q_1q_2}/{r^2}$(1), где $k=9·10^9{H·м^2}/{Кл^2}$ - коэффициент пропорциональности. Тогда сила $F_1$ равна: $F_1=k{q_1q_2}/{r^2}={kqq}/{r^2}$(2), сила $F_2$ равна: $F_2=k{q′_1q′_2}/{r^2}={k·2q·{q}/{3}}/{(2r)^2}={k·2q·q}/{12r^2}$(3). Разделим выражение (3) на (2) почленно, имеем: ${F_2}/{F_1}={2kq^2}/{12r^2}:{kq^2}/{r^2}={kq^2}/{6r^2}·{r^2}/{kq^2}={1}/{6}$ или $F_2={F_1}/{6}={30·10^{-3}}/{6}=5·10^{-3}=5$мН.
Задача 10
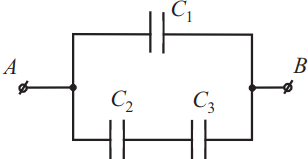
Ёмкость батареи конденсаторов равна 5,8 мкФ. Какова ёмкость первого конденсатора C1, если C2 = 1 мкФ, C3 = 4 мкФ? Ответ выразите в (мкФ).
Решение
Дано:
$С_2=10^{-6}$ф
$С_3=4·10^{-6}$ф
$С=5.8·10^{-6}$ф
$С_1-?$
Решение:
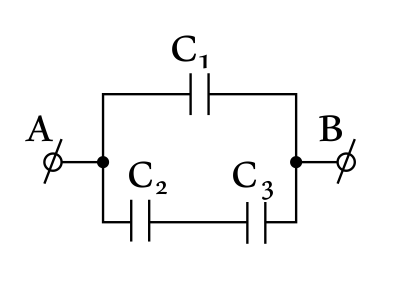
Конденсаторы $С_2$ и $С_3$ соединены последовательно, тогда их общая емкость $С_{23}$ определится из выражения: ${1}/{С_{23}}={1}/{С_2}+{1}/{С_3}={С_2+С_3}/{С_2С_3}$ или $С_{23}={С_2С_3}/{С_2+С_3}$(1).
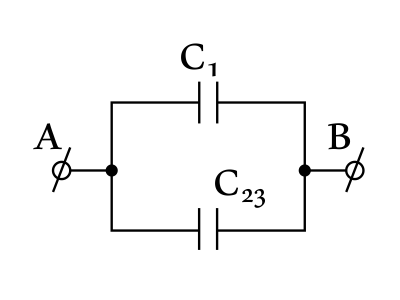
Эквивалентная схема изображена на рисунке. Из нее видно, что электроемкости $С_2$ и $С_{23}$ соединены параллельно, значит, их общую емкость можно найти из выражения: $C=C_1+C_{23}$(2), откуда $C_1=C-C_{23}=5.8·10^{-6}-{10^{-6}·4·10^{-6}}/{5·10^{-6}}=5.8·10^{-6}-0.8·10^{-6}=5·10^{-6}=5$мкФ.
Задача 11
Какой заряд нужно сообщить двум параллельно соединённым конденсаторам, чтобы зарядить их до разности потенциалов 12 кВ, если известно, что электроёмкости конденсаторов равны 2 нФ и 3 нФ? Ответ выразите в (мкКл).
Решение
Дано:
$U=12·10^3$В
$C_1=2·10^{-9}$ф
$C_2=3·10^{-9}$ф
$q-?$
Решение:
Известно, что при параллельном соединении $C_1+C_2=C=5·10^{-9}$ф.
А заряд $q=C·U=5·10^{-9}·12·10^3=60$мкКл.
Задача 12
По проводнику из никелина сечением 4 мм2 протекает ток 10 мА при напряжении на концах проводника 12 мВ. Найдите длину проводника. Удельное электрическое сопротивление никелина 0,4 Ом·мм2 /м. Ответ выразите в (м).
Решение
Дано:
$l-?$
$S=4мм^2$
$I=10^{-2}$A
$U=12·10^{-3}B$
$ρ_{уд}=0.4({Ом⋅мм^2}/м)$
Решение:
По закону Ома $R={U}/{I}$ выразим:.
$R=ρ_{уд}·{l}/{S}={U}/{I}⇒l={U·S}/{I·ρ_{уд}}={12·10^{-3}(В)·4(мм^2)}/{10^{-2}(А)·0.4({Ом⋅мм^2}/м)}=12$м
Задача 13
Два одинаковых плоских воздушных конденсатора соединены последовательно и подключены к источнику с постоянной ЭДС. Как увеличится модуль напряжённости поля во втором конденсаторе при заполнении пространства между обкладками одного из конденсаторов диэлектриком с диэлектрической проницаемостью ε = 2? В ответе запишите во(в) сколько раз(-а). Округлите до сотых.
Решение
Решение:
Модуль напряженности $∆E-?$ при $ε=2$.
$U_1=U_2={U}/{2}; U_1={q}/{c_1}; U_2={q}/{εc_1}={U}/{ε};U=U_1+U_2=U_2(1+ε)$.
Преобразуем и получим: $∆E={E'_2}/{E_2}={{U'_2}/{d}}/{{U_2}/{d}}={U'_2}/{U_2}={U}/{1+ε}·{2}/{U}={2}/{1+2}=0.67$.
Задача 14
Как нужно уменьшить расстояние между двумя точечными зарядами, чтобы сила их взаимодействия увеличилась в 16 раз? В ответе запишите во(в) сколько раз(-а).
Решение
По закону Кулона $F=K{|q_1|·|q_2|}/{r^2}$ очевидно, что если сила увеличится в 16 раз, расстояние уменьшить в 4 раза.
Задача 15
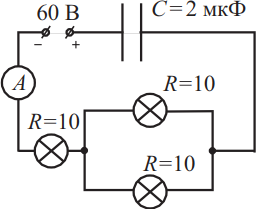
На рисунке изображена электрическая схема. Номиналы сопротивления ламп указаны в омах. Что показывает амперметр в момент времени, когда конденсатор полностью заряжен? Ответ выразите в (А).
Решение
В электрической схеме изображен источник постоянного тока, а конденсатор, включенный в цепь является разрывом цепи. Конденсатор может пропускать лишь переменный ток, а постоянный ток, он не пропускает, следовательно, амперметр будет показывать $J=0A$.
Задача 16
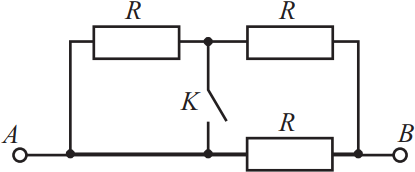
Чему равно сопротивление участка цепи AB, изображённого на рисунке при замкнутом ключе? Сопротивление каждого резистора 3 Ом. Ответ выразите в (Ом).
Решение
Дано:
$R=3$Ом
$R_{AB}-?$
Решение:
Перечертим рисунок в виде и обозначим резисторы $R_1, R_2,R_3$ для удобства пояснение: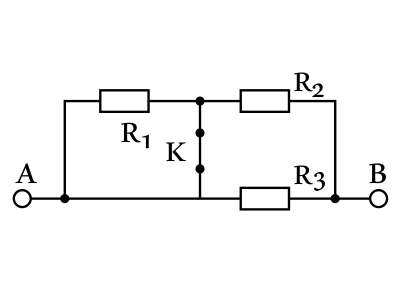
Из рисунка видно, что резистор $R_1$ закорочен, ток по нему не потечет (т.к. ток всегда течет по пути наименьшего сопротивления), поэтому $R_1$ можно исключить из схемы: 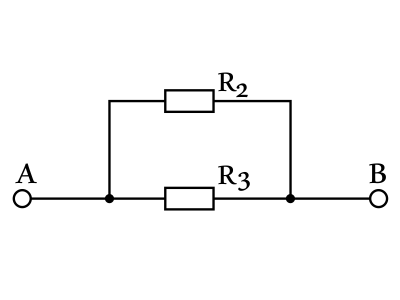 . Сопротивления $R_2$ и $R_3$ соединены параллельно, поэтому: ${1}/{R_{AB}}={1}/{R_1}+{1}/{R_2}={1}/{3}+{1}/{3}={2}/{3}$ или $R_{AB}={3Ом}/{2}=1.5Ом$
. Сопротивления $R_2$ и $R_3$ соединены параллельно, поэтому: ${1}/{R_{AB}}={1}/{R_1}+{1}/{R_2}={1}/{3}+{1}/{3}={2}/{3}$ или $R_{AB}={3Ом}/{2}=1.5Ом$
Задача 17
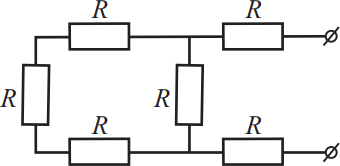
Общее сопротивление участка цепи, изображённого на рисунке, 22 Ом. Найдите сопротивление R каждого отдельного резистора. Ответ выразите в (Ом).
Решение
Дано:
$R_{общ}=22$Ом
$R_1-?$
Решение:
Определим по формуле, общее сопротивление цепи, путем последовательного и параллельного соединения.
$R_{общ}=2R+{3R^2}/{4R}=2R+{3}/{4}R=22⇒R={22}/{2.75}=8$Ом.
Задача 18
Электрическая лампа мощностью 60 Вт зимой в среднем горит 8 часов в сутки. Сколько электроэнергии в течение одного зимнего месяца потребит эта лампа? Считать, что в одном зимнем месяце в среднем 30 дней. Ответ выразить в (МДж).
Решение
Дано:
$P=60$Вт
$t=8$ч
$T=30υ$
$Q-?$
Решение:
$Q=P·t·T=60·8·3600·60=51.84$мДж.
Задача 19
Какова величина электрического заряда, создающего поле с напряжённостью 70 кВ/м в точке, удалённой на расстояние 1,5 см от него? Ответ выразите в (нКл).
Решение
Дано:
$E=70000{В}/{м}$
$r=0.015м=15·10^{-3}м$
$k=9·10^{9}{м}/{ф}$
$E-?$
Решение:
Напряженность поля точечного заряда определяется выражением: $E={kq}/{r^2}$(1), откуда $q={E·r^2}/{k}$(2).
Подставим числовые значения: $q={7·10^{4}·225·10^{-6}}/{9·10^{9}}=1.75·10^{-9}Кл$
Задача 20
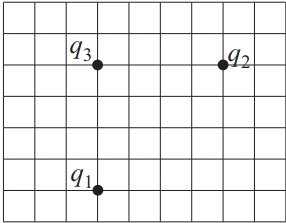
Три точечных заряда q1, q2 и q3 расположены, как показано на рисунке, при этом q1 = q0, q2 = 3q0, q3 = 2q0. Сила взаимодействия между зарядами q1 и q3 равна F13 = 4 Н. Определите равнодействующую сил, действующих на заряд q3. Ответ округлите до целых.
Решение
Дано:
$q_1=q_0$
$q_2=3q_0$
$q_3=2q_0$
$F_{13}=4H$
$R-?$
Решение:
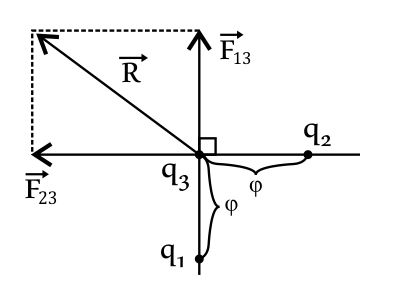
Заряды $q_1$ и $q_3$, $q_2$ и $q_3$ находятся на одинаковом расстоянии друг от друга. По закону Кулона имеем: $F_{13}=k{q_1q_3}/{r^2}={kq_0·2q_0}/{r^2}={2kq_0^2}/{r^2}$(1), тогда $F_{23}={kq_2q_3}/{r^2}={k3q_0·2q_0}/{r^2}={6kq_0^2}/{r^2}$(2).
Найдем силу $F_{23}$ для этого разделим (2) на (1): ${F_{23}}/{F_{13}}={6kq_0^2}/{r^2}:{2kq_0^2}/{r^2}={6kq_0^2}/{r^2}·{r^2}/{2kq_0^2}=3$ или $F_{23}=3F_{13}=3·4=12H$
Из рисунка видно, что равнодействующая $R↖{→}$ двух сил ${F_{13}}↖{→}$ и ${F_{23}}↖{→}$ по теореме Пифагора равна: $R=√{F_{13}^2+F_{23}^2}=√{(4)^2+(12)^2}=√{16+144}=√{160}H=12.649H≈13H$
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

