Задание 9. Задачи на квадратной решетке. ЕГЭ 2026 по математике (базовой)
Средний процент выполнения: 96.3%
Алгоритм решения задания 9:
Определите, какие геометрические фигуры и элементы описаны в условии задачи.
Установите, какие свойства, признаки или теоремы планиметрии применимы в данной ситуации.
Выразите искомые величины через известные, используя геометрические соотношения.
Выполните необходимые вычисления, соблюдая единицы измерения.
Оцените, соответствует ли полученный результат реальным размерам описанного объекта.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
На клетчатой бумаге с размером клетки $1× 1$ отмечены точки $A$, $B$ и $C$. Найдите квадрат расстояния от точки $A$ до прямой $BC$.
Решение
Найдём стороны $△ABC$.
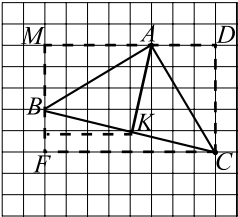
Из $△ABM : AB = √{AM^2 + MB^2} = √{25 + 9} = √34$;
Из $△ADC : AC = √{AD^2 + DC^2} = √{9 + 25} = √34$.
Из $△BF C : BC = √{BF^2 + FC^2} = √{4 + 64} = √{68} = 2√17$.
Итак, $△ABC$ — равнобедренный, значит высота $AK$ является и медианой. Точка $K$ делит $BC$ пополам, $BK = {BC}/{2}$.
$BK = √17$. Из $△ABK : AK^2 = AB^2 - BK^2 = 34 - 17 = 17. AK^2 = 17$.
Задача 2
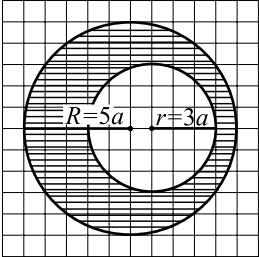
На клетчатой бумаге изображены два круга (см. рис. ). Площадь внутреннего круга равна $27$. Найдите площадь заштрихованной фигуры.
Решение
Площадь заштрихованной фигуры равна разности площадей кругов радиусов $R = 5a$ и $r = 3a$, где $a$ — длина стороны клетки, тогда $S = πR^2 - πr^2 = π · (5a)^2 - π · (3a)^2 = 25πa^2 - 9πa^2 = 16πa^2$; но по условию площадь малого круга равна $27$, то есть $9πa^2 = 27, πa^2 = 3$. Подставим $πa^2 = 3$ в $S = 16πa^2 = 16 · 3 = 48$.
Задача 3
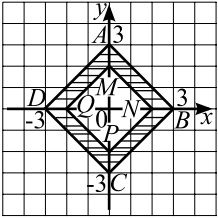
Найдите площадь заштрихованной фигуры на координатной плоскости с размером клетки $1$ см $×$ $1$ см (см. рис. ).
Решение
Четырёхугольники $ABCD$ и $A_1B_1C_1D_1$ — квадраты, так как: 1. $AB=BC=CD=DA$ и диагонали $BD$ и $AC$ взаимно перпендикулярны и равны (см. рис. ). 2. $A_1B_1=B_1C_1=C_1D_1=D_1A_1$ и диагонали $B_1D_1$ и $A_1C_1$ взаимно перпендикулярны и равны. Площадь заштрихованной фигуры равна разности площадей квадратов со сторонами $AB=√ {9+9}=√ {18}$ и $A_1B_1=√ {1+1}=√ {2}$. $S=S_{1}-S_2=AB^2-A_1B_1^2=(√ {18})^2-(√ {2})^2=18-2=16$.
Задача 4
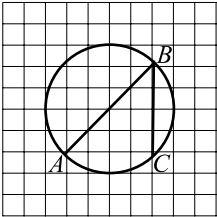
Найдите градусную меру дуги $AC$ окружности, на которую опирается угол $ABC$ (см. рис. ). Ответ дайте в градусах.
Решение
Из рисунка видно, что дуга $AC$ составляет ${1}/{4}$ дуги окружности. Вычислим ${1}/{4} · 360° = 90°$.
Задача 5
На клетчатой бумаге изображены два круга (см. рис. ). Площадь внутреннего круга равна $12$. Найдите площадь заштрихованной фигуры.
Решение
Площадь заштрихованной фигуры (см. рис. ) равна разности площадей кругов радиусов $R=5a$ и $r=2a$, где $a$ — длина стороны клетки, тогда $S=π R^2-π r^2=π⋅ (5a)^2-π⋅ (2a)^2=25π a^2-4π a^2=21π a^2$; но по условию площадь малого круга равна $12$, то есть $4π a^2=12$, $π a^2=3$. Подставим $π a^2=3$ в $S=21π a^2=21⋅ 3=63$.
Задача 6
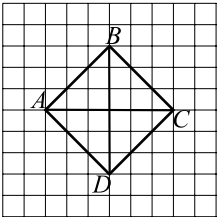
На клетчатой бумаге с размером клетки $1$ см $×$ $1$ см изображён квадрат (см. рис. ) Найдите радиус окружности, описанной около этого четырёхугольника.
Решение
$ABCD$ по условию квадрат, центр описанной окружности находится в точке пересечения диагоналей, то есть диагональ $AC$ является её диаметром, равным 6, значит радиус этой окружности равен 3.
Задача 7
На клетчатой бумаге с размером клетки $√ {13}$ см $×$ $√ {13}$ см изображён треугольник $ABC$ (см. рис. ). Найдите длину его высоты, опущенной на сторону $BC$.
Решение
Найдём стороны треугольника $ABC, AB = √{26} · √{13} = 13√2, AC = √{26} · √{13} = 13√2, BC = √{52} · √{13} = 2 · 13 = 26$. Получаем, что $△ABC$ — прямоугольный, так как $BC^2 = AB^2 + AC^2, △ABC$ — равнобедренный, $∠C AB = 90°$, тогда высота, опущенная на сторону $BC$ будет равна половине $BC$, то есть $13$.
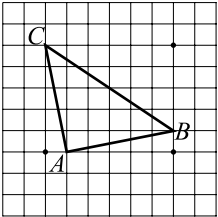
Задача 8
На клетчатой бумаге с размером клетки $√ {13}$ см $×$ $√ {13}$ см изображён треугольник $ABC$ (см. рис. ). Найдите длину его высоты, опущенной на сторону $BC$.
Решение
Найдём стороны треугольника $ABC, AB = √{26} · √{13} = 13√2, AC = √{26} · √{13} = 13√2, BC = √{52} · √{13} = 2 · 13 = 26$.
Получаем, что треугольник $ABC$ — прямоугольный, так как $BC^2 = AB^2 + AC^2$, треугольник $ABC$ — равнобедренный, $∠CAB = 90°$. Тогда высота, опущенная на сторону $BC$ будет равна половине $BC$, то есть $13$.
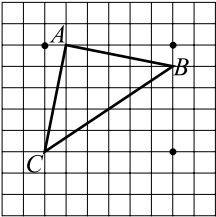
Задача 9
На клетчатой бумаге с размером клетки $1$ см $×$ $1$ см изображён треугольник $ABC$ (см. рис. ). Найдите длину его медианы, проведённой из вершины $B$ (в сантиметрах).
Решение
Длина медианы проведённой из $B$, равна половине длины гипотенузы в $△ABC, ∠B = 90°. AC^2 = AB^2 + BC^2; AC^2 = 144 + 25 = 169, AC = 13. m_B = {AC}/{2}= {13}/{2}=6.5$.
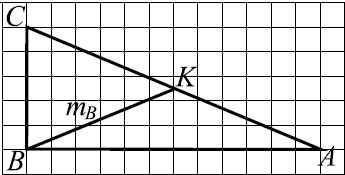
Задача 10
На клетчатой бумаге с размером клетки $1$ см $×$ $1$ см изображён треугольник $ABC$ (см. рис. ). Найдите длину его медианы, проведённой из вершины $B$ (в сантиметрах).
Решение
Длина медианы проведённой из $B$, равна половине длины гипотенузы в $△ABC, ∠B = 90°. AC^2 = AB^2 + BC^2; AC^2 = 36 + 64, AC^2 = 100, AC = 10. m_B = {AC}/{2}= 5. m_B = 5$.
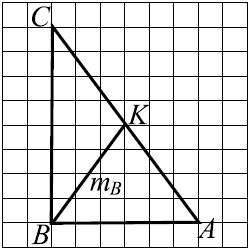
Задача 11
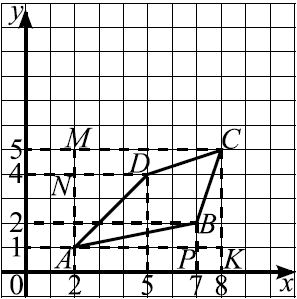
Найдите площадь четырёхугольника, вершины которого имеют координаты $(2;1)$, $(7;2)$, $(8;5)$, $(5;4)$ (см. рис. ).
Решение
$S_{ABCD} = S_{AKCM} - (S_{AND} + S_{NDCM}+S_{CBPK} + S_{APB}) = 6 · 4 -({1}/{2} · 3 · 3 + {3+ 6}/{2} · 1 + {1 + 4}/{2} · 1 + {1}/{2} · 5 · 1)= 24 - 14 = 10$.
Задача 12
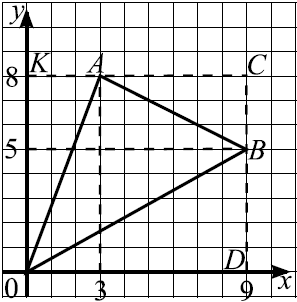
Найдите площадь треугольника, вершины которого имеют координаты $(0;0)$, $(3;8)$, $(9;5)$ (см. рис. ).
Решение
$S_{AOB} = S_{OKCD} - (S_{OKA} + S_{ACB} + S_{OBD}) = 9·8-({1}/{2}·8·3+{1}/{2}·6·3+ {1}/{2}·9·5) = 72-(12+9+22.5) = 72-43.5 = 28.5$
Задача 13
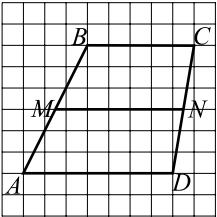
На клетчатой бумаге с размером клетки $1$ см $×$ $1$ см изображена трапеция (см. рис. ). Найдите длину средней линии трапеции.
Решение
Средняя линия трапеции равна полусумме оснований: $MN = {BC + AD}/{2} = {5 +2}/{7} = 6$.
Задача 14
На клетчатой бумаге с размером клетки $1× 1$ отмечены точки $A$, $B$ и $C$. Найдите квадрат расстояния от от точки $A$ до прямой $BC$.
Решение
Найдём стороны $△ABC$.
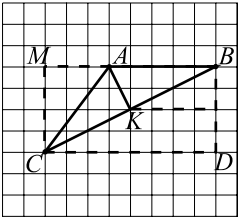
Из $△AСM : AC = √{AM^2 + MC^2} = √{9+16} = √{25}=5$;
Из $△BDC : BC = √{BD^2 + DC^2} = √{16+64} = √{80}=4√$.
$AB=5$.
Итак, $△ABC$ — равнобедренный, значит высота $AK$ является и медианой. Точка $K$ делит $BC$ пополам, $BK = {BC}/{2}=2√5$.
Из $△AKB : AK^2 = AB^2 - KB^2 = 25 - 4·5 = 5. AK^2 = 5$.
Задача 15
Найдите площадь закрашенной фигуры на координатной плоскости с размером клетки $1$ см $×$ $1$ см (см. рис. ).
Решение
Четырёхугольники $ABCD$ и $MNPQ$ — квадраты, так как:
1. $AB = √{9 + 9} = √{18}, BC = √{9 + 9} = √18, CD = √{9 + 9} = √18, AD = √{9 + 9} = √18$; аналогично $MN = NP = PQ = MQ = √8$, то есть $ABCD$ и $MNPQ$ — ромбы.
2. Диагонали $BD$ и $AC$ равны и диагонали $MP$ и $QN$ равны.
Площадь заштрихованной фигуры равна разности площадей квадра- тов со сторонами $√18$ и $√8$.
$S = S_1 - S_2 = AB^2 - MN^2 = (√18)^2 - (√8)^2 = 18 - 8 = 10$.
Задача 16
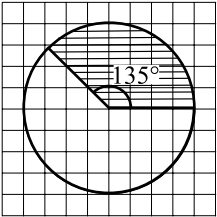
На клетчатой бумаге изображён круг (см. рис. ). Какова площадь круга, если площадь заштрихованного сектора равна $12$?
Решение
По условию площадь заштрихованной части круга равна 12, тогда площадь круга можно найти из формулы: $S{сектора} = S_{круга}360° · 135°; S_{круга} = {360 · S_{сектора}}/{135} = {360 · 12}/{135} = 32$.
Задача 17
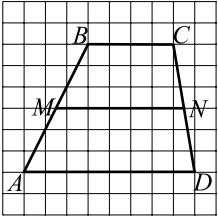
На клетчатой бумаге с размером клетки $1$ см $×$ $1$ см изображена трапеция (см. рис. ). Найдите длину средней линии трапеции.
Решение
Средняя линия трапеции равна полусумме оснований: $MN = {BC + AD}/{2} = {4 + 8}/{2} = 6$.
Задача 18
Найдите площадь четырёхугольника, вершины которого имеют координаты $(2;2)$, $(8;3)$, $(9;6)$, $(6;5)$ (см. рис. ).
Решение
Рассмотрим рисунок. $S_{ABCD}=S_{AMCN}-(S_{AKD}+S_{KDCN}+ $
$+S_{CMEB}+S_{ABE})=7⋅ 4-({1} / {2}⋅ 3⋅ 4+{4+7} / {2}⋅ 1+{1+4} / {2}⋅ 1+{1} / {2}⋅ 6⋅ 1)=$
$=28-(6+5{,}5+2{,}5+3)=28-17=11$.
Задача 19
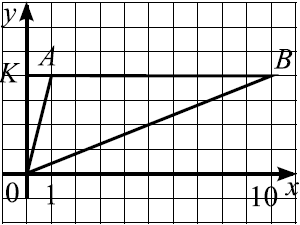
Найдите площадь треугольника, вершины которого имеют координаты $(0;0)$, $(1;4)$, $(10;4)$ (см. рис. ).
Решение
$S_{AOB} = {1}/{2}·OK·AB = {1}/{2}·4·9=18$
Задача 20
На клетчатой бумаге с размером клетки $1$ см $×$ $1$ см изображён прямоугольник (см. рис. ). Найдите радиус окружности, описанной около этого прямоугольника.
Решение
$ABCD$ по условию прямоугольник (см. рис. ), центр описанной окружности находится в точке пересечения диагоналей, то есть диагональ $AC$ является её диаметром, равным $6$, значит, радиус этой окружности равен $3$.
Рекомендуемые курсы подготовки

- 👻 Вспомнишь алгебраические преобразования
- 👻 Отработаешь линейные, квадратные и дробно-рациональные уравнения
- 👻 Покоришь движение по воде
- 👻 И в целом крайне продуктивно проведешь время
на бесплатном курсе Турбо ЕГЭ

