Задание 10. Прикладная планиметрия. ЕГЭ 2026 по математике (базовой)
Средний процент выполнения: 83.5%
Алгоритм решения задания 10:
Проанализируйте условие задачи и определите, какие геометрические фигуры в ней рассматриваются.
Выясните, какие элементы фигуры известны, а какие требуется найти.
Подберите соответствующие свойства или теоремы планиметрии, применимые к данной конфигурации.
Составьте последовательность рассуждений, связывающих известные и искомые величины.
Выполните вычисления на основе выбранных геометрических соотношений.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Рассмотрим колодец с «журавлём». Пусть короткое плечо имеет длину 2 м, длинное – 9 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Решение
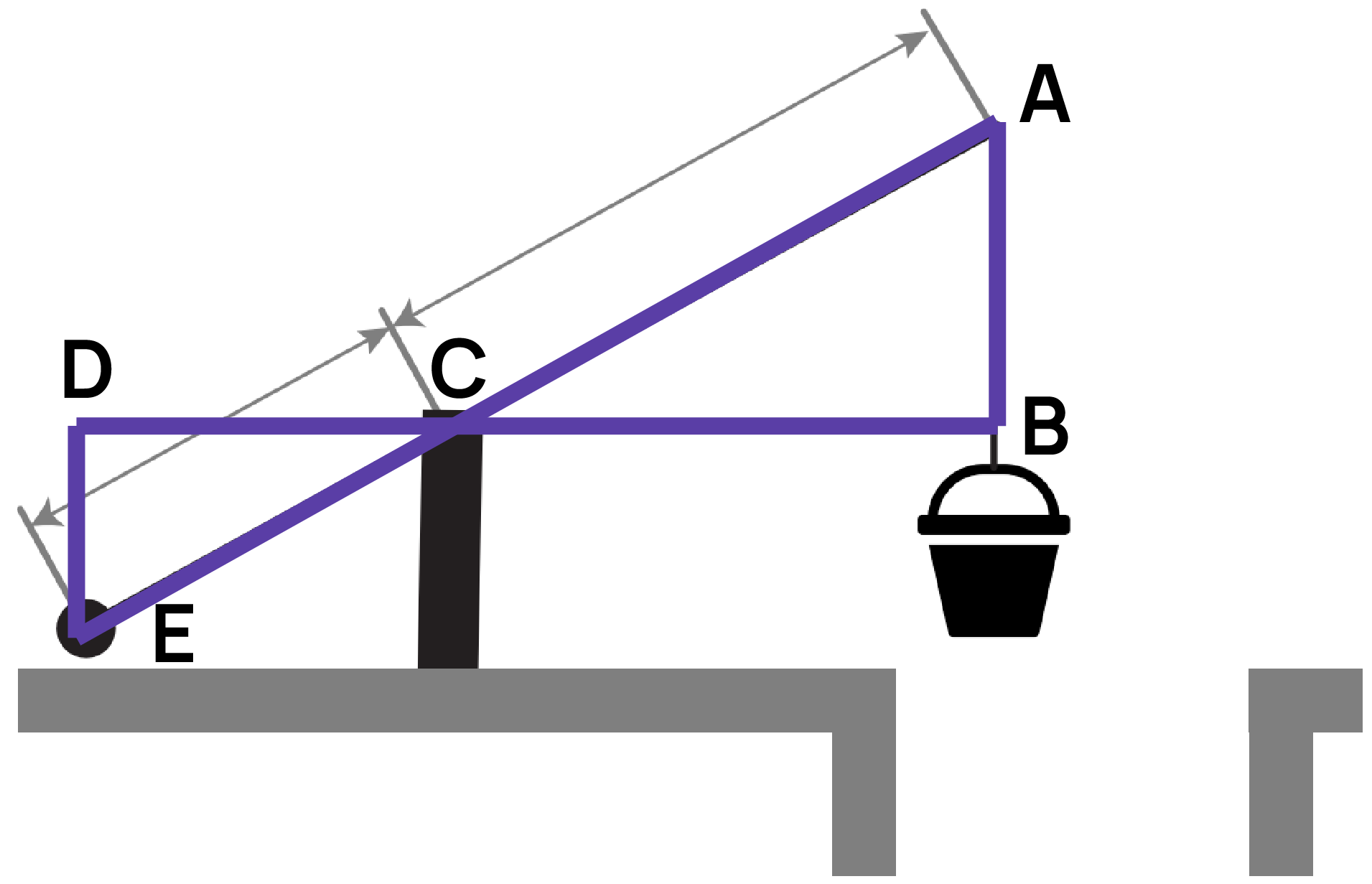
Введем дополнительные обозначения: DE - высота, на которую поднялось короткое плечо CE до положения CD, AB - высота, на которую опустилось длинное плечо AC до положения CB. Теперь можно рассмотреть данные треугольники.
Угол DCE равен углу ACB как вертикальные, угол EDC равен углу CBA как накрест лежащие углы при секущей DB параллельных прямых DE и AB. Тогда треугольники ABC и CDE подобны по двум углам.
Запишем отношение сходственных сторон: ${CE}/{AC}={DE}/{AB}=2/9=1/x->2x=9->x=4,5$
Задача 2
На расстоянии 5 м от столба высотой 4 м стоит человек, от которого падает тень длиной 3 м. Найдите рост человека.
Решение
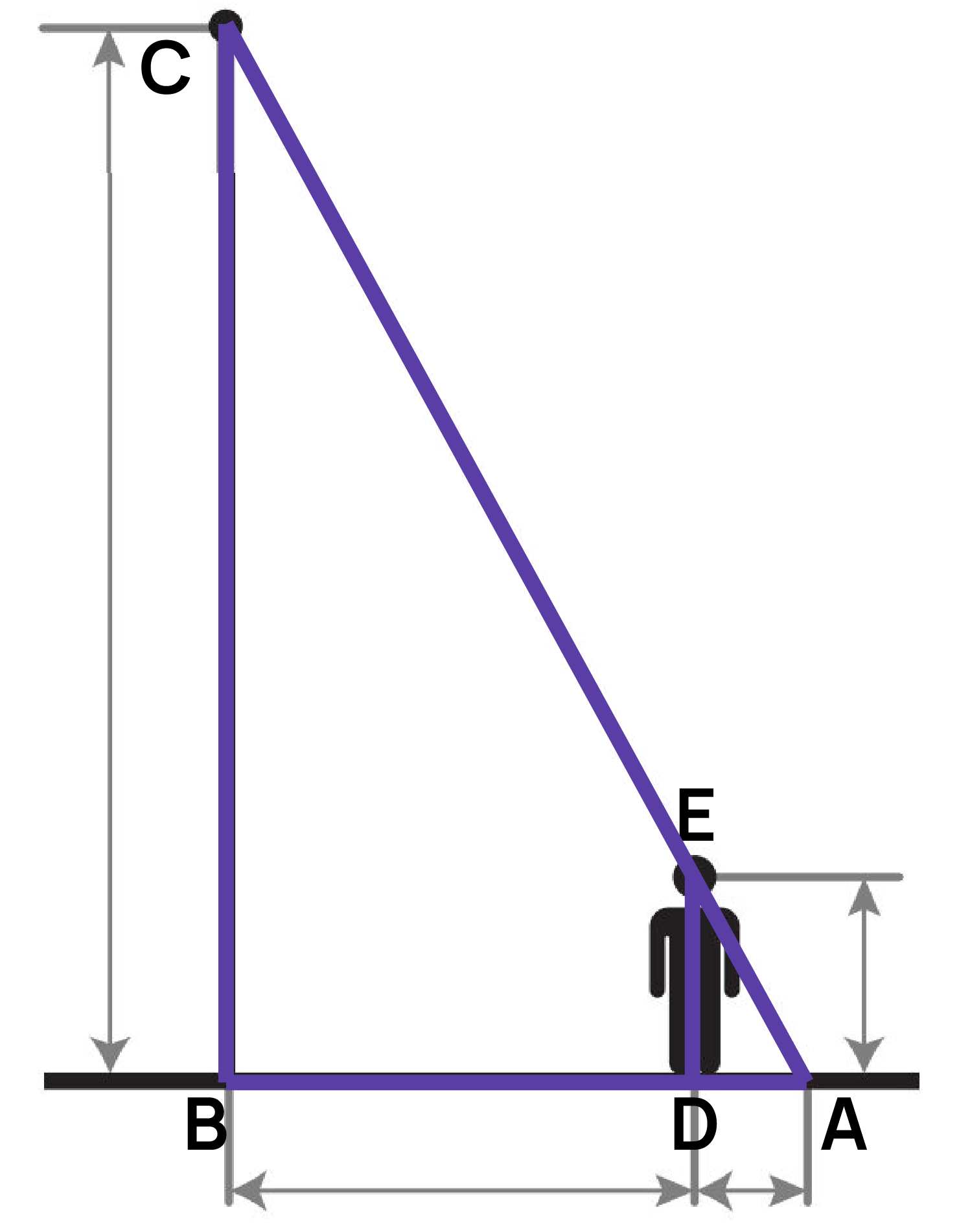
Добавим точки для удобства решения. Пусть A - точка конца тени, B - точка основания фонаря, C - точка верхушки фонаря, D - ноги человека, E - голова человека. Тогда получаются два треугольника: ABC - треугольник, образованный фонарем и концом тени человека, ADE - треугольник, образованный человеком и его тенью. Расмотрим треугольники ABC и ADE: угол A общий, углы CBA и EDA равны как соответственные при параллельных прямых BC и DE, значит, треугольники ABC и ADE подобны.
Запишем отношение сходственных сторон: ${BC}/{ED}={AB}/{AD}=4/x={5+3}/3->4⋅3=8⋅x->x=12/8=3/2=1,5$
Задача 3
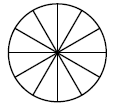
Колесо имеет 12 спиц. Углы между соседними спицами равны. Найдите величину наименьшего угла (в градусах), который образуют две соседние спицы.
Решение
Колесо имеет 12 спиц, и углы между соседними спицами равны. Поскольку углы между всеми спицами составляют полный круг, то сумма всех углов между соседними спицами равна 360°. Чтобы найти величину одного угла между двумя соседними спицами, нужно разделить 360° на количество спиц:
$$ {360°}/{12} = 30° $$
Ответ: 30°
Задача 4
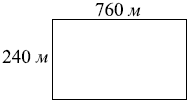
Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 760 м и 240 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.
Решение
1. Определение сторон, которые нужно огородить
Поскольку одна из длинных сторон (760 м) не требует забора, нам нужно оградить следующие стороны:
- Одна длинная сторона (760 м)
- Две короткие стороны (по 240 м каждая)
2. Вычисление длины забора
Теперь мы можем вычислить общую длину забора, складывая длины всех сторон, которые нужно огородить:
Длина забора = Длина одной длинной стороны + 2 × Длина короткой стороныПодставим значения:
Длина забора = 760 м + 2 × 240 мВыполним вычисления:
Длина забора = 760 м + 480 м = 1240 мЗадача 5
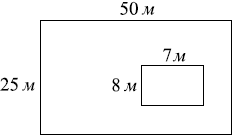
Дачный участок имеет форму прямоугольника со сторонами 50 метров и 25 метров. Дом, расположенный на участке, также имеет форму прямоугольника, стороны которого равны 8 и 7 м. Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
Решение
Для начала, давайте найдем площадь всего дачного участка и площадь дома, а затем вычтем площадь дома из площади участка, чтобы определить площадь оставшейся части.
1. Площадь дачного участка
Дачный участок имеет форму прямоугольника со сторонами 50 метров и 25 метров. Площадь прямоугольника вычисляется по формуле:
Площадь = Длина × ШиринаПодставим значения:
Площадь участка = 50 м × 25 м = 1250 м²2. Площадь дома
Дом также имеет форму прямоугольника со сторонами 8 метров и 7 метров. Вычислим его площадь по той же формуле:
Площадь дома = Длина × ШиринаПодставим значения:
Площадь дома = 8 м × 7 м = 56 м²3. Площадь оставшейся части участка
Теперь мы можем найти площадь оставшейся части участка, вычитая площадь дома из площади участка:
Площадь оставшейся части = Площадь участка - Площадь домаПодставим значения:
Площадь оставшейся части = 1250 м² - 56 м² = 1194 м²Ответ
Площадь оставшейся части дачного участка составляет 1194 квадратных метра.
Задача 6
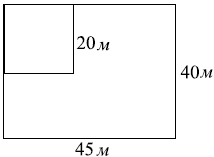
Дачный участок имеет форму прямоугольника со сторонами 40 метров и 45 метров. Хозяин планирует обнести его изгородью и отгородить такой же изгородью квадратный участок со стороной 20 м. Найдите суммарную длину изгороди в метрах.
Решение
Поскольку мы ходим огородить некую фигуру, речь идетт о периметре. Тогда:
1) $45+40+45+40=170$ - длина изгороди внешней части
2)$170+20+20=210$ - к сумме длин внешней изгороди прибавили два отрезка по 20 метов, которые расположены на участке.
Таким образом, потребуется 210 метров изгороди.
Задача 7
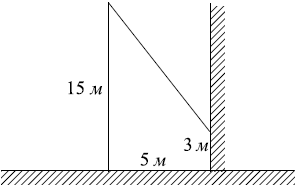
От столба высотой 15 м к дому натянут провод, который крепится на высоте 3 м от земли. Расстояние от дома до столба 5 м. Найдите длину провода. Ответ дайте в метрах.
Решение
- Определение высоты треугольника:
- Применение теоремы Пифагора:
- Подставим значения:
- Найдем длину провода:
h = 15 м - 3 м = 12 м.
L2 = h2 + d2.
L2 = 122 + 52.
L2 = 144 + 25 = 169.
L = √169 = 13 м.
Ответ:
Длина провода составляет 13 метров.
Задача 8
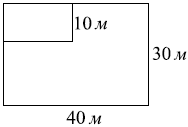
Дачный участок имеет форму прямоугольника со сторонами 30 метров и 40 метров. Хозяин планирует обнести его изгородью и отгородить такой же изгородью квадратный участок со стороной 10 м. Найдите суммарную длину изгороди в метрах.
Решение
- Рассчитаем периметр прямоугольного участка:
- Рассчитаем периметр квадратного участка:
- Найдем суммарную длину изгороди:
Pпрям = 2 * (длина + ширина)
Pпрям = 2 * (40 + 30) = 2 * 70 = 140 метров
Pкв = 4 * сторона
Pкв = 4 * 10 = 40 метров
Pсум = Pпрям + Pкв - (2 * сторона)
Pсум = 140 + 40 - (2 * 10)
Pсум = 140 + 40 - 20
Pсум = 160 метров
Ответ:
Суммарная длина изгороди составляет: 160 метров.
Задача 9
Пол комнаты, имеющий форму прямоугольника со сторонами 5 м и 8 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
Решение
Сначала найдем площадь пола комнаты:
$$S_{пол} = 5 м ∙ 8 м = 40 м^2$$Теперь переведем площадь в квадратные сантиметры:
$$40 м^2 = 400 000 см^2$$Теперь найдем площадь одной дощечки:
$$S_{дощечки} = 10 см ∙ 20 см = 200 см^2$$Чтобы найти количество дощечек, делим общую площадь пола на площадь одной дощечки:
$$N = 400000/200 = 2000 $$Значит, потребуется 2000 дощечек.
Задача 10
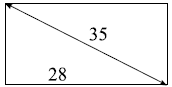
Диагональ прямоугольного экрана равна 35 см, а ширина экрана 28 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
Решение
$AB=35, BC=28, AC-?$
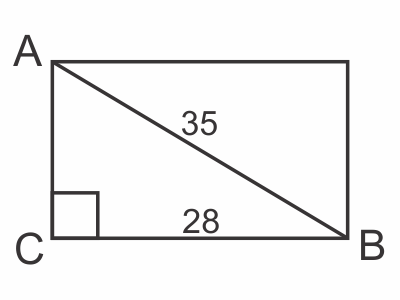
$△ABC$- прямоугольный, $∠ACB=90°$, тогда по теореме Пифагора $AC=√{AB^2-BC^2}$,
$AC=√{35^2-28^2}=21$.
Задача 11
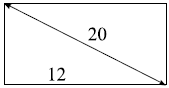
Диагональ прямоугольного экрана равна 20 см, а ширина экрана - 12 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
Решение
Все углы прямоугольника прямые, значит по теореме Пифагора $α=√{20^2-12^2}=16$
Задача 12
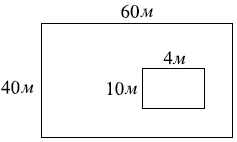
Дачный участок имеет форму прямоугольника со сторонами 60 метров и 40 метров. Дом, расположенный на участке, также имеет форму прямоугольника, стороны которого равны 10 и 4 м. Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
Решение
$S=S_1-S_2=40·60-10·4=2400-40=2360 м^2$
Задача 13
Два садовода, имеющие прямоугольные участки размерами 40 м на 50 м с общей границей, договорились и сделали общий круглый пруд площадью 120 квадратных метров, причём граница участков проходит точно через центр пруда. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
Решение
- Вычислим площадь одного участка:
- Общая площадь двух участков:
- Вычислим площадь пруда на каждом участке:
- Вычислим оставшуюся площадь на каждом участке:
Площадь одного участка равна:
Площадь = длина × ширина = 40 м × 50 м = 2000 м².
Общая площадь = 2000 м² + 2000 м² = 4000 м².
Поскольку пруд имеет общую площадь 120 м², каждая половина занимает:
60 м².
Оставшаяся площадь = Площадь участка - Площадь пруда на участке.
Оставшаяся площадь = 2000 м² - 60 м² = 1940 м².
Ответ:
Площадь оставшейся части участка каждого садовода составляет 1940 квадратных метров.
Задача 14
Два садовода, имеющие прямоугольные участки размерами 50 м на 20 м с общей границей, договорились и сделали общий круглый пруд площадью 80 квадратных метров, причём граница участков проходит точно через центр пруда. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
Решение
Площадь каждого участка изначально равна:
50 * 20 = 1000 м²
Общий круглый пруд имеет площадь 80 м², и граница участков делит пруд ровно пополам. Следовательно, площадь пруда, приходящаяся на каждый участок:
80 / 2 = 40 м²
Оставшаяся площадь каждого участка:
1000 - 40 = 960 м²
Ответ: площадь оставшейся части участка каждого садовода составляет 960 м².
Задача 15
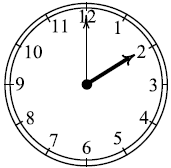
Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 2:00?
Решение
Часовая стрелка за один час проходит 30°, поэтому в 2:00 она будет находиться под углом:
$$2 * 30 = 60°$$
Минутная стрелка за один полный круг (60 минут) проходит 360°. За 0 минут она будет находиться на отметке 0°.
Угол между стрелками:
$$60 - 0 = 60°$$
Так как угол меньше 180°, он является наименьшим.
Ответ: 60°
Задача 16
Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите величину наименьшего угла (в градусах), который образуют две соседние спицы.
Решение
1. Общая величина угла в круге: Полный круг составляет 360 градусов.
2. Количество спиц: В данном случае у нас 18 спиц.
3. Вычисление угла между соседними спицами:
Угол между двумя соседними спицами можно найти, разделив полный угол на количество спиц:
Угол = 360° / n
где n — количество спиц.
4. Подставляем значения:
Угол = 360° / 18 = 20°
Ответ:
Таким образом, величина наименьшего угла, который образуют две соседние спицы, равна 20 градусов.
Задача 17
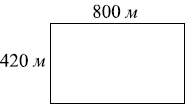
Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 800 м и 420 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.
Решение
$l=2·420+800=840+800=1640$(м)
Задача 18
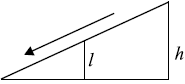
Столб подпирает детскую горку посередине. Найдите высоту $l$ этого столба, если высота $h$ горки равна $4$ м. Ответ дайте в метрах.
Решение
Задача 19
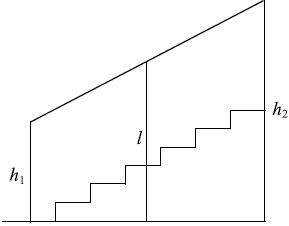
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту $l$ этого столба, если наименьшая высота $h_1$ перил равна 50 см, а наибольшая высота $h_2$ равна 100 см. Ответ дайте в сантиметрах.
Решение
Задача 20

От столба высотой 29 м к дому натянут провод, который крепится на высоте 5 м от земли. Расстояние от дома до столба 7 м. Найдите длину провода. Ответ дайте в метрах.
Решение
Рекомендуемые курсы подготовки

- 👻 Вспомнишь алгебраические преобразования
- 👻 Отработаешь линейные, квадратные и дробно-рациональные уравнения
- 👻 Покоришь движение по воде
- 👻 И в целом крайне продуктивно проведешь время
на бесплатном курсе Турбо ЕГЭ

