Задание 11. Прикладная стереометрия. ЕГЭ 2026 по математике (базовой)
Средний процент выполнения: 81.7%
Алгоритм решения задания 11:
Определите, какое пространственное тело или фигура описаны в условии задачи.
Выясните, какие элементы фигуры заданы и какие геометрические величины требуется найти.
Рассмотрите плоские сечения или грани фигуры и установите, какие планиметрические факты к ним применимы.
Используйте известные формулы и соотношения для вычисления длин, площадей или других величин.
Проверьте, что полученные значения соответствуют геометрическому смыслу задачи.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
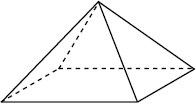
Здание имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 140 м, а высота - 88 м. Сторона основания макета, который является точной копией здания, равна 14 см. Найдите высоту макета. Ответ дайте в сантиметрах.
Решение
$a_1=140_{a}$; $h_1=88$м; $a_2=14$см; $h_2-?$
${a_1}/{h_1}={a_2}/{h_2}$ , $h_2={a_2h_1}/a_1={14·88}/{140}=8.8$(см)
Задача 2
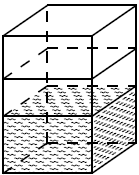
В бак, имеющий форму прямой призмы, налито 6 л воды. После полного погружения детали в воду уровень воды поднялся в 1.5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
Решение
Изначальный объем воды в баке составляет:
6 л = 6 * 1000 = 6000 см³
После погружения детали уровень воды увеличился в 1.5 раза, значит общий объем воды стал:
6000 * 1.5 = 9000 см³
Объем детали равен разности между конечным объемом воды и изначальным объемом:
9000 - 6000 = 3000 см³
Ответ: объем детали составляет 3000 см³.
Задача 3
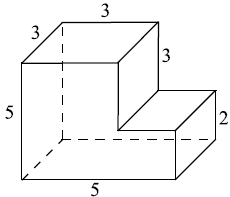
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Решение
Чтобы решить эту задачу, разобьем фигуру на два параллелепипеда: нижний со сторонами 5(длина), 3(ширина) и 2 (высота) и верхний со сторонами 3(длина), 3(ширина) и 3 (высота): $V=V_1+V_2=5·3·2+3·3·3=30+27=57(см^3)$.
Задача 4
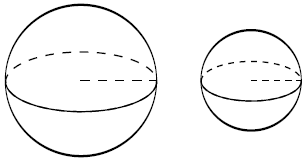
Однородный шар диаметром 3 см имеет массу 324 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
Решение
$m=pv;$ $m_1=p_1v_1=p_1·4/3πR_1^3$
$p_1=p_2$ $m_2=p_2v_2=p_2·4/3πR_1^3$
${m_1}/{m_2}={p_1·4/3πR_1^3}/{p_2·4/3πR_2^3}$
${m_1}/{m_2}={R_1^3}/{R_2^3};$ $m_2={m_1·R_2^3}/{R_1^3}$
$m_2={324·2^3}/{3^3}={324·8}/{27}=12·8=96$.
Задача 5
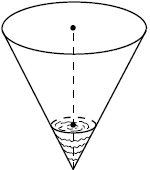
В сосуде, имеющем форму конуса, уровень жидкости достигает ${1}/{4}$ высоты. Объём сосуда равен $640$ мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
Решение
Шаг 1: Формула объема конуса
Объем конуса рассчитывается по формуле:
V = (1/3) * π * r² * h
Шаг 2: Объем жидкости в сосуде
Когда уровень жидкости достигает 1/4 высоты, объем налитой жидкости будет равен:
Vжидкости = V * (h'/h)3
где h' = 1/4 * h
Шаг 3: Вычисление объема налитой жидкости
Vжидкости = 640 * (1/4)3 = 640 * (1/64) = 10 мл
Ответ:
Объем налитой жидкости равен: 10 мл.
Задача 6
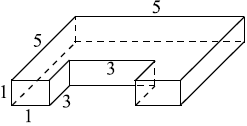
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.
Решение
Для нахождения площади поверхности параллелепипеда с вырезанным куском необходимо рассчитать площадь поверхности всего параллелепипеда и затем вычесть площадь вырезанного куска.
1. Площадь поверхности всего параллелепипеда:
Формула для площади поверхности прямоугольного параллелепипеда:
P = 2(ab + ac + bc),
где:- a = 5 см (длина)
- b = 5 см (ширина)
- c = 1 см (высота)
Подставим значения в формулу:
P = 2(5 × 5 + 5 × 1 + 5 × 1) = 2(25 + 5 + 5) = 2(35) = 70 см².
2. Площадь поверхности вырезанного куска:
Размеры вырезанного куска: 3 × 3 × 1.
Площадь поверхности вырезанного куска:
Pw = 2(3 × 3 + 3 × 1 + 3 × 1) = 2(9 + 3 + 3) = 2(15) = 30 см².
3. Корректировка площади поверхности:
При вырезании куска мы убираем его площадь, но добавляем площадь его внутренней стороны, которая не была включена в первоначальную площадь. Площадь внутренней стороны равна площади основания вырезанного куска (3 × 3):
Pвн = 3 × 3 = 9 см².
Итоговая площадь поверхности:
Pитог = P - Pw + Pвн
Pитог = 70 - 30 + 9 + 9 = 58 см².
Ответ:
Площадь поверхности детали составляет:
58 квадратных сантиметров.
Задача 7
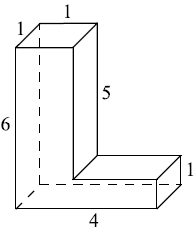
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Решение
$V_{общ}=V_1+V_2=4·1·1+1·1·5=9$
Задача 8
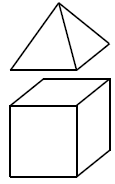
К призме, основание которой квадрат со стороной 3, приклеили правильную четырёхугольную пирамиду с ребром 3 так, что квадратные грани совпали. Сколько граней у получившегося многогранника?
Решение
- Определение граней призмы:
- Определение граней пирамиды:
- Объединение фигур:
- Подсчёт общего количества граней:
У квадратной призмы есть:
- 2 квадратные грани (верхняя и нижняя).
- 4 прямоугольные грани (боковые).
Итого: 6 граней.
У правильной четырёхугольной пирамиды есть:
- 1 квадратная грань (основание).
- 4 треугольные грани (боковые).
Итого: 5 граней.
При приклеивании пирамиды к призме основание пирамиды совпадает с верхней гранью призмы.
Это означает, что мы не добавляем новую грань за счёт основания пирамиды.
Количество граней у получившегося многогранника:
От призмы:
- 1 нижняя квадратная грань (основание).
- 4 боковые прямоугольные грани.
От пирамиды:
- Учитываем только боковые треугольные грани: 4.
Итого:
1 + 4 + 4 = 9.
Ответ:
У получившегося многогранника 9 граней.
Задача 9
Однородный шар диаметром 1 см имеет массу 63 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
Решение
$d_1=1$см ; $m_1=63$гр ; $p_1=p_2$
$d_2=2$см ; $m_2-?$
${m_1}/{m_2}={p_1·v_1}/{p_2·v_2}={v_1}/{v_2}={4/3πR_1^3}/{4/3πR_2^3}={({R_1}/{R_2})}^3={({d_1}/{d_2})}^3=(1/2)^3=1/8$
$m_2=8m_1=8·63=504$ (гр)
Задача 10
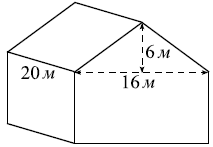
Двускатную крышу дома, имеющего в основании прямоугольник, необходимо полностью покрыть рубероидом. Высота крыши равна 6 м, длины стен дома равны 16 и 20 м. Найдите, сколько рубероида (в квадратных метрах) нужно для покрытия этой крыши, если скаты крыши равны.
Решение
- Определение длины основания одного ската:
- Вычисление длины ската:
- Определение площади одного ската:
- Общая площадь крыши:
Для стены длиной 16 м: bA = lA/2 = 16/2 = 8 м.
Для стены длиной 16 м: sA = √(h² + bA²) = √(6² + 8²) = √(36 + 64) = √100 = 10 м.
SA= 10 * 20 = 200 м² .
S{общая}= SA*2=(200)*2=400 м².
Ответ:
Для покрытия двускатной крыши потребуется 400 квадратных метров рубероида.
Задача 11
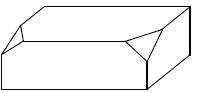
От кирпича отпилили 2 его вершины. Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Решение
Для того чтобы ответить на вопрос, давайте представим, как выглядит кирпич и что происходит при удалении двух его вершин.
Кирпич (или прямоугольный параллелепипед) имеет:
- 6 прямоугольных граней,
- 12 рёбер,
- 8 вершин.
Когда от кирпича отпиливают две его вершины, мы фактически создаём новые грани, заменяя эти вершины плоскостью, которая проходит через рёбра, соединяющие отпиленные вершины.
Теперь давайте посчитаем:
- После удаления двух вершин, количество граней увеличивается. Каждая удалённая вершина создаёт новую грань. Так как удалены две вершины, это добавляет две новые грани.
- Изначально у кирпича было 6 граней, но после удаления вершин число граней увеличится на 2, так что общее количество граней будет: $6 + 2 = 8$.
Таким образом, у получившегося многогранника будет 8 граней.
Ответ: 8 граней.
Задача 12
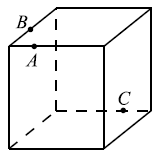
Плоскость, проходящая через точки A, B и C, разбивает куб на два многогранника. Сколько вершин у получившегося многогранника с большим числом граней?
Решение
Куб имеет 8 вершин, 12 рёбер и 6 граней.
Когда плоскость проходит через три точки (A, B и C), она может разбить куб на два многогранника. Если плоскость проходит через три вершины куба, то один из получившихся многогранников будет иметь:
- 4 вершины от плоскости (через которые она проходит) и 6 дополнительных вершин куба.
- Таким образом, общее количество вершин у многогранника с большим числом граней составит 10.
Ответ: У многогранника с большим числом граней 10 вершин.
Задача 13
Сосуд в виде цилиндра наполнен жидкостью, уровень которой $18$ см. Найдите, на какой высоте будет находиться уровень этой же жидкости, если её перелить в другой цилиндрический сосуд, радиус основания которого в $2$ раза больше радиуса первого? Ответ выразите в сантиметрах.
Решение
$h_{ж_1}=18;R_1;R_2=2R_1;h_2-?V_1=V_2$
$πR_1^2h_1=πR_2^2h_2$
$h_2={R_1^2h_1}/{R_2^2}={R_1^2·18}/{4R_1^2}={18}/{4}=4,5$
Задача 14
Найдите расстояние между вершинами $A_1$ и $E$ многогранника, изображённого на рисунке. Все двугранные углы многогранника — прямые.
Решение
т.к.$AA_1⊥(ABC),$ то $AA_1⊥AE, ∆AEA_1$ - прямоугольный, $∠A_1AE=90°$
Рассмотрим $∆AFE:∠AFE=90°, AF=6+5=11; FE=4+6=10;$
по теореме Пифагора $AE^2=AF^2+FE^2=11^2+10^2=121+100=221$
по теореме Пифагора из $∆AA_1E:A_1E=√{AA_1^2+AE^2}=√{2^2+221}=√{225}=15$
Задача 15
В цилиндрическом сосуде уровень жидкости достигает $45$ см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в $3$ раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение
Объём воды после переливания остаётся тем же: $V_1 = V_2$; $π r_1^2 ⋅ 45 = π r_2^2 ⋅ h_2$. Так как диаметр второго сосуда в $3$ раза больше диаметра первого, то и радиус второго втрое больше радиуса первого:
$45r_1^2 = (3r_1)^2 ⋅ h_2$; $45r_1^2 = 9r_1^2 ⋅ h_2$; $h_2 = 5$.
Задача 16
В цилиндрическом сосуде уровень жидкости достигает $20$ см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза меньше диаметра первого? Ответ выразите в сантиметрах.
Решение
$h_1=20; R_1; d_1;$
$h_2-?d_2={1}/{2}d_1,$ значит $R_2={1}/{2}R_1$
$V_1=V_2$
$πR_1^2h_1=πR_2^2h_2$
$h_2={R_1^2h_1}/{R_2^2}={R_1^2h_1}/{({1}/{2}R_1)^2}=4h_1=80$
Задача 17
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые)
Решение
Рассмотрим данный многогранник как прямую призму, в основании которой лежит восьмиугольник.
$S_{пов}=S_{бок.пов}+2S_{осн}=P_{осн}·h+2(S_1+S_2)=(10+4)·2·6+2(10·2+6·2)=14·12+2·32=168+64=232$
Задача 18
В сосуде, имеющем форму конуса, уровень жидкости достигает ${1} / {3}$ высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение
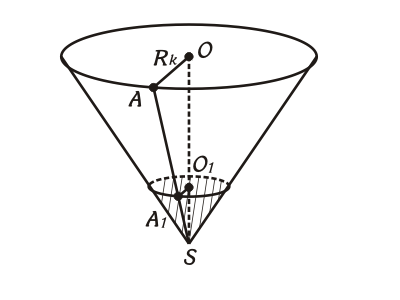
$V_{ж_1}=70; h_ж={1}/{3}h_k$
$V_{ж_2}-? V_{ж_1}+V_{ж_1]2}=V_{конуса}$
$OA=R_{конуса}; O_1A_1=R_1$
$∆SA_1O_1∼∆SAO; {AO}/{A_1O_1}={OS}/{O_1S}=3$
$R_k=AO=3A_1O_1=3R_1; V_{конуса}={1}/{3}πR_k^2·h_k={1}/{3}π·(3R_1)^2·3h_ж=$
$=27·{1}/{3}πR_1^2h_ж=27V_{ж_1}=27·70=1890$
$V_{ж_2}=V_k-V_{ж_1}=1890-70=1820$
Задача 19
Цилиндр высотой $5$ см, радиусом основания $6$ см наполнили доверху водой (см. рис.). На каком уровне (в см) будет находиться вода в другом цилиндре с радиусом основания в $2$ раза меньше радиуса первого цилиндра?
Решение
$h_1=5;R_1=6;V_1=V_2$
$h_2-?R_2={1}/{2}R_1={1}/{2}·6=3$
$V_1=πR_1^2h_1=π·6^2·5=180π$
$V_2=πR_2^2h_2=π·3^2·h_2=9πh_2$
$9πh_2=180π$
$h_2=20$
Задача 20
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение
8*5*2 + 2*4*5 = 80 + 40 = 120
Рекомендуемые курсы подготовки

- 👻 Вспомнишь алгебраические преобразования
- 👻 Отработаешь линейные, квадратные и дробно-рациональные уравнения
- 👻 Покоришь движение по воде
- 👻 И в целом крайне продуктивно проведешь время
на бесплатном курсе Турбо ЕГЭ

