Задание 12. Задачи по планиметрии. ЕГЭ 2026 по математике (базовой)
Средний процент выполнения: 74.1%
Алгоритм решения задания 12:
Определите, какие плоские геометрические фигуры рассматриваются в условии задачи.
Установите взаимное расположение элементов фигуры и их основные свойства.
Подберите подходящие теоремы или свойства планиметрии, применимые к данной ситуации.
Выразите искомые величины через известные, используя геометрические соотношения.
Оцените полученный результат с точки зрения размеров и формы фигуры.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
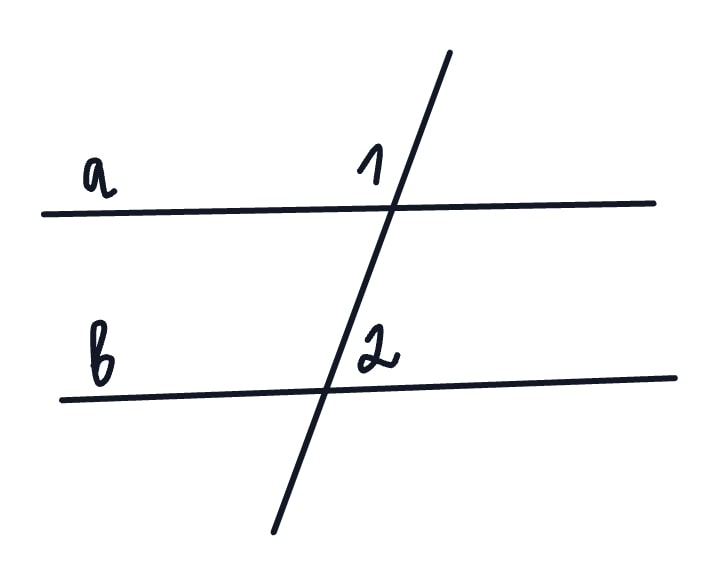
Прямые a и b параллельны. Найдите угол 2, если угол 1 равен $112°$. Ответ дайте в градусах.
Решение
Сначала найдем вертикальный угол для угла 1. Назовем его углом 3. Помним, что вертикальные углы равны. Углы 2 и 3 внутренние односторонние, а значит их сумма равна 180 градусам. Получаем: $112°+x=180°$, $x=68°$
Задача 2
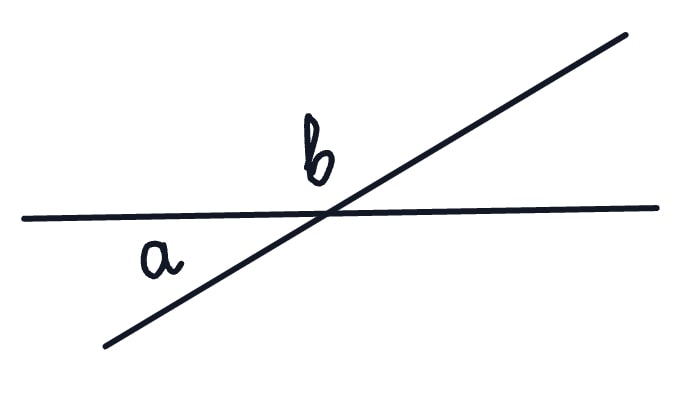
По рисунку найдите угол b, если известно, что угол $b = 5a$.
Решение
На рисунке изображены смежные углы, а значит их сумма равна 180 градусам: $а+b=180°$. Так как по условию угол b равен 5а, значит в наше уравнение вместо b подставляем 5а. Получаем: $а+5а=180°$ $6а=180°$ $а=30°$. Мы нашли угол а, но в задаче нужно найти угол b: $b=5·30°$ $b=150$
Задача 3
Один из внешних углов треугольника равен $80^°$. Углы, не смежные с данным внешним углом, относятся как $2:3$ (см. рис.). Найдите наибольший из них. Ответ дайте в градусах.
Решение
Сумма углов, не смежных с данным внешним углом, равна величине этого внешнего угла, то есть $∠ A+∠ C=80°$. Обозначим $∠ A=2x$, $∠ C=3x$. $2x+3x=80$, $5x=80$, $x=16$. $∠ C=3x=3⋅ 16=48°$ — наибольший из углов $A$ и $C$.
Задача 4
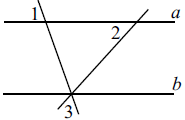
Прямые a и b параллельны. Найдите угол 2, если угол 1 равен $70°$, а угол 3 равен $71°$. Ответ дайте в градусах.
Решение
Сначала найдем вертикальный угол для угла 1, затем вертикальный угол для угла 3. Помним, что вертикальные углы равны. Найденные углы находятся внутри образовавшегося треугольника. Сумма углов в треугольнике равна 180 градусам. Отсюда составляем уравнение и решаем его: $70°+71°+x=180°$, $x=39°$
Задача 5
Площадь треугольника равна $72$, две его стороны равны $9$ и $24$. Найдите большую высоту этого треугольника.
Решение
Для нахождения высоты треугольника, используем формулу площади:
$$ S = 1/2 ∙ a ∙ h $$ Где $S$ - площадь треугольника, $a$ - основание, $h$ - высота к этому основанию.Рассмотрим две стороны: пусть $9$ будет основанием. Тогда:
$$ 72 = 1/2 ∙ 9 ∙ h_1 $$Решим уравнение для $h_1$:
$$ 72 = 9/2 ∙ h_1 => h_1 = 72 ∙ 2/{9} = 16 $$Теперь найдем высоту, соответствующую стороне $24$. Пусть это будет $h_2$:
$$ 72 = 1/2 ∙ 24 ∙ h_2 $$Решим уравнение для $h_2$:
$$ 72 = 12 ∙ h_2 => h_2 = 72/12 = 6 $$Таким образом, большая высота треугольника равна $16$.
Задача 6
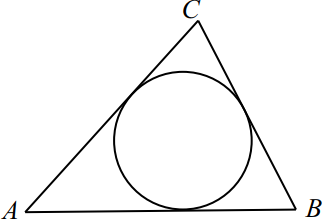
Окружность, вписанная в равнобедренный треугольник $ABC$, касается боковой стороны в точке $K$ (см. рис.). Найдите длину отрезка $CK$, если известно, что периметр треугольника равен $36$ и основание $AB$ равно 10.
Решение
$△ABC$ - равнобедренный, значит, $AC = CB$.
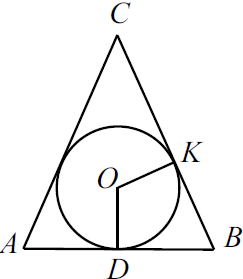
$P_{ABC} = AC+CB+AB, 36=2·BC+10; BC = 13$.
$AB=2DB, DB={10}/{2}=5$
Но $DB = KB$ (отрезки касательных к окружности, проведённые из одной точки, равны). $KB = 5, CK = BC - KB = 13 - 5 = 8$.
Задача 7
В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=9$, $\cos A={3} / {7}$ (см. рис.). Найдите $AB$.
Решение
$cosA = {AC}/{AB}, AB = {AC}/{cosA} = {9}/{{3}/{7}} = {9 · 7}/{3} = 21$.
Задача 8
В треугольнике $ABC$ $AC=BC$, $AH$ — высота, $AB=15$,
$\sin ∠ BAC=0{,}6$ (см. рис.). Найдите $BH$.
Решение
В равнобедренном треугольнике углы при основании равны.
$∠BAC = ∠ABC, sin ∠ABC = {AH}/{AB}, AH = AB sin ∠ABC. AH = 15 · 0.6 = 9$.
Из $△AHB: HB = √{AB^2 - AH^2} = √{225 - 81} = √{144} = 12$.
Задача 9
Два угла треугольника равны $48^°$ и $64^°$ (см. рис.). Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Решение
1) Так как сумма углов треугольника $ABC$ равна $180°$, то
$∠ C=180°-∠ A-∠ B=180°-48°-64°=68°$ (см. рис.). 2) Так как сумма углов четырёхугольника $CFOH$ равна $360°$, то
$∠ FOH=360°-∠ C-90°-90°=360°-68°-180°=112°$.
Задача 10
Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $AOM$ равен $28^°$. Найдите вписанный угол $MNB$. Ответ дайте в градусах.
Решение
$∠AOM$ — центральный, он измеряется дугой $AM$, то есть $︶AM = 28°$. $AB$ — диаметр, значит $︶AMB = 180°$, а $︶MB = 180° - 28° = 152°$. $∠MNB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠MNB = 76°$.
Задача 11
В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=6$, $\sin A={5} / {9}$ (см. рис.). Найдите $AB$.
Решение
$sin A = {BC}/{AB}, AB = {BC}/{sin A} = {6}/{{5}/{9}} = {6· 9}/{5} = {54}/{5} = 10.8$.
Задача 12
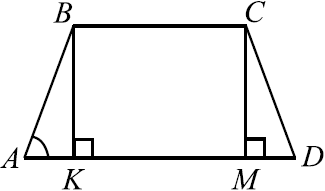
Основания равнобедренной трапеции равны $15$ и $9$. Высота трапеции равна $6$. Найдите тангенс острого угла.
Решение
Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ - высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.
$tg ∠BAD = {BK}/{AK}, AK = {AD - BC}/{2} = {15 - 9}/{2} = 3, BK = 6$ (по условию). $tg ∠BAD = {6}/{3} = 2$.
Задача 13
В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=4√ {7}$, $\tg A={√ {3}} / {2}$ (см. рис.). Найдите $AB$.
Решение
$\tg A={BC} / {AC}$, ${√ {3}} / {2}={BC} / {4√ {7}}$, $BC=2√ {21}$. $AB^2=AC^2+BC^2$; $AB^2=16⋅ 7+4⋅ 21$, $AB^2=112+84=196$, $AB=14$.
Задача 14
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^°$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.
Решение
Пусть в $▵ ABC$ $∠ C=30°$, $AC=BC=7$ (см. рис.). $S_{ACB}={1} / {2} AC⋅ CB⋅ \sin ∠ ACB={1} / {2}⋅ 7⋅ 7⋅ \sin 30°={1} / {2}⋅ 49⋅ {1} / {2}={49} / {4}=12{,}25$.
Задача 15
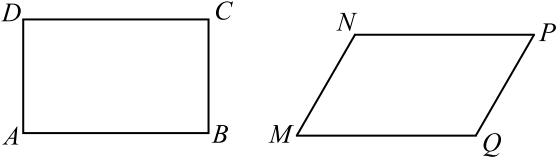
Параллелограмм и прямоугольник имеют одинаковые стороны. Сколько градусов составляет острый угол параллелограмма, если его площадь относится к площади прямоугольника как $1:√ {2}$?
Решение
Пусть $ABCD$ — прямоугольник, $MNPQ$ — параллелограмм (см. рис.).
$S_{MNPQ}={1} / {√ {2}} S_{ABCD}$, $S_{MNPQ}=MN⋅ MQ⋅ \sin ∠ NMQ$. $S_{ABCD}=AB⋅ AD$, но $MN=AD$, $AB=MQ$ (по условию). Тогда $MN⋅ MQ⋅ \sin ∠ NMQ={1} / {√ {2}} MN⋅ MQ$ (по условию). $\sin ∠ NMQ={1} / {√ {2}}$, $∠ NMQ=45°$.
Задача 16
Периметр треугольника равен $73$, а радиус вписанной окружности равен $4$. Найдите площадь этого треугольника.
Решение
$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {73}/{2} · 4 = 146$.
Задача 17
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь относится к площади прямоугольника как $√ {3}:2$.
Решение
Пусть $ABCD$ — прямоугольник, $MNPQ$ — параллелограмм.
$S_{MNPQ} = {√3}/{2}S_{ABCD}, S_{MNPQ} = MN · MQ · sin ∠NMQ$.
$S_{ABCD} = AB · AD$, но $MN = AD, AB = MQ$ (по условию).
Тогда $MN · MQ · sin ∠NMQ = {√3}/{2} MN · MQ$ (по условию).
$sin ∠NMQ = {√3}/{2}, ∠NMQ = 60°$.
Задача 18
Угол $ACO$ равен $32^°$. Его сторона $CA$ касается окружности с цент-
ром в точке $O$. Сторона $CO$ пересекает окружность в точках $B$ и $D$ (см. рис.). Найдите градусную меру дуги $AD$ окружности, заключённой внутри этого угла. Ответ дайте в градусах.
Решение
$∠ AOC=90°-∠ ACO$, так как $∠ OAC=90°$ (радиус, проведённый в точку касания, перпендикулярен касательной). $∠ AOC=90°-32°=58°$. $∠ AOC$ — центральный и измеряется дугой $AB$, то есть $⌣ AB=58°$. Отсюда: дуга $AD$ равна $180°-58°=122°$, так как дуга $DB=180°$.
Задача 19
В треугольнике $ABC$ $AC=BC$, $AB=15$
и $\tg ∠ BAC={2√ {5}} / {5}$ (см. рис.). Найдите высоту $AH$.
Решение
$tg ∠BAC = {CK}/{AK}, AK = {15}/{2}, CK = AK · tg ∠BAC={15}/{2}, {15}/{2}· {2√5}/{5} = 3√5$.
Найдём $AC$ из $△ACK$:
$AC = √{CK^2 + AK^2} = √{9·5+{225}/{4}} = √{{180+225}/{4}} = {9√5}/{2}; AC = BC$ (по условию), $BC = {9√5}/{2}$.
$S_{ABC} = {AB ·CK}/{2}, S_{ABC} = {CB· AH}/{2} ; AB · CK = CB · AH , AH = {AB·CK}/{CB} = {15 · 3√5 · 2}/{9√5} = 10$.
Задача 20
Периметр прямоугольника равен $28$, а площадь $48$. Найдите меньшую сторону прямоугольника.
Решение
Пусть $x$ и $y$ — две стороны прямоугольника. Из условия следует система уравнений:
$\{{\table {2(x+y)=28{,}}; {xy=48{.}};}$ Из первого уравнения системы: $x+y=14$; $y=14-x$. Подставляя выражение для переменной $y$ во второе уравнение системы, получим:
$x(14-x)=48$; $x^2-14x+48=0$; $x_1=8$, $x_2=6$. Тогда $y_1=14-8=6$, $y_2=14-6=8$. Следовательно, меньшая сторона прямоугольника равна $6$.
Рекомендуемые курсы подготовки

- 👻 Вспомнишь алгебраические преобразования
- 👻 Отработаешь линейные, квадратные и дробно-рациональные уравнения
- 👻 Покоришь движение по воде
- 👻 И в целом крайне продуктивно проведешь время
на бесплатном курсе Турбо ЕГЭ

