Задание 8. Функции. Производная и первообразная. ЕГЭ 2026 по математике профильного уровня
Средний процент выполнения: 76%
Ответом к заданию 8 по математике (профильной) может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 8:
Определить по условию, что требуется: касательная, производная, экстремум, наибольшее/наименьшее значение, площадь через интеграл.
Если требуется производная, найти производную функции (элементарной или составной, как задано).
Если требуется исследование функции, использовать производную для нахождения критических точек и анализа поведения функции на нужном промежутке.
Если требуется наибольшее/наименьшее значение на промежутке, вычислить значения функции в точках, которые следуют из исследования, и сравнить их.
Если требуется касательная, использовать найденные значения (точка касания/производная) для составления уравнения касательной.
Если требуется площадь фигуры, задать границы и вычислить интеграл согласно условию.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
На рисунке изображён график функции $y=f(x)$. Найдите среди точек $x_1, x_2, x_3, x_4, x_5, x_6$ те точки, в которых производная функции $f(x)$ равна нулю. В ответе запишите количество найденных точек.
Решение
Производная равна нулю в тех точках, где касательная горизонтальна. В частности, в точках максимума и минимума. По графику находим искомые точки: $x_1$, $x_3$, $x_5$, $x_6$, всего четыре (см. рис. $$).
Задача 2
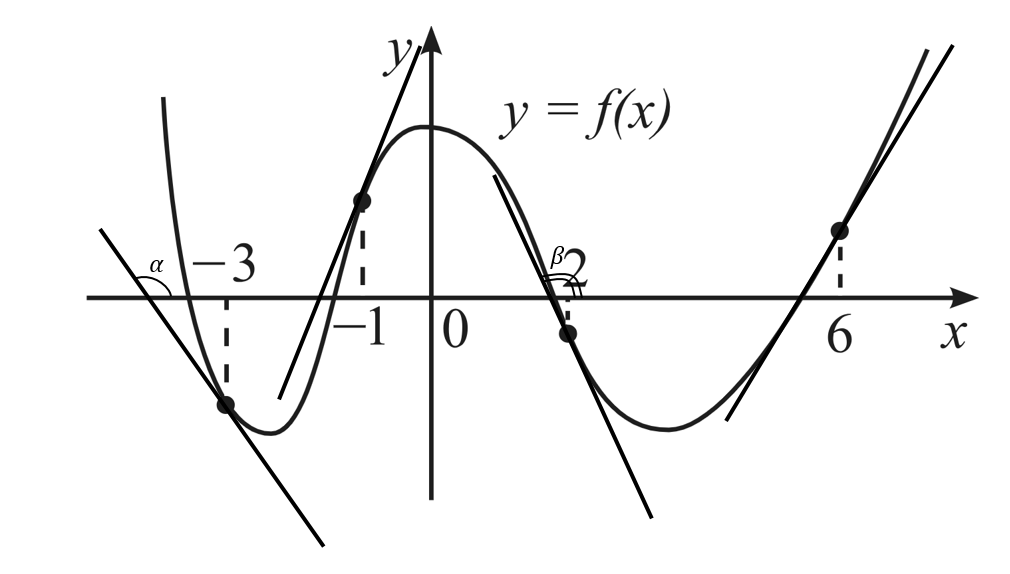
На рисунке изображён график функции $y=f(x)$ и отмечены точки $-3; -1; 2; 6$. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Решение
Значение производной в точке $x_0$ равно угловому коэффициенту касательной, проведённой к графику этой функции в точке с абсциссой $x_0$. $f'(x)$ наименьшее в точке, в которой касательная образует самый маленький тупой угол с осью $Ox$ («горка» в этом месте на вид «самая крутая»). Проведём касательные в заданных точках (см. рис.). Тупые углы (а значит, $f'(x)<0$) в точках $x=-3$ и $x=2$. $β<α$, значит, наименьшая производная в точке $2$.
Задача 3
На рисунке (см. с. ) изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-5; 7)$. В какой точке отрезка $[-3; 2]$ $f(x)$ принимает наименьшее значение?
Решение
На отрезке $[-3; 2]$ производная функции $y=f(x)$ отрицательна, значит, $f(x)$ убывает (см. рис. $$). Тогда наименьшее значение функция принимает при наибольшем значении аргумента, то есть в точке $2$.
Задача 4
На рисунке изображён график функции $y=f(x)$, определённой на интервале $(-7; 10)$. Найдите количество точек, в которых касательная к графику функции параллельна прямой $y=-3$ или совпадает с ней.
Решение
Угловой коэффициент касательной $y=-3$ равен нулю, следовательно, искомыми точками будут точки экстремума (см. рис. $$). Таких точек — девять.
Задача 5
На рисунке изображён график функции $y=f(x)$ и отмечены точки $-4; -1; 3; 6$. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Решение
Проводим касательные к графику в точках с указанными абсциссами (см. рис.).
Определяем, под каким углом $α$ они наклонены к положительному направлению оси $Ox$.
Согласно геометрическому смыслу производной $f'(x_0)=\tg α$, то есть значения тангенсов построенных углов — это и есть значения производной в указанных точках
Замечаем, в точках $-4$ и $3$ касательные наклонены под острым углом, поэтому в этих точках значение производной положительно.
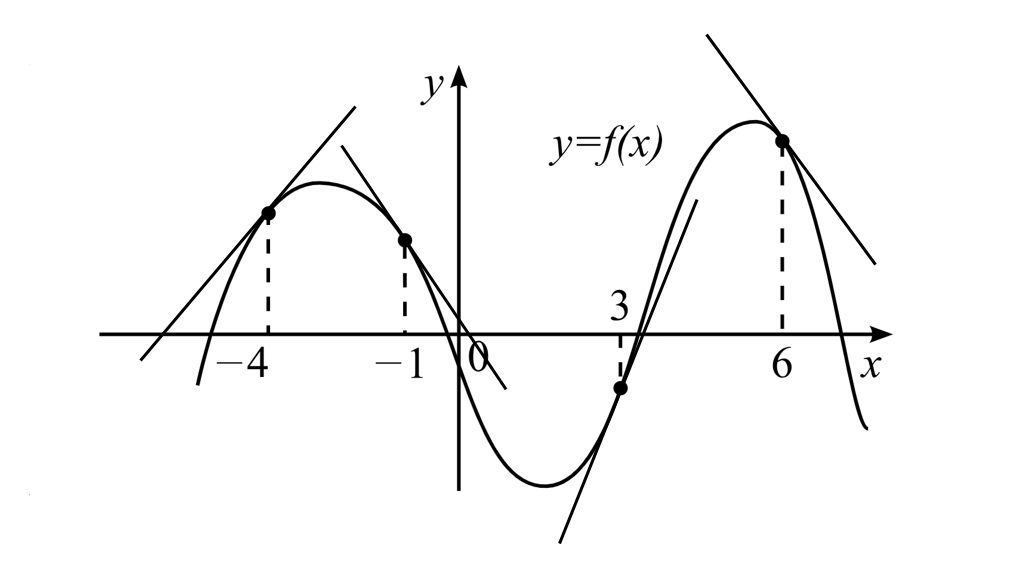
Учитывая, что касательная, проведённая к графику функции в точке с абсциссой $3$, образует больший угол с положительным направлении оси $Ox$, значит, значение производной в этой точке наибольшее.
Задача 6
На рисунке изображён график функции $y=F(x)$ — одной из первообразных функции $f(x)$, определённой на интервале $(-6; 7)$. Найдите количество решений уравнения $f(x)=0$ на отрезке $[-3; 4]$.
Решение
По определению первообразной на интервале $(-6; 7)$ $f(x)=F'(x)$. Следовательно, решениями уравнения $f(x)=0$ являются точки экстремума (см. рис. $$). На отрезке $[-3; 4]$ таких точек три: $A$, $B$, $C$. Значит, уравнение $f(x)=0$ имеет три решения.
Задача 7
На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке $x_0$. Уравнение касательной показано на рисунке. Найдите значение производной функции $g(x)=4f(x)-12$ в точке $x_0$.
Решение
Найдём производную функции $g(x)$, $g'(x)=(4f(x)-12)'=4⋅ f'(x)$. Найдём значение $f'(x_0)$. Значение производной в точке касания равно угловому коэффициенту касательной $f'(x_0)=(0{,}8x+4)'=0{,}8$. Тогда искомое значение $g'(x_0)=4⋅0{,}8=3{,}2$ (см. рис.)
Задача 8
Прямая $y=5x+4$ параллельна касательной к графику функции $y=x^2-4x-12$. Найдите абсциссу точки касания.
Решение
Значение производной в точке касания равно угловому коэффициенту касательной. Касательная параллельна прямой $y=5x+4$, значит, её угловой коэффициент равен: $(5x+4)'=5$. Абсциссу точки касания найдём из уравнения $(x^2-4x-12)'=5$, $2x-4=5$, $x=4{,}5$.
Задача 9
Материальная точка движется прямолинейно по закону
$x(t)={2} / {3}t^3-4t^2-12t$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени $t=6$ с.
Решение
Скорость материальной точки — это производная пути по времени $v(t)=x'(t)=({2} / {3}t^3-4t^2-12t)'={3⋅2} / {3}t^2-8t-12=2t^2-8t-12$. $v(6)=2⋅ 36-8⋅6-12=72-48-12=12$.
Задача 10
На рисунке изображён график функции $y=f(x)$. Найдите среди точек $x_1, x_2, x_3, x_4, x_5, x_6, x_7$ те точки, в которых производная функции $f(x)$ положительна. В ответе запишите количество найденных точек.
Решение
Производная положительна только в тех точках, которые принадлежат промежуткам возрастания функции. Таких точек $3: x_1, x_2, x_6$.
Задача 11
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-5; 8)$. Найдите количество точек, в которых касательная к графику функции $f(x)$ параллельна прямой $y=2x-4$ или совпадает с ней.
Решение
Значение производной в точке касания равно угловому коэффициенту касательной. Касательная параллельна прямой $y=2x-4$ или совпадает с ней, значит, её угловой коэффициент $k=(2x-4)'=2$ (см. рис. $$). Найдём количество точек, в которых $f'(x)=2$. Оно равно количеству точек пересечения графика $y=f'(x)$ с прямой $y=2$. Таких точек $3$.
Задача 12
На рисунке изображён график функции $y=f(x)$. Функция $F(x)=x^3-6x^2+14x+{1} / {2}$ — одна из первообразных функции $f(x)$. Найдите площадь заштрихованной фигуры.
Решение
Площадь заштрихованной фигуры равна разности значений первообразных, вычисленных в точках $3$ и $1$ (см. рис. $$). $F(1)=1-6+14+0{,}5=9{,}5$ $F(3)=3^3-6⋅3^2+14⋅3+0{,}5=15{,}5$ $F(3)-F(1)=15{,}5-9{,}5=6$.
Задача 13
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-7; 8)$. Найдите, в какой точке отрезка $[-4; 4]$ функция принимает наибольшее значение.
Решение
На отрезке $[-4; 4]$ $f'(x)=0$ в единственной точке $x=-2$. При переходе через эту точку производная меняет знак с плюса на минус (см. рис. ). Значит, $x=-2$ — точка максимума, следовательно, в ней функция принимает наибольшее значение на этом отрезке.
Задача 14
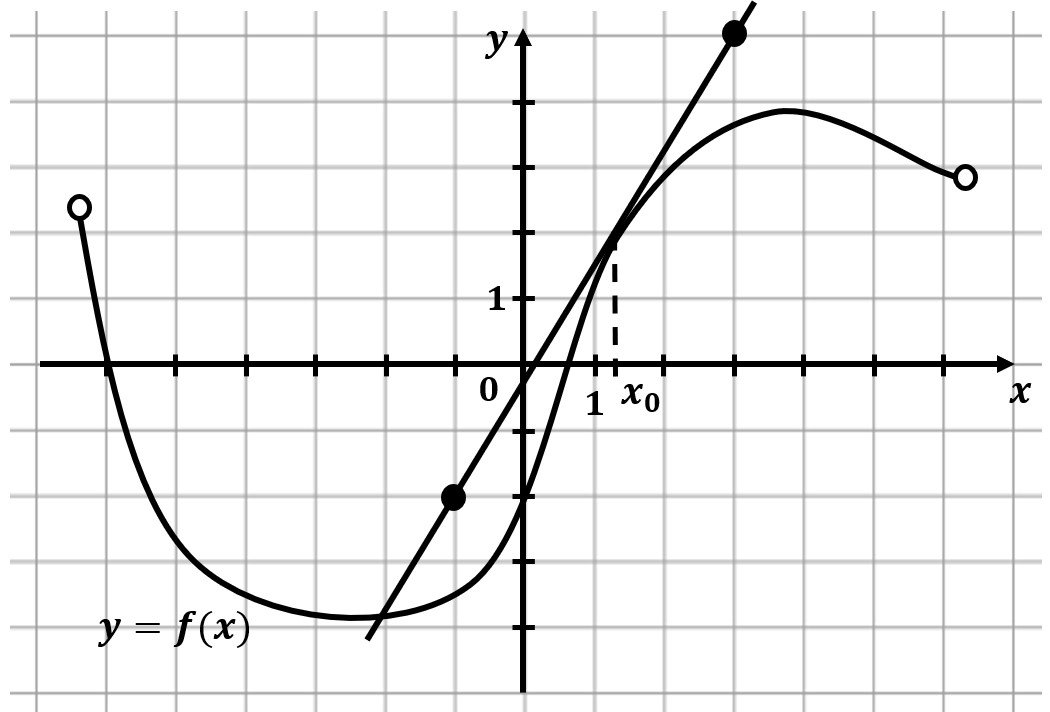
На рисунке изображены график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение
$f'(x_0)=tgα={7}/{4}=1,75;$
т.к. $α<90°$, то $tgα>0$
Если касательная в точке возрастает, то производная будет положительной
Задача 15
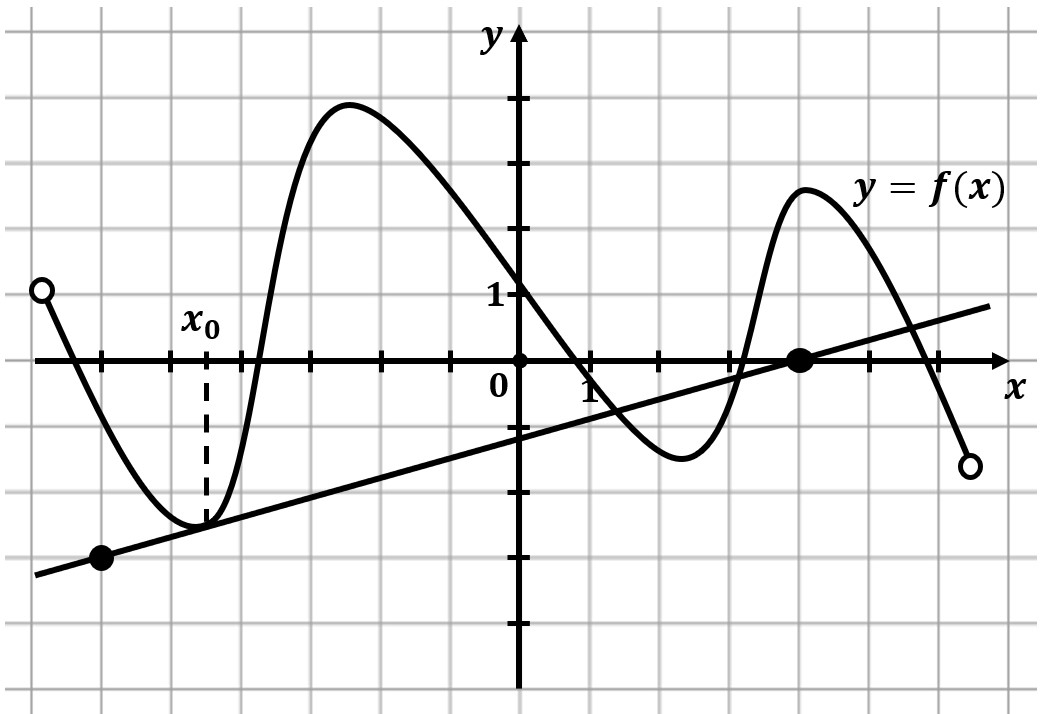
На рисунке изображены график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение
$f'(x_0)=tgα={3}/{10}=0,3;$
т.к. $α<90°$, то $tgα>0$
Если касательная в точке возрастает, то производная будет положительной
Задача 16
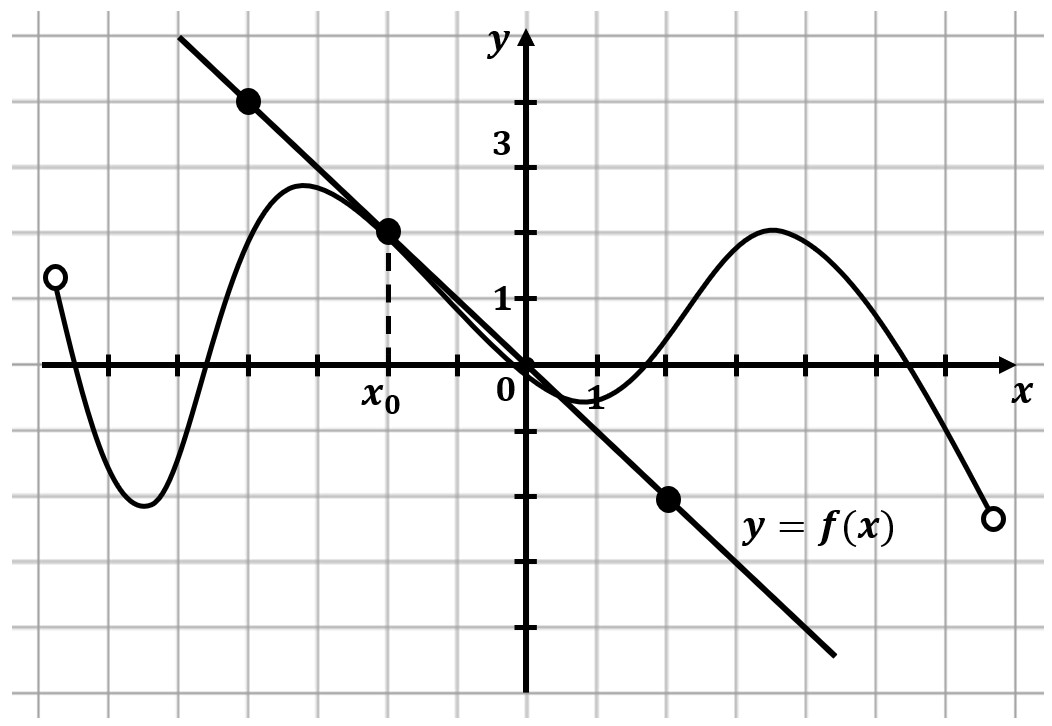
На рисунке изображены график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение
$f'(x_0)=tgα=-{6}/{6}=-1;$
т.к. $α>90°$, то $tgα<0$
Если касательная в точке убывает, то производная будет отрицательной
Задача 17
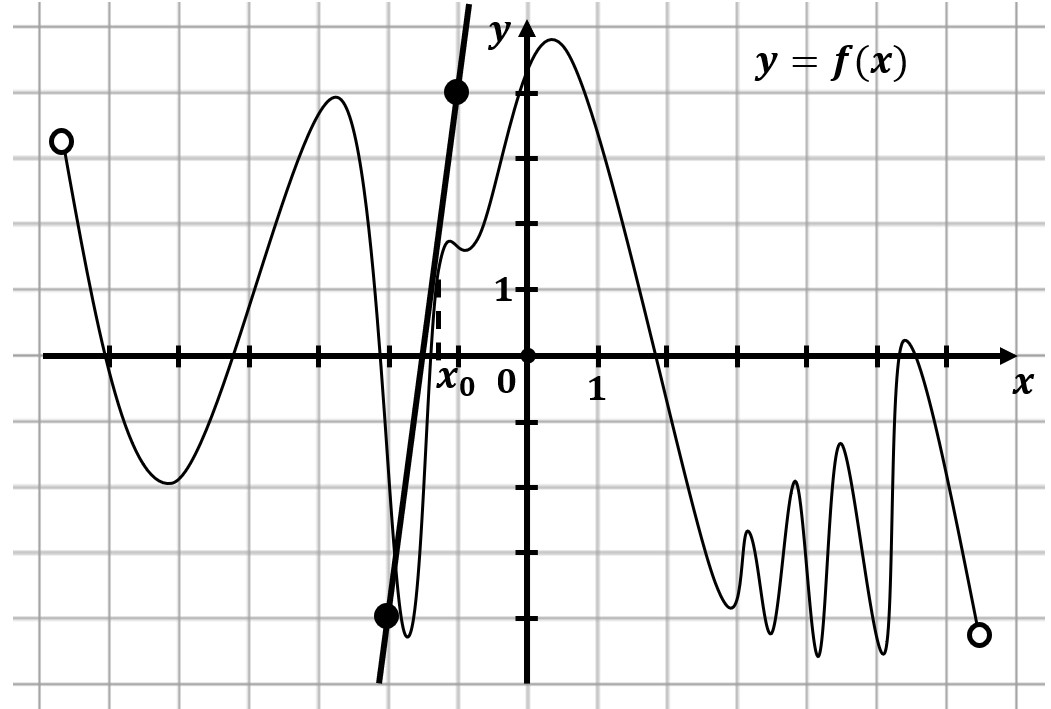
На рисунке изображены график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение
$f'(x_0)=tgα={8}/{1}=8;$
т.к. $α<90°$, то $tgα>0$
Если касательная в точке возрастает, то производная будет положительной
Задача 18
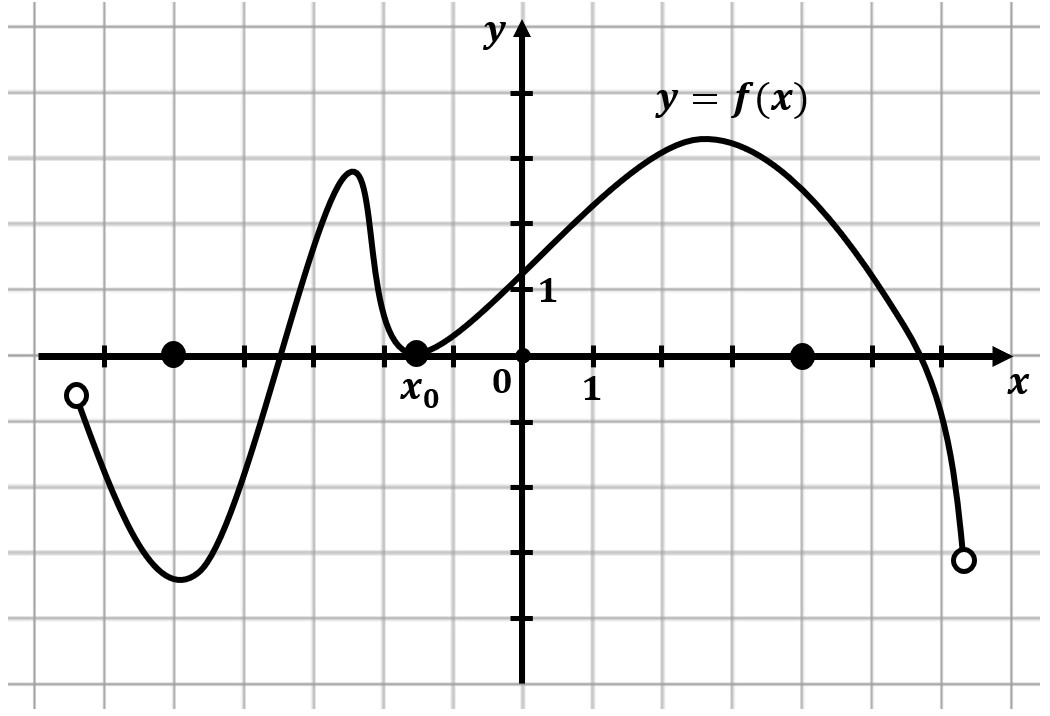
На рисунке изображены график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение
$f'(x_0)=tgα={0}/{9}=0;$
т.к. $α=180°$, то $tgα=0$
Касательная проходит через точку минимума, в точке касания она ни возрастает, ни убывает
Задача 19
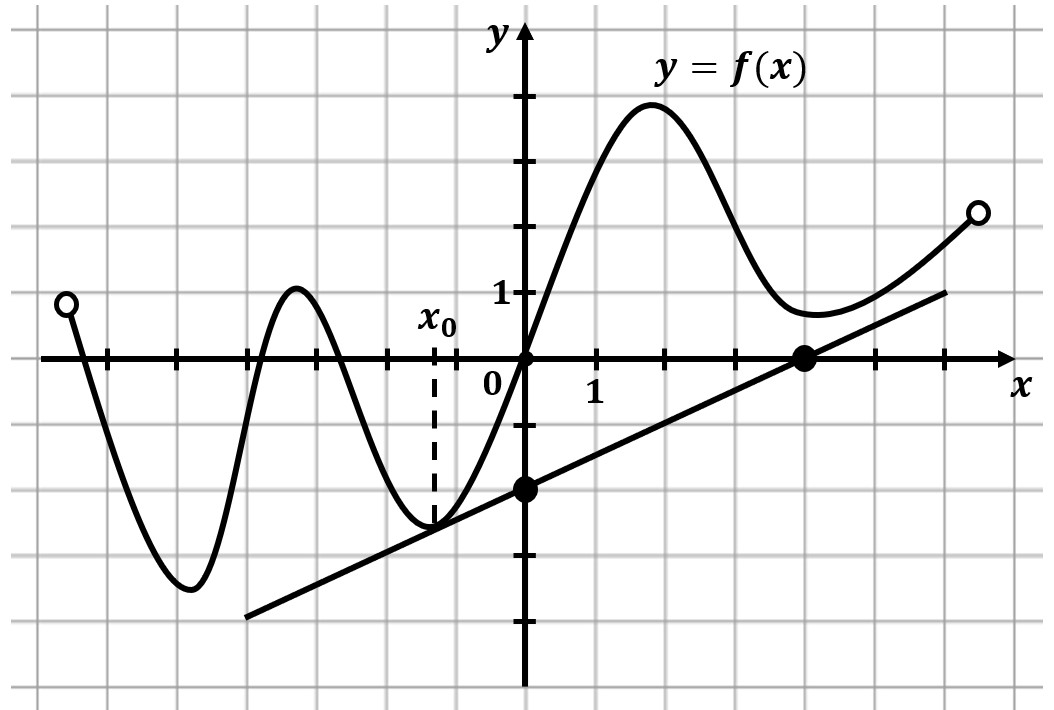
На рисунке изображены график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение
$f'(x_0)=tgα={2}/{4}=0,5;$
т.к. $α<90°$, то $tgα>0$
Если касательная в точке возрастает, то производная будет положительной
Задача 20
Прямая $y=891$ параллельна касательной к графику функции $y=x^2-26x+785$. Найдите абсциссу точки касания.
Решение
$y=891, y=x^2-26x+785$
$k_1=0, k_2=f'(x_0)$
$y'=2x-26; f'(x_0)=2x_0-26$
так как прямые параллельны, то угловые коэффициенты равны, тогда
$0=2x_0-26$
$2x_0=26$
$x_0=26:2$
$x_0=13$
Рекомендуемые курсы подготовки

- Узнаешь, как выглядят графики функций.
- Разберешься, как по данному графику определить, какая функция задана.
- Научишься решать все прототипы 11 задания профильной математики.
- Получишь море полезных материалов.
на бесплатном курсе Турбо ЕГЭ







