Статистика
Задание №13 является мостиком между 1 и 2 частями и от ее выполнения часто зависит, сможешь ли ты набрать выше 70 баллов, для многих это решающие баллы при получении золотой медали, так или иначе эти 2 первичных балла – фундамент для поступления, особенно на бюджет.
Алгоритм решения задания №13
- Находить ОДЗ — область допустимых значений переменной. Например, если мы видим в задаче √x, нужно отметить, что x⩾0. Также нужно быть аккуратным с логарифмами, знаменателем, tg(x) и ctg(x), которые существуют не при всех значениях переменной x.
- Хорошо знать тригонометрию. В 95% случаев на ЕГЭ дают либо чисто тригонометрическое уравнение, либо уравнение смешанного типа, в котором присутствует тригонометрия.
Что тебе точно пригодится: табличные значения, формулы приведения, знаки тригонометрических функций, решение простейших тригонометрических уравнений, формулы двойного аргумента, синус и косинус суммы (разности), основное тригонометрическое тождество. - Сделать замену. Большинство уравнений сводится к замене. Например, если перед тобой уравнение:
то удобнее сделать замену и продолжать решение для другой переменной, а затем вернуться к исходной. В данном примере необходимо написать:
Не забываем об ограничении на показательную функцию. То есть если у нас получится корень t=-5, то он нам не подойдет.
- Владеть представлением об ограничениях для стандартных функций. Как показал пример выше, необходимо проявить бдительность и знать ограничение на показательную функцию. А вот функция логарифма может принимать значения от минус бесконечности до плюс бесконечности. У нас есть ограничения на основания логарифма и на число, стоящее под логарифмом, но если мы заменяем логарифм, то на новую переменную никаких ограничений накладывать не будем.
- Отбирать полученные корни. Есть множество способов отбора и у каждого свои критерии. Сегодня в примере разберем самый распространенный способ — отбор окружностью
Пример
Как было отмечено ранее, сделаем замену и решим квадратное уравнение для новой переменной:
Оба корня получились неотрицательными, значит нам подойдут Сделаем обратную замену и найдем решения для исходной переменной:
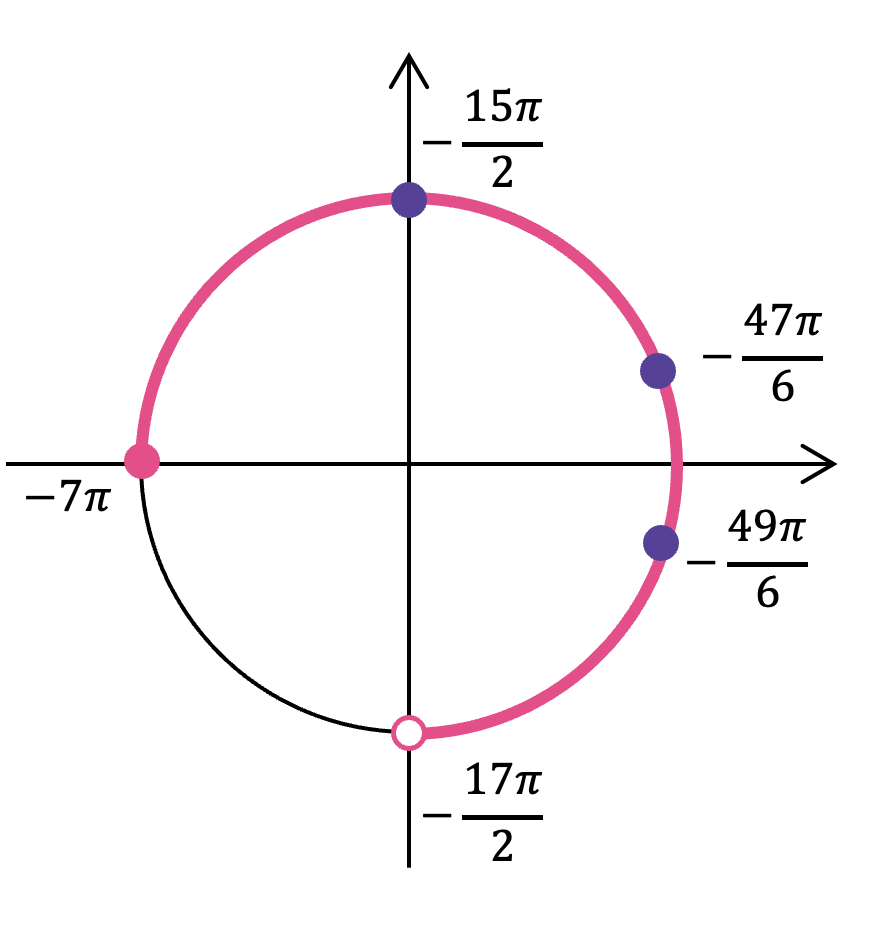
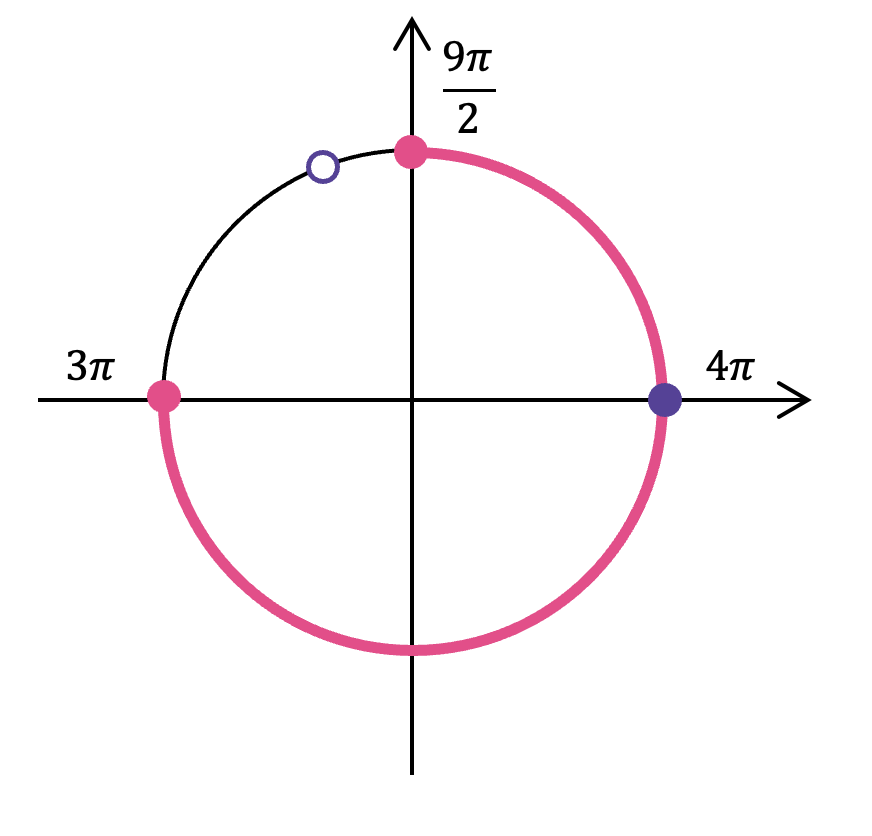
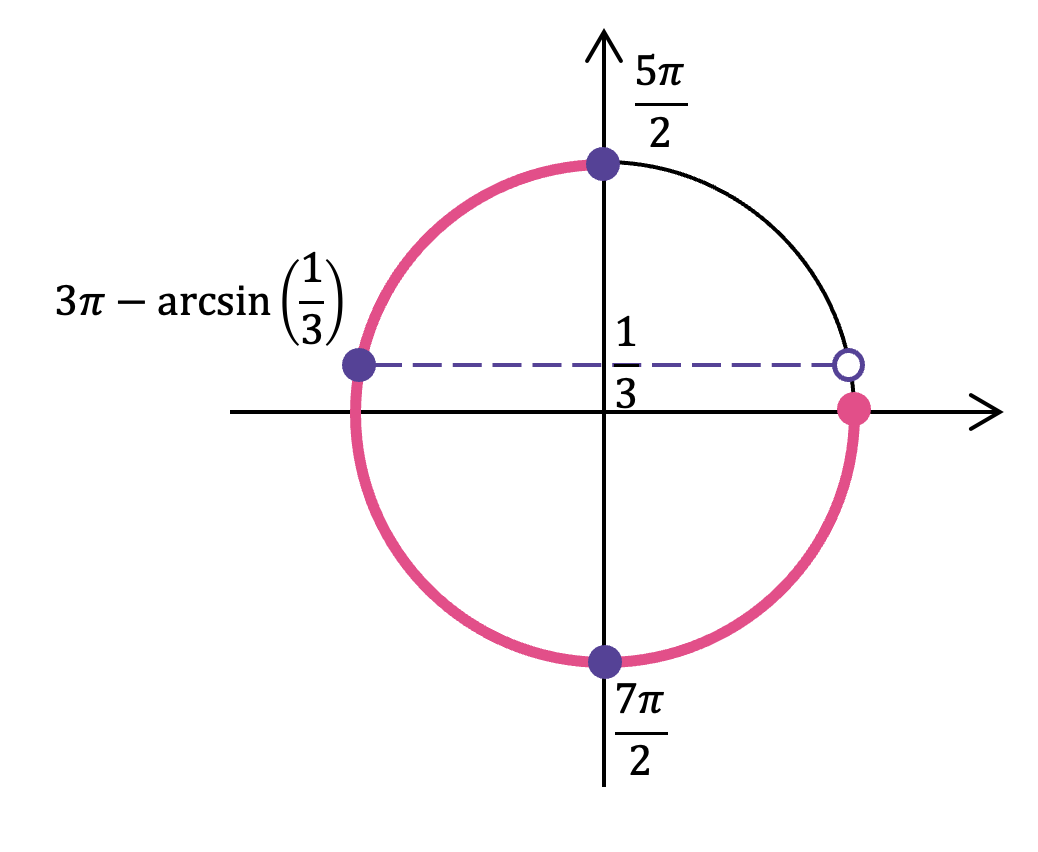
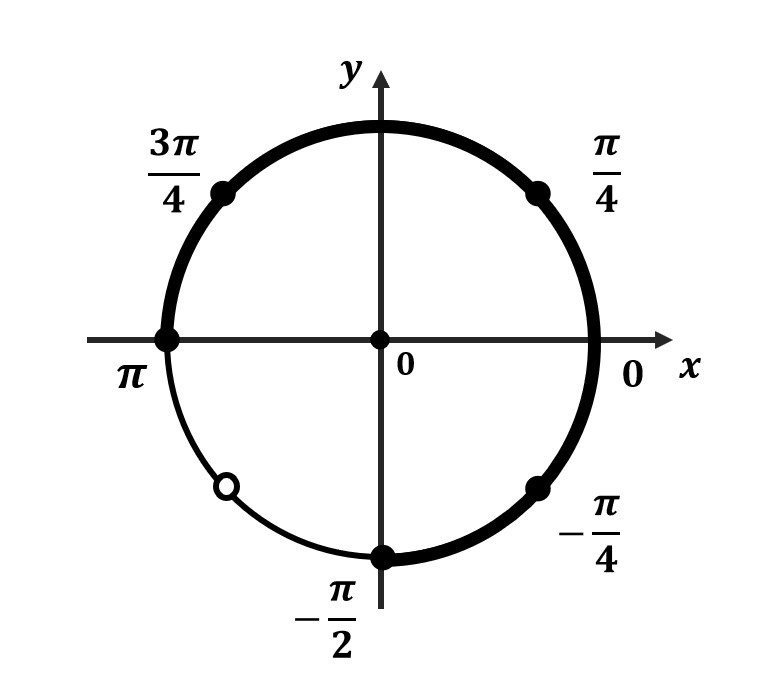
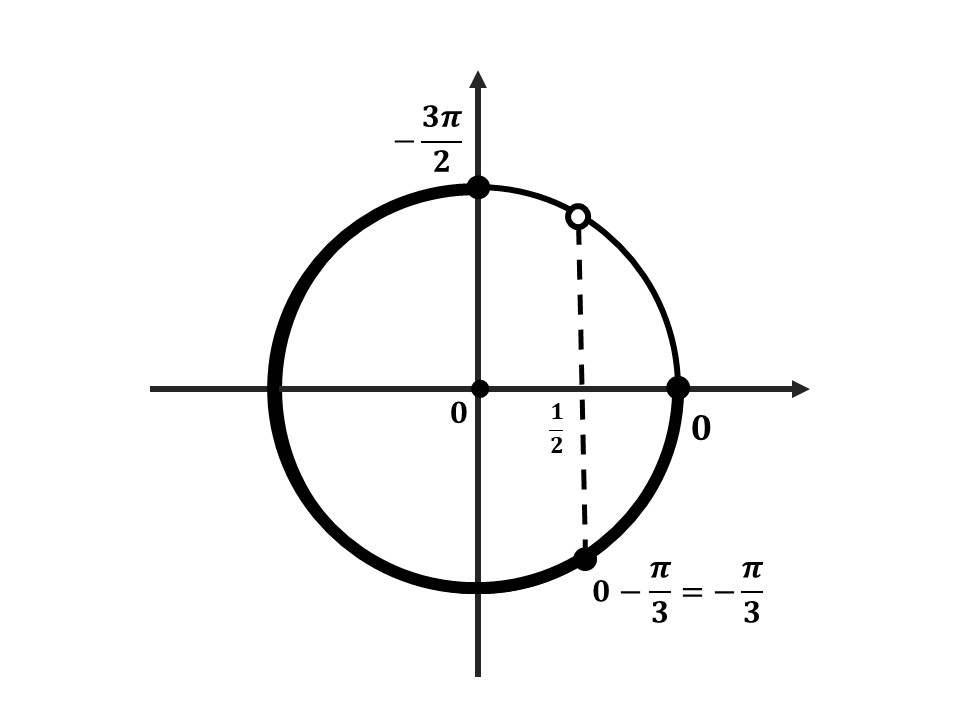
В пункте (а) рисовать окружность не обязательно, здесь она приведена только для вашего удобства. Вот мы и набрали 1 балл, теперь давайте воспользуемся способом отбора корней при помощи единичной окружности и заработаем максимальное количество баллов за задачу.
Давайте разберем критерии такого отбора. Это очень важно, потому что при их невыполнении эксперт может посчитать отбор недостаточно обоснованным:
Критерии отбора корней с помощью окружности
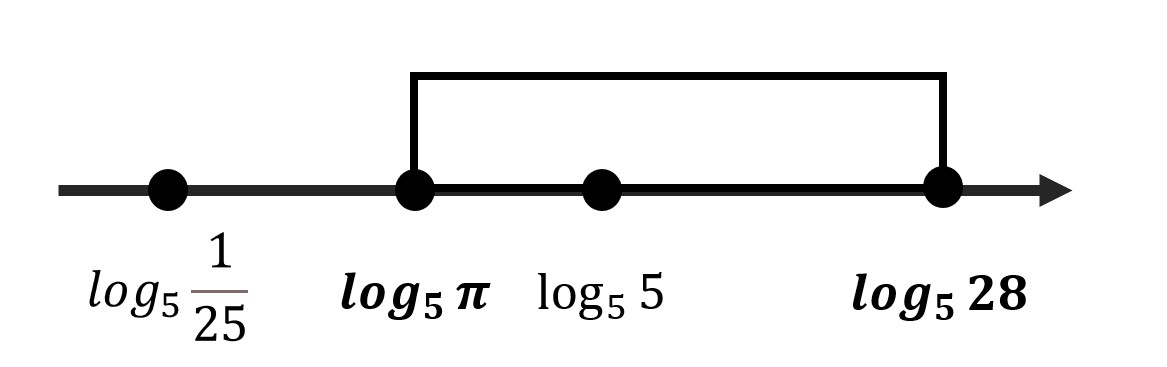
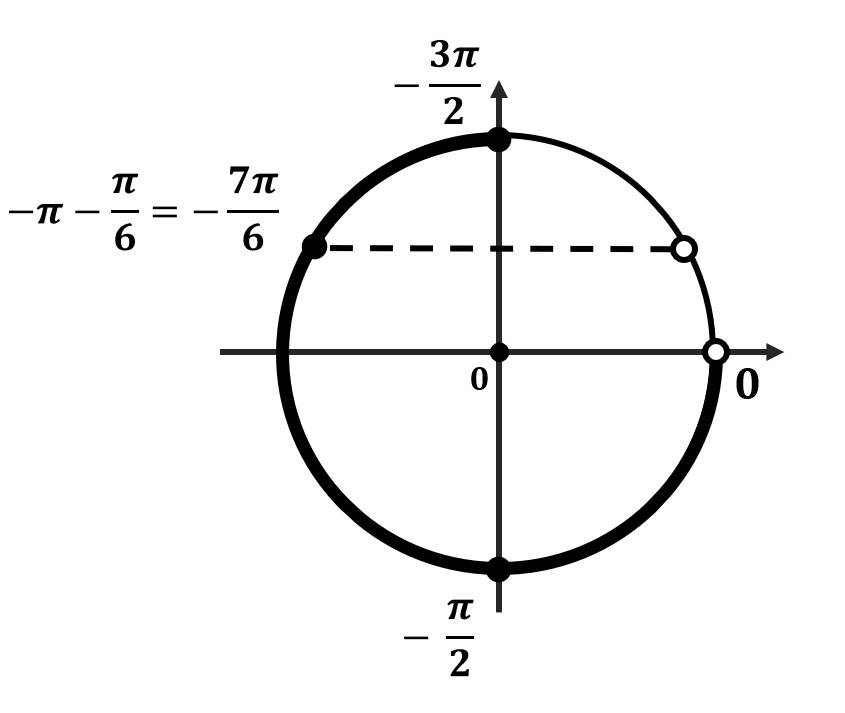
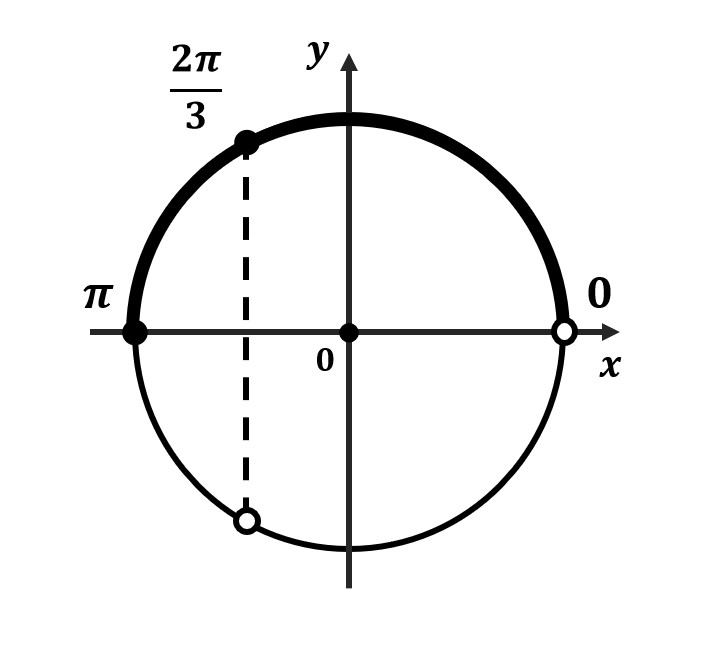
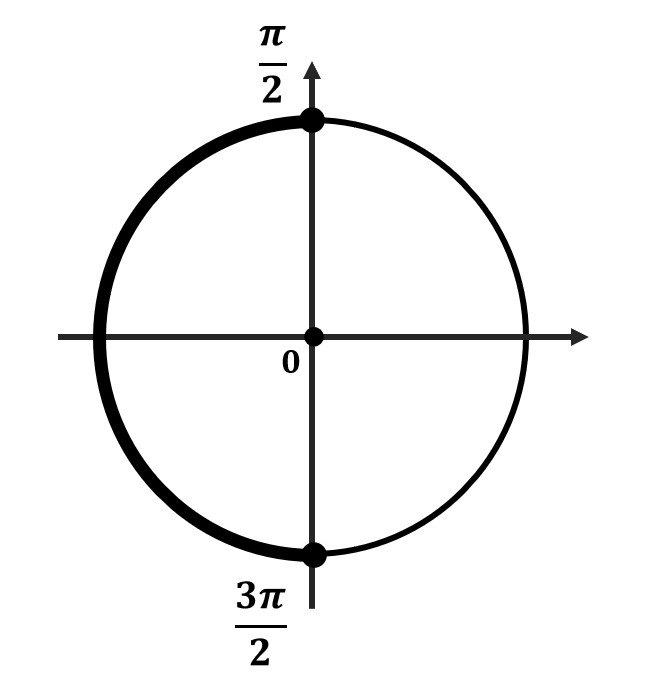
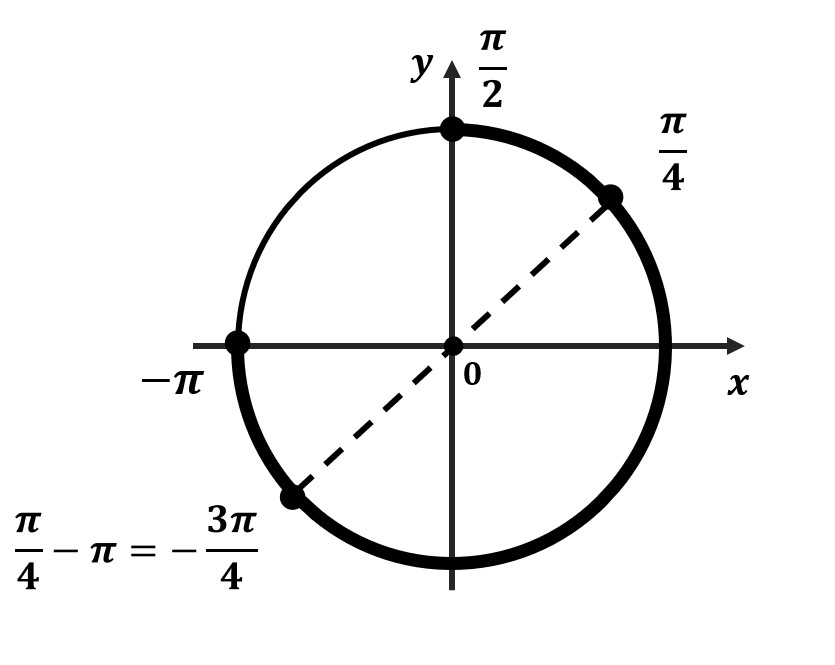
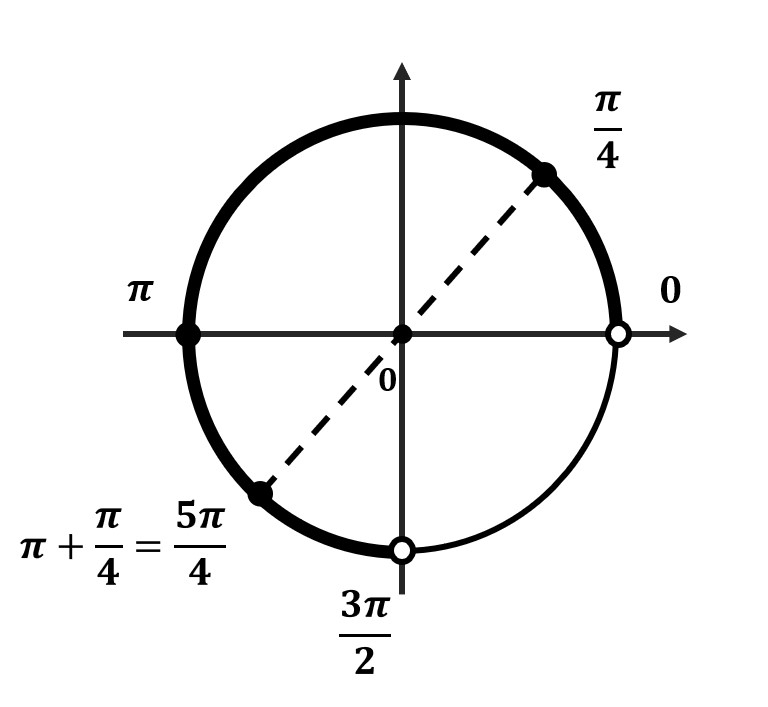
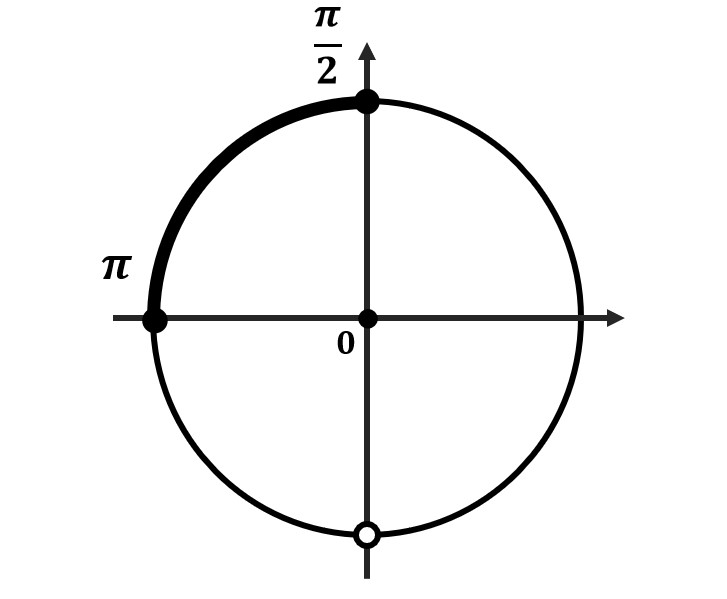
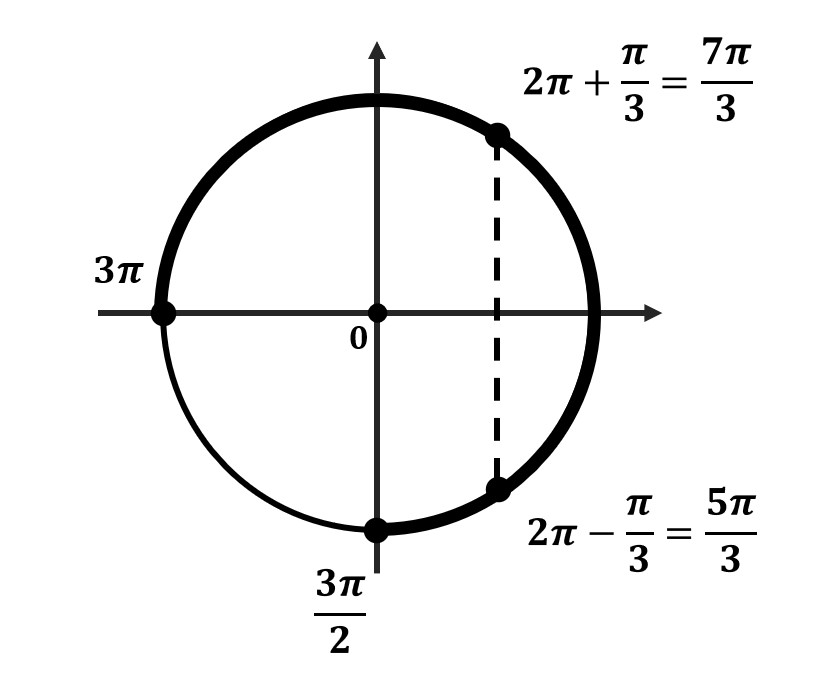
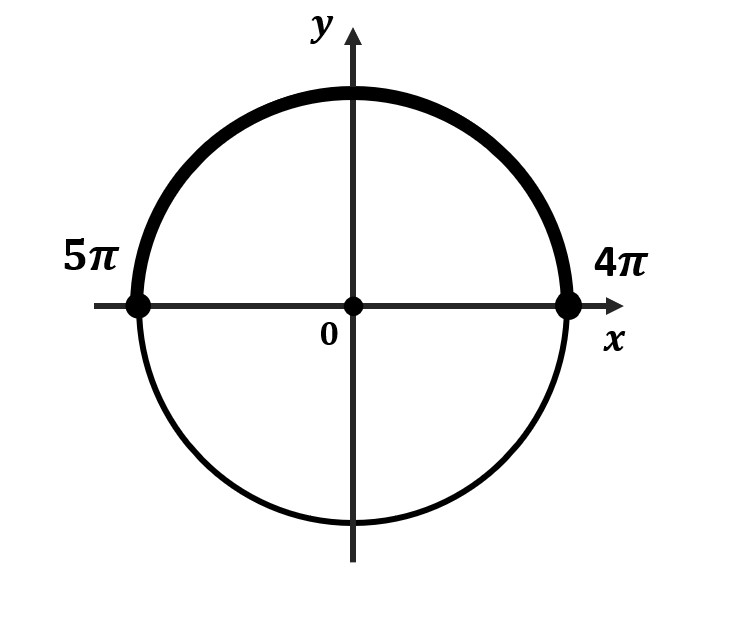
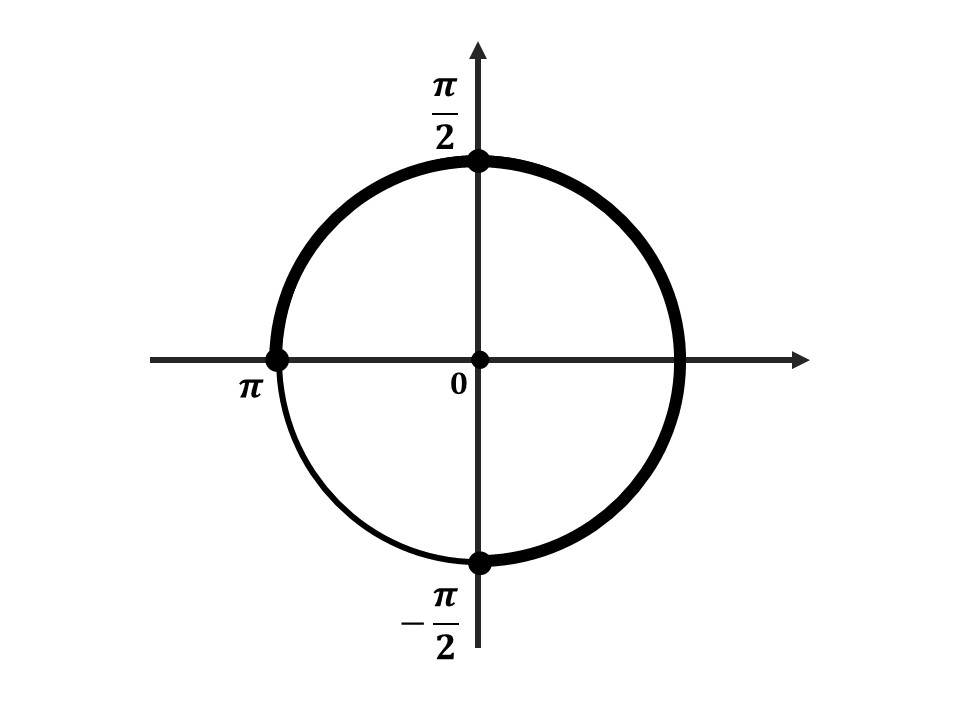
- Отметь на окружности граничные точки
- Заштрихуй область об меньшего значения к большему (против часовой стрелки)
- Отметь все подходящие корни на окружности и обязательно подпиши их значения. Желательно отдельно распиши, как ты их получил.
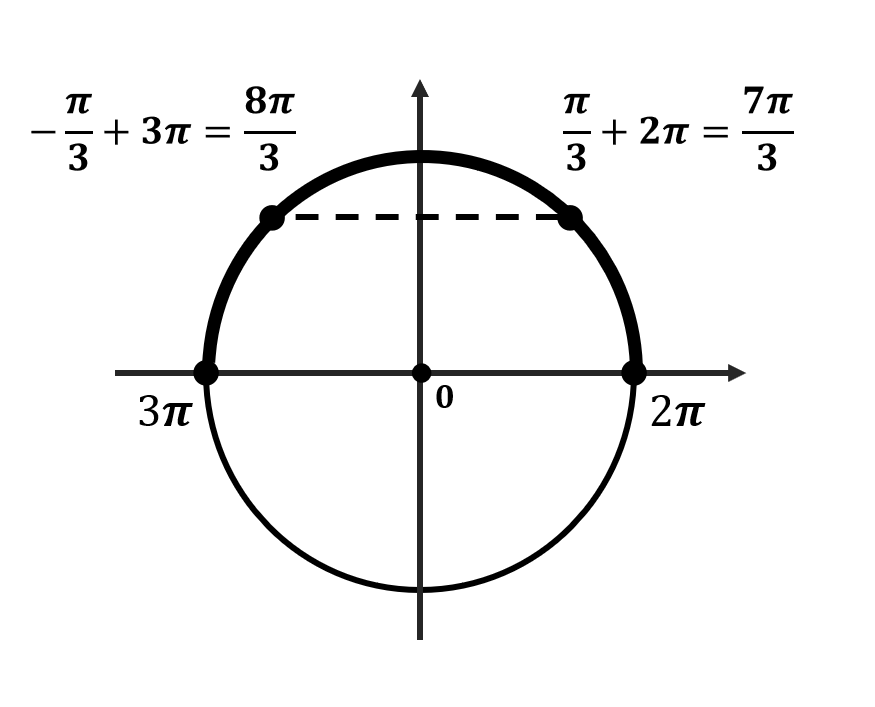
Вот тебе аналогичный пример для решения дома, потренируйся и я уверен, что практика задания 13 принесет тебе 2 балла на экзамене.
Еще больше крутых лайфхаков, разборов, ловушек ЕГЭ и теории в нашей группе вконтакте и инсте преподавателей @turboegemath и @turbomath
