Задание 14. Задача на стереометрию. ЕГЭ 2026 по математике профильного уровня
Средний процент выполнения: 6%
Ответом к заданию 14 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Алгоритм решения задания 14:
Прочитать условие и определить, какие геометрические объекты заданы и какие величины требуется найти.
Выполнить аккуратный чертёж, отразив взаимное расположение точек, прямых и плоскостей.
Выявить заданные отношения: параллельность, перпендикулярность, равенства углов или отрезков.
Определить, какие углы, расстояния или площади можно выразить через известные элементы.
Выбрать подходящие теоремы и свойства планиметрии или стереометрии для установления нужных соотношений.
Записать необходимые геометрические равенства или зависимости между величинами.
Выполнить вычисления, последовательно находя промежуточные и искомые значения.
Проверить, что полученный результат согласуется с геометрическим смыслом задачи и условиями.
Сформулировать ответ в виде требуемой геометрической величины.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
В правильной четырёхугольной пирамиде $SABCD$ сторона основания равна $8$, а боковое ребро $SA$ равно $2√ {33}$. На рёбрах $AB$ и $SB$ отмечены точки $K$ и $L$ соответственно, причём $AK=2$, $SL:LB=1:6$. Плоскость $α$ перпендикулярна плоскости $ABC$ и содержит точки $K$ и $L$. а) Докажите, что плоскость $α$ содержит точку $C$. б) Найдите площадь сечения пирамиды $SABCD$ плоскостью $α$.
Решение
а) $SO$ — высота пирамиды $SABCD$, $O$ — точка пересечения диагоналей квадрата $ABCD$ (см. рис.). В плоскости диагонального сечения $BSD$ проведём $LH∥ SO$, тогда $LH⊥ ABC$. Плоскость $HKL$ перпендикулярна плоскости $ABC$ по признаку перпендикулярности плоскостей и совпадает с плоскостью $α$. $▵ SOB∼▵ LHB$ как прямоугольные с общим острым углом $B$, тогда $OH:HB=SL:LB=1:6$, $OB={1} / {2}BD=4√ 2$, $OH={4√ 2} / {7}$, $HB={24√ 2} / {7}$. Из прямоугольного треугольника $BCK(∠ B=90°)$ по теореме Пифагора $CK=√ {BC^2+BK^2}=10$. Из прямоугольного треугольника $COH (∠ O=90°)$ по теореме Пифагора $CH=√ {CO^2+OH^2}=√ {32+{32} / {49}}={40} / {7}$. По теореме косинусов для треугольника $BHK$ $(∠ HBK=45°)$ $HK^2=BH^2+BK^2-2BH⋅ BK⋅{√ 2} / {2}$, $HK^2=({24√ 2} / {7})^2+36-2⋅{24√ 2} / {7}⋅6⋅{√ 2} / {2}={900} / {49}$, $HK={30} / {7}$. $CH+HK={40} / {7}+{30} / {7}=10=CK$, следовательно, точка $C$ принадлежит прямой $KH$, а значит, и плоскости $α$. б) Площадь сечения пирамиды $SABCD$ плоскостью $α$ равна площади треугольника $CKL$, основание которого $CK=10$, а высоту $LH$ найдём из подобия треугольников $SOB$ и $LHB$ (см. п. а). Высота $SO$ пирамиды — катет прямоугольного треугольника $SOB$. $SO=√ {SB^2-OB^2}=√ {132-32}=10$, тогда
$SO:LH=SB:BL=7:6$, $10:LH=7:6$, $LH={60} / {7}$. $S_{сеч}={1} / {2}⋅ CK⋅ LH={1} / {2}⋅10⋅{60} / {7}={300} / {7}$
Задача 2
Дана правильная треугольная пирамида $SABC$, $AB=18$. Высота $SO$, проведённая к основанию, равна 10, точка $M$ — середина $AS$, точка $K$ — середина $BC$. Плоскость, проходящая через точку $M$ и параллельная основанию пирамиды, пересекает рёбра $SB$ и $SC$ в точках $L$ и $N$ соответственно.
а) Докажите, что $LN$ проходит через середину отрезка $SK$.
б) Найдите угол между плоскостью основания и плоскостью $ALN$.
Решение
а) Плоскость $LMN$ по условию параллельна плоскости $ABC$ (см. рис.). Плоскость $ABS$ проходит через прямую $AB$, параллельную плоскости $LMN$ и пересекает её по прямой $ML$, значит, $ML∥ AB$, $ML$ — средняя линия треугольника $ABS$ и $L$ — середина ребра $BS$. Аналогично $LN∥ BC$, $LN$ — средняя линия треугольника $BCS$. $P$ — точка пересечения $LN$ и $SK$. Имеем $SL=LB$, $LP∥ BK$, тогда по теореме Фалеса $SP=PK$. б) Линия пересечения плоскостей $ALN$ и $ABC$ проходит через точку $A$ и параллельна $BC$ (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает её, то линия пересечения параллельна этой прямой). Боковые грани правильной пирамиды — равные равнобедренные треугольники, следовательно, $AL=AN$. В равнобедренном треугольнике $ALN$ $AP⊥ LN$. В правильном треугольнике $ABC$ $AK⊥ BC$. Это означает, что $∠ PAK$ — линейный угол искомого двугранного угла между плоскостью основания и плоскостью $ALN$. Проведём $PH⊥ ABC$, тогда $PH∥ SO$, $∠ PAK =∠ PAH$, $\tg∠ PAH={PH} / {AH}$. $P$ — середина отрезка $SK$ (см. п. а), $PH$ — средняя линия треугольника $OSK$, $PH={1} / {2} SO=5$, $OH={1} / {2} OK={1} / {2}⋅{1} / {3} AK={AK} / 6$, $AH=AO+OH={2AK} / 3+{AK} / 6={5AK} / 6={5} / {6}⋅ {AB√ 3} / 2= {15√ 3} / 2$. $\tg∠ PAH={5⋅ 2} / {15√ 3}={2√ 3} / 9$. $∠ PAH=\arctg{2√ 3} / 9$.
Задача 3
В основании прямой треугольной призмы $ABCA_1B_1C_1$ лежит равнобедренный треугольник $ABC$ с основанием $AC$. Точка $D$ — середина ребра $A_1B_1$, а точка $F$ делит ребро $AC$ в отношении $AF:FC=1:3$. a) Докажите, что $DF$ перпендикулярно $AC$. б) Найдите угол между прямой $DF$ и плоскостью $ABB_1$, если $AB=12$, $AC=8$ и $AA_1=10$.
Решение
а) Пусть $K$ — проекция точки $D$ на плоскость $ABC$, при этом $K$ — середина $AB$ (см. рис. $$). Пусть $H$ — середина $AC$. Тогда $BH⊥ AC$, так как треугольник $ABC$ — равнобедренный. Так как $AF={1} / {4} AC$ по условию и $AH={1} / {2} AC$, то $F$ — середина $AH$. Значит, $KF∥ BH$ как средняя линия треугольника $ABH$. Следовательно, $KF⊥ AC$. Поэтому $DF⊥ AC$ по теореме о трёх перпендикулярах. б) Проведём в плоскости $ABC$ $FL⊥ AB$, $FL⊥ AA_1$ ($AA_1⊥ ABC$), следовательно, $FL⊥ ABB_1$ и $DL$ — проекция $DF$ на плоскость $ABB_1$. Угол $FDL$ — это угол между прямой $DF$ и плоскостью $ABB_1$. $\sin∠ FDL={FL} / {FD}$. $▵ AFL∼▵ ABH$ как прямоугольные с общим острым углом $A$. Тогда ${FL} / {BH}={AF} / {AB}$. $AB=12$, $AH={1} / {2} AC=4$,
$BH=√ {AB^2-AH^2}=8√ 2$, $AF={1} / {4}AC=2$,
$FL={BH⋅ AF} / {AB}={8√ 2⋅ 2} / {12}={4√ 2} / {3}$, $DK=AA_1=10$, $FK$ — средняя линия треугольника $ABH$, $FK={1} / {2}BH=4√ 2$. По теореме Пифагора для треугольника $DFK$ $DF=√ {DK^2+FK^2}=√ {100+32}=2√ {33}$. $\sin∠ FDL={{4√ 2} / {3}} / {2√ {33}}={2√ {66}} / {99}$, $∠ FDL=\arcsin{2√ {66}} / {99}$.
Задача 4
В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ известны длины рёбер $AA_1=3√ 2$, $AB=3$, $AD=8$. Точка $K$ делит отрезок $A_1D_1$ в отношении $3:1$, считая от вершины $A_1$. а) Докажите, что плоскость, проходящая через точку $C$ перпендикулярно прямой $BK$, делит отрезок $B_1K$ в отношении $2:1$, считая от вершины $B_1$. б) Найдите косинус угла между этой плоскостью и плоскостью $BCC_1$.
Решение
а) Введём прямоугольную систему координат, как это показано на рисунке. Найдём координаты точек $A(0; 0; 0)$, $A_1(0; 0; 3√ 2)$, $B(3; 0; 0)$, $B_1(3; 0; 3√ 2)$, $D(0; 8; 0)$, $K(0; 6; 3√ 2)$ Плоскость $α$, проходящая через точку $C$ перпендикулярно прямой $BK$, имеет вектор нормали ${{BK}↖{→}}\{-3; 6; 3√ 2\}$. Уравнение плоскости $α$ принимает вид $-3x+6y+3√ 2z+d=0$. Точка $C(3; 8; 0)$ принадлежит плоскости $α$. Подставим её координаты в полученное уравнение и найдём $-9+48+d=0$, $d=-39$. Итак, уравнение плоскости $α:-3x+6y+3√ 2z-39=0$. Отметим на прямой $B_1K$ точку $E(x; y; 3√ 2)$, тогда получаем ${{B_1K}↖{→}}\{-3; 6; 0\}$ и ${{B_1E}↖{→}}\{x-3; y; 0\}$. Так как ${{B_1K}↖{→}}$ и ${{B_1E}↖{→}}$ — сонаправленные векторы, то ${{B_1E}↖{→}}=t⋅ {{B_1K}↖{→}}$, ($t>0$), или в координатной форме $x-3=-3t$, $x=-3t+3$; $y=6t$. Координаты точки $E(-3t+3; 6t; 3√ 2)$. Если точка $E$ лежит в плоскости $α$, то подставляем координаты точки $E$ в уравнение плоскости $α$: $9t-9+36t+18-39=0$; $45t=30$; $t={2} / {3}$. Значит, $B_1E:B_1K=2:3$. Пусть $B_1E=2x$, $B_1K=3x$, тогда ${B_1E} / {EK}={B_1E} / {B_1K-B_1E}={2x} / {3x-2x}=2$. Следовательно, плоскость $α$ пересекает отрезок $B_1K$ и делит его в отношении $2:1$, считая от вершины $B_1$. б) Плоскость $α$ имеет вектор нормали ${{n}↖{→}}_1={{BK}↖{→}}\{-3; 6; 3√ 2\}$. Так как ось $Ax$ перпендикулярна плоскости $BCC_1$, то вектор нормали плоскости $BCC_1$ имеет координаты ${{n}↖{→}}_2={{AB}↖{→}}\{3; 0; 0\}$. Вычислим косинус искомого угла $\cos∠(α, BCC_1)={|{{n}↖{→}}_1⋅ {{n}↖{→}}_2|} / {|{{n}↖{→}}_1|⋅|{{n}↖{→}}_2|}={|-3⋅3+6⋅0+3√ 2⋅0|} / {√ {9+36+18}⋅√ {9+0+0}}={√ 7} / {7}$.
Задача 5
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ сторона $AB=AA_{1}=3$, $AD=6$. На рёбрах $AD$ и $CC_{1}$ взяты соответственно точки $M$ и $N$ — середины этих рёбер.
а) Постройте сечение параллелепипеда плоскостью, проходящей через вершину $D$, параллельно $MN$ и $B_{1}C$.
б) Найдите объём пирамиды, основание которой — построенное сечение, а вершина — точка $D_{1}$.
Решение
а) Искомое сечение проходит через вершину $D$ параллельно $B_1 C$, следовательно, пересекает грань $AA_1 D_1 D$ по диагонали $A_1 D$
Действительно, $A_1 D||B_1 C$ (плоскость пересекает две параллельные плоскости по параллельным прямым)
Рассмотрим прямоугольник $C C_1 M_1M$, где $M_1$ середина $A_1 D_1$
Проведём $C_1 K ||M N$. $K$ — середина отрезка $M M_1$ и середина отрезка $A_1 D$, значит, принадлежит искомому сечению, поэтому $C_1 K$ лежит в плоскости сечения
Таким образом, $A_1 C_1 D$ — искомое сечение.
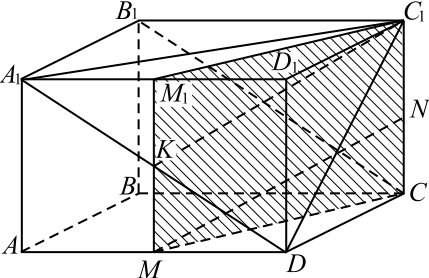
б) Рассмотрим пирамиду $D_1A_1C_1D$ как пирамиду с основанием $D_1DC_1$ и высотой $A_1D_1 (A_1D_1 ⊥ D_1DC_1)$.
$V_{D_1A_1C_1D} = {1}/{3}S_{D_1DC_1} ·A_1D_1 = {1}/{3} · {1}/{2}D_1C_1 ·D_1D ·A_1D_1 = {1}/{6} ·3·3·6 = 9$.
Задача 6
Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали граней $AA_1B_1B$ и $BB_1C_1C$ равны $2√ {41}$ и $10$ соответственно, $AB=10$.
а) Докажите, что треугольник $A_1C_1B$ прямоугольный.
б) Найдите объём пирамиды $ACC_1B_1$.
Решение
а) Так как $A_1C_1 ⊥ B_1C_1$ и $A_1C_1 ⊥ CC_1$ по условию, то $A_1C_1 ⊥ BB_1C_1$ по признаку перпендикулярности прямой и плоскости.

Следовательно, $A_1C_1 ⊥ BC_1$, то есть треугольник $A_1C_1B$ прямоугольный.
б) 1) $AC = A_1C_1 = √{A_1B^2 - BC^2_1} = √{(2√{41})^2 - 10^2} = 8$.
2) $B_1C_1 = BC = √{AB^2 - AC^2} = √{10^2 - 8^2} = 6$.
3) $CC_1 = √{BC_1^2 - BC^2} = √{10^2 - 6^2} = 8$.
4) $V_{ACC_1B_1} = {1}/{3}·S_{ACC_1} ·B_1C_1 = {1}/{3} · {1}/{2} ·AC·CC_1 ·B_1C_1 = {1}/{6} ·8·8·6 = 64$.
Задача 7
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=3$, $BC=5$, $CD=4$, а высота пирамиды $PABCD$ равна $7$.
Решение
а) 1) $∠AKD = 180° - (∠A + ∠D) = 180° - 90° = 90°$.
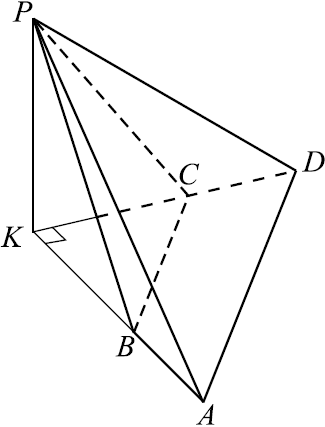
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, также перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ - линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) Обозначим $BK = x, CK = y$.
1) $△BKC∼ △AKD$, так как $AD ‖ BC$.
Тогда ${AK}/{BK} = {DK}/{CK}; {AB + BK}/{BK} = {CD + CK}/{CK}; {AB}/{BK} + 1 = {CD}/{CK} + 1; {AB}/{BK} = {CD}/{CK}; {3}/{x} = {4}/{y}; x = {3}/{4}y$.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; x^2 + y^2=5^2; ({3}/{4}y)^2+y^2=25; {25}/{16}y^2=25; y=4;x={3}/{4}y=3$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}·3 ·4= 6$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·6·7 = 14$.
Задача 8
На боковом ребре $FD$ правильной четырёхугольной пирамиды ${FABCD}$ отмечена точка $M$ так, что $FM:FD=1:3$. Точки $P$и $Q$ — середины рёбер $AD$ и $BC$ соответственно.
а) Докажите, что сечение пирамиды плоскостью $MPQ$ есть равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость $MPQ$ разбивает пирамиду.
Решение
а) 1) Построим $MN ‖ CD$.
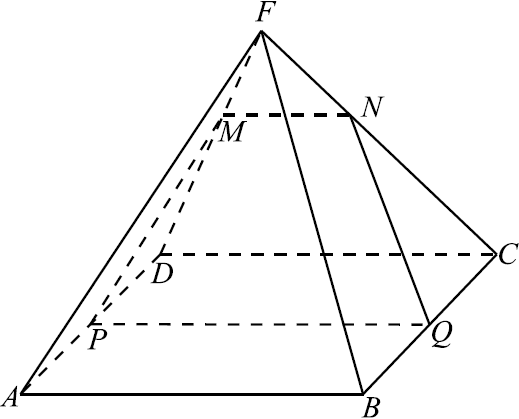
Так как и $PQ ‖ CD$, то $MN ‖ PQ$. Следовательно, точки $M, N, P$ и $Q$ лежат в одной плоскости. Таким образом, трапеция $MNQP$ является сечением пирамиды плоскостью $MPQ$.
2) $△FMN ∼△FDC$ (так как $MN ‖ CD$, то $∠FNM = ∠FCD$ и $∠FMN = ∠FDC$ как соответственные). Так как $△FCD$ равнобедренный, то и $△FNM$ тоже равнобедренный. Тогда $FM = FN; NC = FC - FN = FD - FM = MD$.
Кроме того, $PD = {1}/{2}AD = {1}/{2}BC = QC$. Так как $△FAD = △FBC$, то $∠MDP = ∠NCQ$. Отсюда $△PDM = △QCN$ по двум сторонам и углу между ними. Следовательно, $PM = NQ$, то есть $MNQP$ - равнобедренная трапеция.
б) 1) Пусть $MR ⊥ PQ, MS ⊥ CD, NX ⊥ PQ, NY ⊥ CD$.

Так как $MNQP$ и $MNCD$ - равнобедренные трапеции, то $V_1 = V_{PQCDMN} = V_{MRSNXY} + 2·V_{NXQCY}$ - объём первой части.
2) Пусть $a$ - сторона основания, $h$ - высота пирамиды. Тогда $QC = XY = RS = {a}/{2}; MN = {1}/{3}a; MO = {2}/{3}h(△FMN ∼△FDC$ и ${FM}/{FD} = {1}/{3}; QX = {PQ -MN}/{2} = {a -{1}/{3}a}/{2} = {1}/{3}a (MNQP$ - равнобедренная трапеция).
3) $S_{MRS} = {1}/{2}RS·MO = {1}/{2}·{a}/{2}·{2}/{3}h = {1}/{6}ah$. Объём прямой призмы $MRSNXY$ равен $V_{MRSNXY} = S_{MRS}·MN = {1}/{6}ah·{1}/{3}a = {1}/{18}a^2h$.
$V_{NXQCY} = {1}/{3}S_{XQCY}·MO = {1}/{3}·QX·QC·MO = {1}/{3}·{1}/{3}a·{a}/{2}·{2}/{3}h = {1}/{27}a^2h$.
$V_1 = V_{MRSNXY} + 2·V_{NXQCY} = {1}/{18}a^2h + 2·{1}/{27}a^2h = {7}/{54}a^2h$.
4) $V = V_{SABCD} = {1}/{3}S_{ABCD}·h = {1}/{3}a^2h$.
$V_2 = V - V_1 = ({1}/{3} - {7}/{54})a^2h = {11}/{54}a^2h$ - объём второй части.
5) ${V_1}/{V_2} ={{7}/{54}a^2h}/{{11}/{54}a^2h} = {7}/{11}$.
Задача 9
Дана четырёхугольная пирамида $SABCD$ с прямоугольником $ABCD$ в основании, $AB=6$, $BC=6√ {2}$. Высота пирамиды проектируется в точку пересечения диагоналей основания. Из вершин $A$ и $C$ на ребро $SB$ опущены перпендикуляры $AP$ и $CQ$.
а) Докажите, что точка $P$ является серединой отрезка $BQ$.
б) Найдите угол между плоскостями $SBA$ и $SBC$, если $SD=12$.
Решение
а) Пусть боковое ребро $SB$ равно $x$.
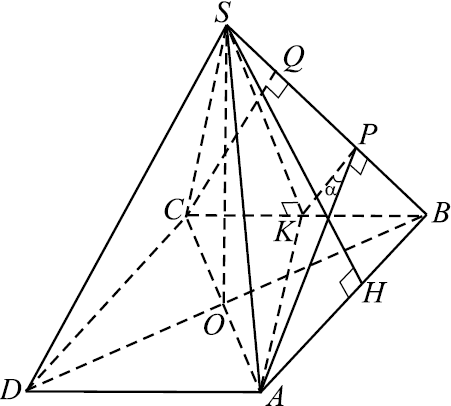
1) $△SHB∼△APB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${PB}/{BH} = {AB}/{SB}$. $H$ - середина $AB$. Тогда ${PB}/{3} = {6}/{x}; PB = {18}/{x}$.
2) $△SKB∼△CQB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${QB}/{BK} = {BC}/{SB}; {QB}/{3√2} = {6√2}/{x}; QB = {36}/{x}$.
3) Так как ${QB}/{PB} = {{36}/{x}}/{{18}/{x}} = 2$, то $PQ = PB$.
б) 1) Из пункта а) следует, что $PK$ - средняя линия $△BCQ$. Следовательно, $PK ‖ QC$. Но так как $QC ⊥ BS$, то и $PK ⊥ BS$. Значит, $∠APK$ - линейный угол двугранного угла между гранями $SBA$ и $SBC$. Пусть, $∠APK = α$.
2) $AK = √{AB^2 + BK^2} = √{6^2 + (3√2)^2} = 3√6$.
3) Так как по условию $SD = 12$ и $SB = SD$ (равным проекциям соответствуют равные наклонные), то $x = 12$, а $QB = {36}/{x} = {36}/{12}=3$.
Тогда $CQ = √{BC^2 - QB^2} = √{(6√2)^2 - 3^2} = 3√7$.
Так как $PK$ - средняя линия, то $PK = {1}/{2}CQ = {3√7}/{2}$.
4) $PB = {1}/{2}QB = {1}/{2}·3 = {3}/{2}$.
$AP = √{AB^2 - PB^2} = √{6^2 - ({3}/{2})^2} = {3}/{2}√{15}$.
5) По теореме косинусов для $△APK$:
$AK^2 = AP^2 + PK^2 - 2·AP·PK·cosα$;
$54 = {135}/{4} + {63}/{4} - 2·{3}/{2}√{15}·{3√7}/{2}·cosα$;
$cosα = - {1}/{√{105}}$;
Так как $cosα < 0$, то $α$ - тупой угол.
Значит, искомый угол между плоскостями $SBA$ и $SBC$ равен ($π-α$).
$cos(π-α) = -cosα = {1}/{√{105}}$.
Следовательно, искомый угол равен $arccos{1}/{√{105}}$.
Задача 10
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=BC=CD=4$, а высота пирамиды $PABCD$ равна $9$.
Решение
а) 1) $∠AKD = 180° - (∠A + ∠D) = 180° - 90° = 90°$.
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, так же перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ - линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) 1) Так как $ABCD$ - равнобедренная трапеция, то $∠A = ∠D$. Так как $BC ‖ AD$, то $∠A = ∠KBC, ∠D = ∠KCB$ как соответственные. Значит, $∠KBC = ∠KCB$, то есть $△KBC$ равнобедренный.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; 2BK^2 = BC^2; BK^2 = {BC^2}/{2} = {4^2}/{2} = 8$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}BK^2 = {1}/{2}·8 = 4$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·4·9 = 12$.
Задача 11
Основанием прямой треугольной призмы $PQRP_1Q_1R_1$ является прямоугольный треугольник $PQR$ с прямым углом $R$. Диагонали боковых граней $PP_1Q_1Q$ и $PP_1R_1R$ равны $17$ и $15$ соответственно, $PQ = 10$.
а) Докажите, что треугольник $P_1QR$ прямоугольный.
б) Найдите объём пирамиды $P_1QRR_1$.
Решение
По условию задачи сделаем чертёж.
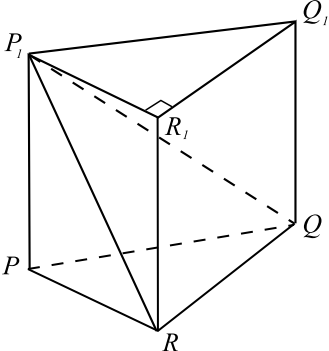
а) Прямая $QR$ перпендикулярна плоскости $PP_1R_1R$, поскольку она перпендикулярна прямым $PR$ и $RR_1$. Значит, прямые $QR$ и $RP_1$ перпендикулярны, следовательно, в $△P_1QR$
$∠P_1RQ = 90°$.б) Пусть $V$ — объём призмы $PQRP_1Q_1R_1$. Тогда объём треугольной пирамиды $PP_1QR$ равен ${V}/{3}$, поскольку её высота $PP_1$ и основание $PQR$ совпадают с высотой и основанием призмы соответственно. Аналогично, объём треугольной пирамиды $P_1Q_1R_1Q$ равен ${V}/{3}$. Призма $PQRP_1Q_1R_1$ составлена из трёх пирамид: $PP_1QR, P_1Q_1R_1Q$ и $P_1QRR_1$. Значит, объём пирамиды $P_1QRR_1$ равен ${V}/{3}$.
В призме $PQRP_1Q_1R_1 : QQ_1 = √{P_1Q^2 - P_1Q_1^2} = 3√21, QR = √{P_1Q^2 - P_1R^2} = 8, PR = √{PQ^2 - QR^2} = 6, V = PP_1 · {PR · QR}/{2} = 72√21$.
Таким образом, объём пирамиды $P_1QRR_1$ равен $24√21$.
Задача 12
Дана правильная четырёхугольная пирамида $SMNPQ$ с вершиной в точке $S$, сторона основания равна $7$, а плоский угол при вершине пирамиды равен $90°$.
а) Постройте сечение пирамиды плоскостью, проходящей через диагональ $NQ$ основания параллельно боковому ребру $PS$.
б) Найдите площадь сечения.
Решение
а) $PM$ пересекается с $NQ$ в точке $O$, при этом $O$ - середина $PM$ и $NQ$. В плоскости $MSP$ проведём $AO ‖ SP$, она пересечёт $SM$ в середине ребра ($OA$ - средняя линия $∆PSM$). Точку $A$ соединим с точкой $N$, $AN$ лежит в плоскости $MSN$, точку $A$ соединим с точкой $Q$, $AQ$ лежит в плоскости $MSQ$. В плоскости $ANQ$ находится прямая $AO ‖ PS$, и по признаку параллельности прямой и плоскости получаем: $PS ‖ ANQ$. Плоскость $ANQ$ содержит диагональ $NQ$ и параллельна боковому ребру $PS$, то есть сечение $NAQ$ является искомым.
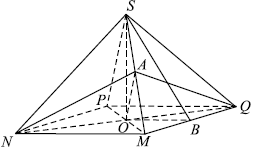
б) Докажем, что $∆ANQ$ - равнобедренный, то есть $AN = AQ$. Это следует из равенства треугольников $NAM$ и $AMQ$ (по двум сторонам: $MA$ - общая, $NM = MQ$ и углу: $∠AMQ = ∠AMN$).
$NQ = 7√2$ как диагональ квадрата со стороной $NM = 7$. Проведём $SB ⊥ MQ$.
В $∆BSM: ∠SMB = 45° (∠QSM = 90°; ∆QSM$ - равнобедренный), $∠BSM = 45°, SB = MB = {7}/{2}$. $MS = {MB}/{sin 45°} = {7}/{√2}$. Точка $O$ - середина $NQ, AO ‖ SP, AO$ - средняя линия $∆MSP, AO = {1}/{2} SP$. $AO = {7}/{2√2} = {7√2}/{4}. AO$ - высота $∆ANQ$, следовательно, $S_{сечения} = S_{∆ANQ} ={1}/{2}NQ·AO = {1}/{2}·7√2·{7√2}/{4} = {49·2}/{8} = {49}/{4} = 12.25$.
Задача 13
В основании пирамиды $ABCD$ лежит правильный треугольник $ABC$. Все боковые рёбра наклонены к основанию под одним и тем же углом.
а) Докажите, что $AB ⊥ CD$.
б) Найдите расстояние между прямыми $AB$ и $CD$, если $AB = 8√3, AD = 5√3$.
Решение
а) Рассмотрим рисунок.
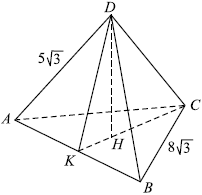
Так как все боковые рёбра наклонены под одним и тем же углом к основанию, то основание высоты пирамиды (это точка $H$) является центром окружности, описанной около треугольника $ABC$. Но треугольник $ABC$ - правильный, поэтому $H$ является точкой пересечения высот (а значит, и медиан). Отсюда следует, что $AB ⊥ CK$. По условию боковые рёбра пирамиды равны, поэтому треугольник $ABD$ равнобедренный, $DK$ является его медианой, значит, и высотой. Значит, $AB ⊥ DK$. Получаем, что $AB$ перпендикулярна двум пересекающимся прямым, лежащим в плоскости $KDC$, поэтому $AB ⊥ KDC$.
Следовательно, $AB ⊥ CD$.
б) Проведём в треугольнике $KDC$ высоту $KT$. Так как $AB ⊥ KDC$, то $AB ⊥ KT$. Значит, $KT$ является общим перпендикуляром к прямым $AB$ и $CD$, а длина отрезка $KT$ является расстоянием между прямыми $AB$ и $CD$.
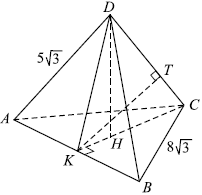
В равностороннем треугольнике $ABC$ высота $KC = AC·cos 30° = 8√3 ·{√3}/{2} = 12, KH = {1}/{3} KC = 4$. В треугольнике $ADK$ $AK = {1}/{2} AB = 4√3, KD = √{AD^2 - AK^2} = √{(5√3)^2 - (4√3)^2} = 3√3$.
В прямоугольном треугольнике $DHK$ $DH = √{KD^2 - KH^2} = √{27 - 16} = √{11}$.
$2 · S_{KDC} = KC · DH = KT · DC, KT = {KC · DH}/{DC} = {12 · √{11}}/{5√3} = {4√{33}}/{5}$.
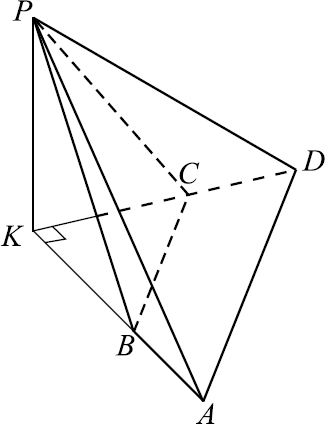
Задача 14
В правильной треугольной пирамиде $DABC$ с основанием $ABC$ сторона основания равна $6√3$, а высота пирамиды равна $8$. На рёбрах $AB, AC$ и $AD$ соответственно отмечены точки $M, N$ и $K$, такие, что $AM = AN = {3√3}/{2}$ и $AK = {5}/{2}$.
а) Докажите, что плоскости $MNK$ и $DBC$ параллельны.
б) Найдите расстояние от точки $K$ до плоскости $DBC$.
Решение
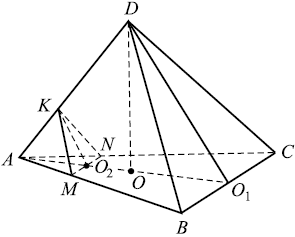
а) Плоскости $MNK$ и $DBC$ параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Докажем это. Рассмотрим прямые $MN$ и $KM$ плоскости $MNK$ и прямые $BC$ и $DB$ плоскости $DBC$.
В $∆AOD:∠AOD = 90°$ и по теореме Пифагора $AD = √{DO^2 + AO^2}$. Найдём $AO$, используя то, что $∆ABC$ правильный. $AO ={2}/{3} AO_1$, где $AO_1$ - высота $∆ABC, AO_1 = {a√3}/{2}$, где $a$ - сторона $∆ABC. AO_1 = {6√3· √3}/{2}= 9$, тогда $AO = 6, AD = √{8^2 + 6^2} = 10$.
1. Так как ${AK}/{AD} ={5}/{2} : 10 ={1}/{4}, {AM}/{AB} = {3√3}/{2} : 6√3 ={1}/{4}$ и $∠DAB$ - общий, то $∆AKM~∆ADB$. Из подобия следует, что $∠AKM = ∠ADB$. Это соответственные углы при прямых $KM$ и $BD$ и секущей $AD$. Значит, $KM ‖ BD$.
2. Так как ${AN}/{AC} = {3√3}/{2·6√3} ={1}/{4}, {AM}/{AB} ={1}/{4}$ и $∠CAB$ - общий, то $∆ANM~∆ACB$. Из подобия следует, что $∠ANM = ∠ACB$. Эти углы соответственные при прямых $MN$ и $BC$ и секущей $AC$. Значит, $MN ‖ BC$.
Вывод: так как две пересекающиеся прямые $KM$ и $MN$ плоскости $MNK$ соответственно параллельны двум пересекающимся прямым $BD$ и $BC$ плоскости $DBC$, то эти плоскости параллельны - $MNK ‖ DBC$.
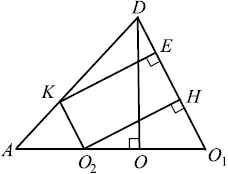
б) Найдём расстояние от точки $K$ до плоскости $BDC$. Поскольку плоскость $MNK$ параллельна плоскости $DBC$, то расстояние от точки $K$ до плоскости $DBC$ равно расстоянию от точки $O_2$ до плоскости $DBC$ и оно равно длине отрезка $O_2H$. Докажем это.
$BC ⊥ AO_1$ и $BC ⊥ DO_1$ (как высоты треугольников $ABC$ и $DBC$), значит, $BC$ перпендикулярна плоскости $ADO_1$, и тогда $BC$ перпендикулярна любой прямой этой плоскости, например $O_2H$. По построению $O_2H ⊥ DO_1$, значит, $O_2H$ перпендикулярна двум пересекающимся прямым плоскости $BCD$, и тогда отрезок $O_2H$ перпендикулярен плоскости $BCD$ и равен расстоянию от $O_2$ до плоскости $BCD$.
В треугольнике $O_2HO_1: O_2H = O_2O_1 sin∠HO_1O_2$.
$O_2O_1 = AO_1 - AO_2. {AO_2}/{AO_1} ={1}/{4}; AO_2 ={AO_1}/{4} ={9}/{4}$.
$O_2O_1 = 9 -{9}/{4} ={27}/{4}$.
$sin∠DO_1A ={DO}/{DO_1} ={8}/{√{64 + 3^2}} ={8}/{√{73}}$.
$O_2H ={27}/{4}·{8}/{√{73}} ={54}/{√{73}}$.
Задача 15
В правильной четырёхугольной призме $MNPQM_{1}N_{1}P_{1}Q_{1}$ сторона основания равна 11, а боковое ребро равно 15. На рёбрах $M_{1}Q_{1}, M_{1}N_{1}$ и $PQ$ взяты точки $X, Y , Z$, соответственно так, что $Q_{1}X = N_{1}Y = QZ = 5$.
а) Пусть $C$ - точка пересечения плоскости $XYZ$ с ребром $PN$. Докажите, что $XYZC$ - ] прямоугольник.
б) Найдите площадь сечения призмы плоскостью $XYZ$.
Решение
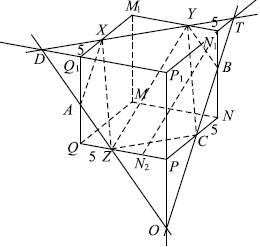
а) Найдём положение точки $C$. Эта точка пересечения плоскости $XYZ$ и ребра $PN$, лежащего в плоскости $MNPQ$. Плоскость $MNPQ$ параллельна плоскости $M_1N_1P_1Q_1$, в которой лежит отрезок $XY$. Плоскость $XYZ$ пересекает параллельные плоскости $MNPQ$ и $M_1N_1P_1Q_1$ по параллельным прямым, отсюда $XY ‖ ZC$. Прямоугольные треугольники $YXM_1$ и $ZCP$ равны по катету и острому углу ($M_1Y = PZ = 6$ и $∠M_1YX = ∠PZC$ как острые с соответственно параллельными сторонами).
Чтобы доказать, что четырёхугольник $XYCZ$ - прямоугольник, найдём длины его сторон и диагонали.
$XY = ZC = √{XM_1^2 +M_1Y^2} = √{36 + 36} = 6√2$,
$CY = XZ = √{ZQ^2 + QQ_1^2 + Q_1X^2} = √{25 + 225 + 25} = √{275} = 5√{11}$. Противоположные стороны четырёхугольника попарно равны, значит, это параллелограмм. Проведём $N_1N_2 ‖ YZ$, тогда $ZY = N_1N_2 = √{(ZP - YN_1)^2 + PN^2 + NN_1^2} = √{(PC - Q_1X)^2 + PQ^2 + QQ_1^} = CX$.
Диагонали параллелограмма равны, следовательно, $FKLP$ - прямоугольник.
б) Пусть $D$ и $T$ - точки пересечения прямой $XY$ и прямых $Q_1P_1$ и $P_1N_1$. Проведём прямые $DZ$ и $TC$, они пересекут рёбра $QQ_1$ и $NN_1$ в точках $A$ и $B$ соответственно. $D$ - точка пересечения прямых $XY$ и $AZ$. Тогда $DQ_1 = Q_1X = QZ$. Легко доказать, что треугольники $DQ_1A$ и $ZQA$ равны и $AQ = AQ_1$. Поэтому прямая $DZ$, а значит, и плоскость $XYZ$ пересекают ребро $QQ_1$ в его середине - точке $A$. Аналогично плоскость $XYZ$ пересекает ребро $NN_1$ в его середине - точке $B$.
В диагональном сечении $QQ_1N_1N$, которое является прямоугольником, отрезок $AB$ - средняя линия. В прямоугольнике $QABN$ противоположные стороны равны: $AB = QN = 11√2$.
Сечение $XY BCZA$ состоит из двух равных трапеций $AXYB$ и $AZCB$, причём мы доказали, что $ZX ⊥ XY$ и $ZX ⊥ ZC$. Высота каждой из этих трапеций равна ${ZX}/{2} ={5√{11}}/{2}$.
$S_{сечения}=2S_{AXYB}= 2·{AB + XY}/{2}·{XZ}/{2} = (11√2 + 6√2)·{5√{11}}/{2} = {85√{22}}/{2}$.
Рекомендуемые курсы подготовки

- Узнаешь, как выглядят графики функций.
- Разберешься, как по данному графику определить, какая функция задана.
- Научишься решать все прототипы 11 задания профильной математики.
- Получишь море полезных материалов.
на бесплатном курсе Турбо ЕГЭ







