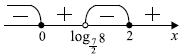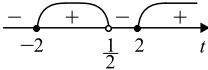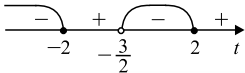В задании №15 требуется решить один из видов неравенств:

• Рациональное неравенство
• Показательное неравенство
• Логарифмическое неравенство, возможно с переменным основанием
• Неравенство с радикалом
• Смешанное неравенство, которое может содержать несколько видов одновременно

Получить за решение этого задания можно 2 первичных балла. Потерять 1 балл можно при вычислительной ошибке, при условии что имеется верная последовательность всех шагов решения.

Статистика выполнения задания №15 по годам

Метод интервалов

1. Решить уравнение f(x) = 0. Так мы найдем нули функции, от которых зависит знак неравенства. Удобно отдельно находить нули числителя и нули знаменателя.
2. Отметить все полученные корни (нули) на координатной прямой. Получим несколько интервалов.
3. Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) очень большое число, например, 1 000 000.
4. Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется. НО есть одно исключение:
   При переходе через нуль мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная.

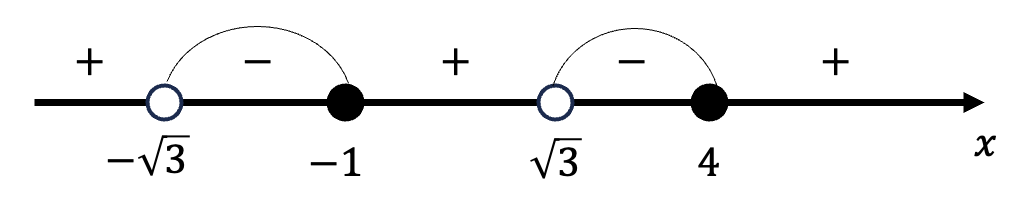
Пример 1

При переходе через нуль мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная.

Пример 2

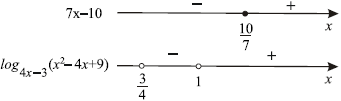
В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) = 0;

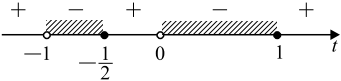
Пример 3

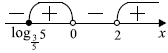
Знак правого промежутка был «+». Единственный нуль четной степени x = 10, поэтому в этом нуле знак не меняем. В остальных нулях чередуем знак.

Пример неравенства №15

Оформление задачи №15

Еще больше крутых лайфхаков, разборов, ловушек ЕГЭ и теории в нашей группе вконтакте и инсте преподавателей @turboegemath и @turbomath