$y'=-e^{x-3}+(4-x)e^{x-3}=e^{x-3}(-1+4-x)=(3-x)e^{x-3}$. $y'=0$ при $x=3$. Знак производной $y'$ совпадает со знаком выражения $3-x$. Наибольшее значение на отрезке $[1; 9]$ функция принимает в точке максимума, то есть при $x=3$ (см. рис. ). $y(3)=(4-3)e^{3-3}=1$.

$y'=-e^{5-x}-(5-x)e^{5-x}=e^{5-x}(-1-5+x)=(x-6)e^{5-x}$. $y'=0$ при $x=6$, $y'<0$ при $x<6$, $y'>0$ при $x>6$. При переходе через точку $x=6$ производная меняет знак с минуса на плюс, следовательно, $x=6$ — точка минимума функции.

Функция $y(x)$ определена, непрерывна и дифференцируема на промежутке $[28; 36]$. $y'={2} / {3}⋅{3} / {2}√ {x}-6=√ {x}-6$. $y'=0$ при $x=36$.Так как $y'<0$ на промежутке $[28; 36]$, то функция $y={2} / {3} x√ {x}-6x+2$ является убывающей, следовательно, наименьшее значение принимает в правом конце отрезка $[28; 36]$. $y(36)={2} / {3}⋅ 36⋅√ {36}-6⋅36+2=144-216+2=-70$.

$y=-y={x^2+4} / {x}$

Воспользуемся правилом дифференцирования частного: $(f/g)'={f'·g-f·g'}/{g^2}$

$y'={2x·x-(x^2+4)·1}/{x^2}={x^2-4}/{x^2}$

$y'=0; {x^2-4}/{x^2}=0$

$x^2-4=0$

$x^2=4$

$x_1=2, x_2=-2, x≠0$



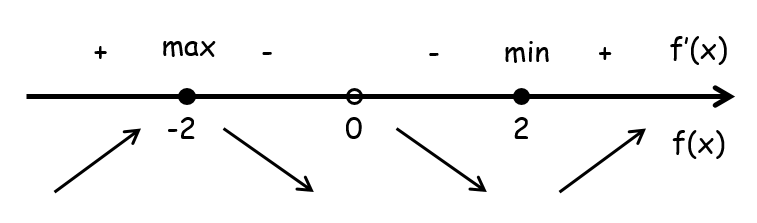
$x_{max}=-2$

$y'=(8x-48)e^{x-48}+(4x^2-48x+48)e^{x-48}=(4x^2-40x)e^{x-48} =4x(x-10)e^{x-48}$. $y'=0$ при $x=0$, $x=10$.

Область определения функции $(-6; +∞)$. $y'={1} / {x+6}-4={-4x-23} / {x+6}$. $y'=0$ при $-4x-23=0$, $x=-5{,}75$. $-5{,}75∈(-6; +∞)$. При переходе через точку $x=-5{,}75$ производная меняет знак с плюса на минус, значит, $x=-5{,}75$ — точка максимума (см. рис. ).

$√ {20-8x-x^2}=√ {36-(x+4)^2}$. Подкоренное выражение неотрицательно при любом допустимом значении $x∈$ и принимает наибольшее значение, равное $36$, при $x=-4$. Наибольшее значение арифметический корень принимает при наибольшем значении подкоренного выражения, значит, наибольшее значение функции $y=√ {20-8x-x^2}$ равно $√ {36}=6$.

Дискриминант квадратного трёхчлена, расположенного под знаком квадратного корня, меньше нуля ($D = 4 - 488$), значит трёхчлен корней не имеет. Ветви параболы, являющейся графиком этого трёхчлена направлены вверх, абсцисса вершины равна $-1$, а ордината $121$. Поэтому $x^2+2x+122 > 0$ при любых x и исходная функция определена при любом значении x из промежутка [-50; 150].

При $-50 ≤ x ≤ -1$ функция $y = x^2 + 2x + 122$ убывает, а значит убывает и функция $y = √{x^2 + 2x + 122}$.

При $-1 ≤ x ≤ 150$ функция $y = x^2 + 2x + 122$ возрастает, а значит возрастает и функция $y = √{x^2 + 2x + 122}$.

Из сказанного следует, что в точке $x = -1$ функция $y = √{x^2 + 2x + 122}$ принимает наименьшее значение на указанном отрезке.

$y(-1) = √{121} = 11$.

Преобразуем подкоренное выражение: $240-8x-x^2 = -(x^2+8x-240) = -((x+4)^2-16-240) = 256-(x+4)^2$. Поэтому $y = √{256 - (x + 4)^2}$.

Так как $(x + 4)^2 ≥ 0$, то $y$ принимает наибольшее значение, если $(x + 4)^2 = 0$, то есть при $x = -4$. Точка $x = -4$ принадлежит заданному промежутку [-18; 10]. Это наибольшее значение равно $√{256} = 16$.

Найдём без применения производной, какие значения принимает функция на отрезке $[12.6; 51]$ и выберем из них наибольшее.

1. Пусть $x$ – произвольное число из отрезка $[12.6; 51]$. Тогда $12.6 ≤ x ≤ 51$. Отсюда по свойствам неравенств получаем: $63 ≤ 5x ≤ 255, 64 ≤ 5x + 1 ≤ 256$.

2. Из предыдущего неравенства, по свойству логарифмов с основанием $0.5$, меньшим $1$, получаем $log_{0.5} 64 ≥ log_{0.5}(5x + 1) ≥ log_{0.5}256$. Но, $log_{0.5}64 = log_{{1}/{2}}64 = log_{{1}/{2}}2^6 = log_{{1}/{2}}(({1}/{2})^{-1})^6 = log_{{1}/{2}}({1}/{2})^{-6} = -6$.

Аналогично, $log_{0.5}256 = -8$. Поэтому $-8 ≤ log_{0.5}(5x + 1) ≤ -6, 6 ≤- log_{0.5}(5x + 1) ≤ 8, 12 ≤ -2 log_{0.5}(5x + 1) ≤ 16$.

Теперь, по свойству квадратного корня получаем, $√12 ≤ √{-2log_{0.5}(5x + 1)} ≤ √{16} = 4$.

Но $√{-2 log_{0.5}(5x + 1)} = y$, поэтому $√{12} ≤ y ≤ 4$.

3. Таким образом, функция определена на всём отрезке $[12.6; 51]$ наибольшим значением является $4$ и получается это значение при $x = 51$.

Заметим, что заданная функция определена и дифференцируема при любом значении $x$

1. Находим $y^′ $, пользуясь правилами дифференцирования и формулой производной степенной функции: $y^′=5x^4-30x^2-135$

2. Решаем уравнение $y^′ =0$. Сделаем подстановку $x^2=t$ ($t⩾0$), получим уравнение $5t^2-30t-135=0$ или $t^2-6t-27=0$. $t_1=-3$, $t_2=9$. $t_1=-3$ не удовлетворяет условию $t⩾0$

Уравнение $x^2=9$ имеет два корня $x_1=-3$, $x_2=3$

На промежуток $[-5 ;0]$, указанный в условии, попадает лишь одно число $x=-3$

Получаем единственную стационарную точку

3. Найдём знак производной на двух интервалах $(-5;-3)$ и $(-3;0)$, на которые точка $x=-3$ разбивает интервал $(-5 ;0)$

Для этого найдем значения производной в точке $x=-4$ из первого интервала, и в точке $x=-1$ из второго интервала. $y^′(-4)=5⋅(-4)^4-30⋅(-4)^2-135=1280-480-135>0$, $y^′(-1)=5⋅(-1)^4-30⋅(-1)^2-135=5-30-135<0$

Производная меняет знак с «плюса» на «минус» при переходе через точку $x=-3$

Следовательно, эта точка является точкой максимума и в ней функция достигает наибольшего значения. $y(-3)=(-3)^5-10⋅(-3)^3-135⋅(-3)=-243+270+405=432$.

Заметим, что заданная функция определена и дифференцируема при любом значении $x$.

1. Находим $y′$, пользуясь правилами дифференцирования и формулой производной степенной функции: $y′ = 5x^4 - 15x^2 - 270$.

2. Решаем уравнение $y′ = 0$. Сделаем подстановку $x^2 = t (t ≥ 0)$, получим уравнение $5t^2 - 15t - 270 = 0$ или $t^2 - 3t - 54 = 0$.

$t_1 = -6, t_2 = 9$.

$t_1 = -6$ не удовлетворяет условию $t ≥ 0$. Уравнение $x^2 = 9$ имеет два корня $x_1 = -3, x_2 = 3$. На промежуток (0; 5) попадает лишь одно число $x = 3$. Получаем единственную стационарную точку.

3. Найдем знак производной на двух промежутках (0; 3) и (3; 5), на которые точка $x = 3$ разбивает интервал (0; 5). Для этого найдем значения производной в точке $x = 1$ из первого интервала, и в точке $x = 4$ из другого интервала.

$y′(1) = 5·1^4 - 15·1^2 - 270 = 5 - 15 - 270 < 0$,

$y′(4) = 5·4^4 - 15·4^2 - 270 = 1280- 240 - 270 > 0$.

Производная меняет знак с "минуса" на "плюс" при переходе через точку $x = 3$. Следовательно, эта точка является точкой минимума и в ней функция достигает наименьшего значения.

$y(3) = 3^5 - 5·3^3 - 270·3 = 243-135-810 = -702$.

Областью определения этой функции является интервал $(0;+∞)$, в каждой точке которого она дифференцируема.

Найдём стационарные точки в области определения и выберем ту из них, в которой производная меняет знак с «минуса» на «плюс».

1. Находим $y^′$, пользуясь правилами дифференцирования, производными степенной и логарифмической функций:

$y^′=0,5⋅ {1} / {2√ x}-{1} / {x}={1} / {4√ x}-{1} / {x}= {x-4√ x} / {4x√ x}={√ x(√ x-4)} / {4x√ x}$. $y^′={√ x(√ x-4)} / {4x√ x}$.

2. Решаем уравнение $y^′=0$, $√ x(√ x-4)=0$.

Так как $√ x>0$, то $√ {x}-4=0$, $√ {x}=4$, $x=16$. Получили одну стационарную точку.

3. Так как $x>0$ и $√ x>0$ в области определения, то знак производной совпадает со знаком функции $y_1=√ {x}-4$

Она обращается в ноль в единственной точке $x=16$.

Находим знак этой функции при $x<16$ и $x>16$.

Для этого достаточно найти её значения хотя бы в одной точке каждого из указанных промежутков:

$y_1(1)=√ {1}-4=-3<0$, а $y_1(25)=√ {25}-4=1>0$

Тем самым, производная меняет знак с «минуса» на «плюс» при переходе через точку $x=16$, которая и будет точкой минимума.

Заметим, что заданная функция непрерывна на отрезке $[-π; 0]$ и дифференцируема на интервале $(-π; 0)$. Наименьшее её значение на отрезке $[-π; 0]$ равно наименьшему из всех значений функции в стационарных точках интервала $(-π; 0)$ и концах отрезка $[-π; 0]$.

1. Находим $y′$, пользуясь правилами дифференцирования и формулами производных тригонометрических функций:

$y′ = -4 + 4 sin x = -4(1 - sin x), y′ = -4(1 - sin x)$.

2. Заметим, что $sin x < 0$ на интервале $(-π; 0)$. Поэтому $1 - sin x > 1$ и $-4(1 - sin x) < 0$. Следовательно, на нём $y′ < 0$ и функция $y=-4x - 4 cos x + 5$ убывает.

3. Наименьшее значение функции будет на правом конце промежутка, то есть в точке $x = 0$.

$y(0) = -4 · 0 - 4 cos 0 + 5 = -4 + 5 = 1$.

Областью определения функции является множество $(-∞; 0) ∪ (0;+∞)$, в каждой точке которого функция дифференцируема. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с "плюса" на "минус".

1. Находим $y′$, представив заданную функцию в виде $y = -9x-{9}/{x}$. По правилам дифференцирования и формуле производной степенной функции получаем: $y′ = -9 + {9}/{x^2} = {-9x^2 +9}/{x^2} = {-9(x^2 - 1)}/{x^2}, y′ = {-9(x^2 - 1)}{x^2}$.

2. Решаем уравнение $y′ = 0, x^2 - 1 = 0, x_1 = -1, x_2 = 1$. Получаем две стационарные точки.

3. Так как $x^2 > 0$ в области определения, то знак производной совпадает со знаком квадратного двучлена $-x^2 +1$, корнями которого являются числа $-1$ и $1$. Поэтому $y′ > 0$ при $x < -1, y′ > 0$ при $-1 < x < 0, y′ > 0$ при $0 < x < 1$ и $y′ < 0$ при $x > 1$.

При переходе через точку $x = 1$ производная меняет знак с "плюса" на "минус". Поэтому эта точка и будет точкой максимума.