Задание 11. Графики функций. ЕГЭ 2026 по математике профильного уровня
Средний процент выполнения: 79%
Ответом к заданию 11 по математике (профильной) может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 11:
Выделить из условия величины и зависимости между ними.
Ввести обозначения и записать зависимость между величинами формулой.
Если в задаче дана функция, установить, какие свойства или график функции нужно использовать по условию.
Построить или преобразовать график функции, если это требуется для решения.
Свести требование задачи к уравнению или системе, соответствующей найденной зависимости.
Найти решения, используя свойства функции и/или график (пересечения, промежутки, расположение графиков).
Проверить, что полученные значения удовлетворяют исходной зависимости и условиям задачи.
Сформулировать итоговый результат в терминах исходной задачи (какая величина и чему равна).
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
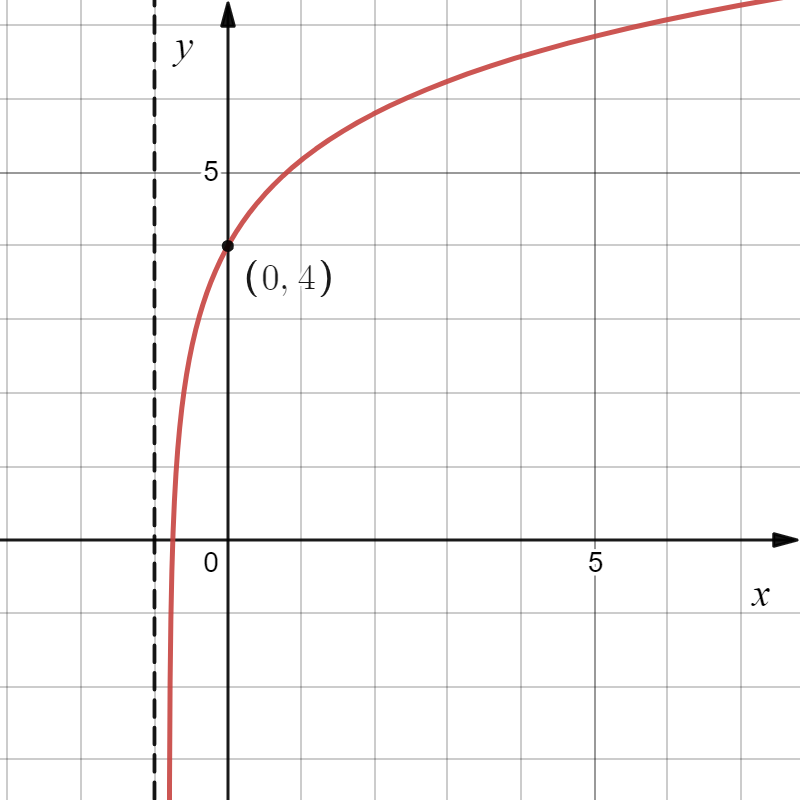
На рисунке изображён график функции вида $ f(x) = log_2(ax + b) + 2 $, где числа $a$, $b$ — целые. Найдите сумму коэффициентов $ a + b $.
Решение
График функции имеет вертикальную асимптоту $ х = -1 $, значит $ -a + b = 0 $
По рисунку видно, что $ f(0) = 4 $, значит:
$ f(0) = log_2(a·0 + b) + 2= 4 $
$ \{\table\-a + b = 0; \ log_2{b} = 2;$
$ b = 4 $
$ a = 4 $
$ a+b = 8$
Задача 2
На рисунке изображён график функции вида $y=kx+b$. Найдите $y(-18)$.
Решение
Посмотри на формулу функции $y = kx + b$. Здесь $k$ — это тангенс угла наклона прямой, а $b$ — это ордината точки пересечения с осью $y$. 📈
1. Определи, в какой точке прямая пересекает ось $y$, чтобы найти $b$.
2. Найди $k$, вычислив тангенс угла наклона прямой. Пользуйся выделенными точками, лежащими в узлах клеток 🌟
3. Как найдешь $k$ и $b$, подставляй $x = -18$ в уравнение функции, чтобы найти $y(-18)$.
Получили $y=0.6x-1.6$
Получили $y(-18)=0.6*(-18)-1.6=-12.4$
Задача 3
На рисунке изображён график функции вида $y=-{1} / {x+a}+c$, где $a$, $c$ — целые числа. Найдите $a$.
Решение
Задача 4
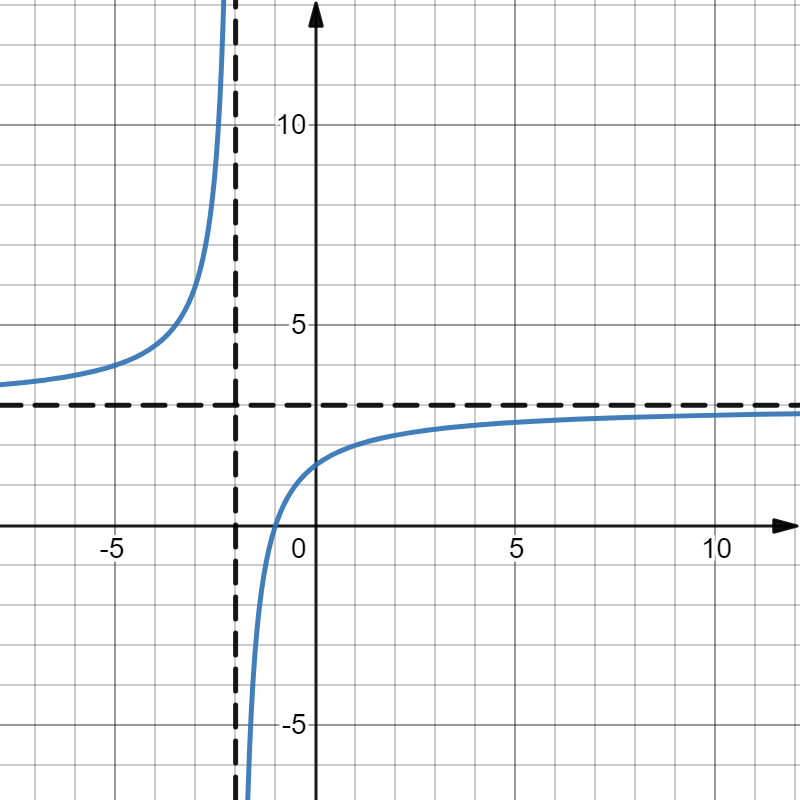
На рисунке изображён график функции вида $ f(x) = {x - 1} / {x + a} + d $. Найдите сумму коэффициентов $ a + b + c $, если функцию записать в виде $ f(x) = b/{x+a} + c $, где числа $a$, $b$,$c$ и $d$ — целые.
Решение
График функции имеет вертикальную асимптоту $ x = -2 $, значит $ a = 2 $
Преобразуем функцию:
$ f(x) = {x - 1} / {x + 2} + d = 1 - {3}/{x+2} + d $
График функции имеет горизонтальную асимптоту $ y = 3 $, значит $ 1 + d = 3 $
$ d = 2 $
$ f(x) = {-3}/ {x + 2} + 3 $
$ b = -3; a = 2; c = 3 $
Задача 5
На рисунке изображён график функции вида $y=ax^2+bx+c$, где числа $a$, $b$ и $c$ — целые. Найдите $b$.
Решение
На рисунке изображён график функции $y=ax^2+bx+c$, где $a<0$,
так как ветви параболы направлены вниз. Если по горизонтальной оси отступить от вершины на $1$ вправо или влево, то можно заметить, что значение функции при этом уменьшается на $3$. Поэтому заданный график получается из графика параболы $y=-3x^2$, смещением на $4$ единицы вправо и на $2$ вверх. Таким образом, изображён график функции $y=-3(x-4)^2+2=-3x^2+24x-46$. Отсюда $b=24$.
Задача 6
На рисунке изображён график функции вида $y=ax^2+bx+c$, где числа $a$, $b$ и $c$ — целые. Найдите $y(-18)$.
Решение
По рисунку в условии задачи заметим, что график получается из графика параболы $y=-x^2$, смещённой на $3$ единицы влево и на $3$ вверх. Таким образом, изображён график функции $y=3-(x+3)^2$. Отсюда $y(-18)=3-(15)^2=-222$.
Задача 7
На рисунке (см. с. ) изображён график функции вида $y=ax^2+bx+c$, где числа $a$, $b$ и $c$ — целые. Найдите $y(-17)$.
Решение
Заметим, что у параболы можно определить координаты вершины, значит мы можем воспользоваться уравнением $y=a(x+m)^2+n$, где $(-m,n)$ - координаты вершины параболы.
По графику определяем координаты вершины: $(-3;5)$, значит $m=3; n=5$.
Получаем уравнение: $y=a(x+3)^2+5$.
Возьмем точку $(-1;1)$ чтобы определить коэффициент $a$. $1=a(-1+3)^2+5 ⇒ a=-1$
Получаем: $y=-(x+3)^2+5$
Найдем $y(-17)$: $y(-17)=-(-17+3)^2+5=-196+5=-191$
Задача 8
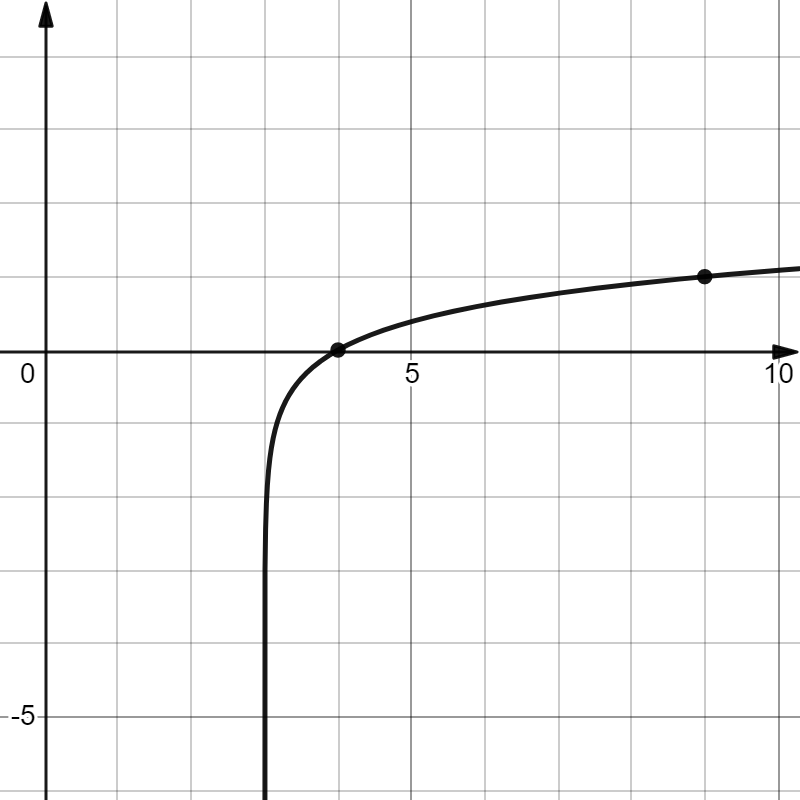
На рисунке изображен график функции ${f(x) = log_{a}(x + b)}$. Найдите $f(219)$
Решение
По рисунку определяем, что ${f(x) = log_6(x -3)}$
Тогда, ${f(219) = log_6(219 -3)=3}$
Задача 9
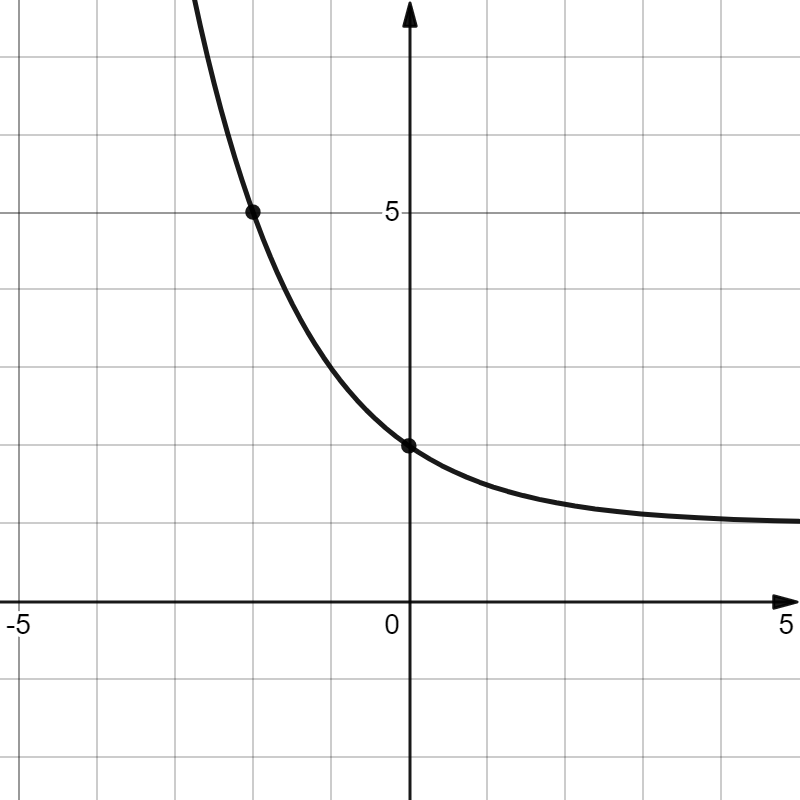
На рисунке изображен график функции $f(x)={{a^x}+{b}}$. Найдите $x$, при котором $f(x)=5$
Решение
По рисунку определяем, что $f(x)={{(1/2)^x}+{1}}$.
Тогда ${(1/2)^x}+{1}={5} ⇒ x=-2$.
Задача 10
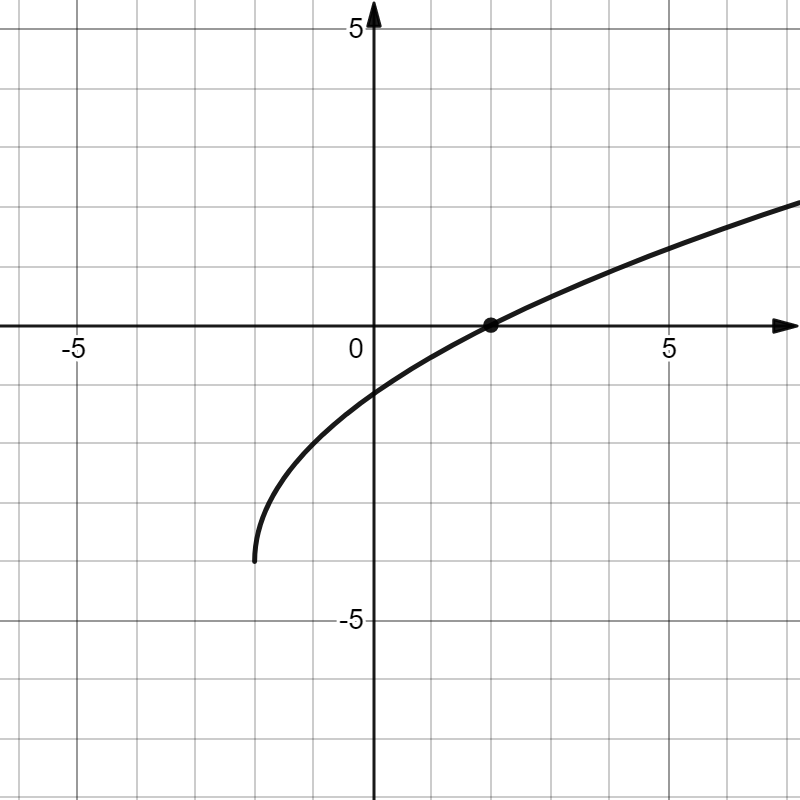
На рисунке изображен график функции $f(x)={{k}{√(x+a)}+{b}}$. Найдите $f(14)$
Решение
Функция задана уравнением: $f(x)={{k}{√(x+a)}+{b}}$, где $(-a,b)$ - координаты начала графика.
По графику определяем координаты начала: $(-2;-4)$, значит $a=2; b=-4$.
Получаем уравнение: $f(x)={{k}{√(x+2)}-{4}}$.
Возьмем точку $(2;0)$ чтобы определить коэффициент $k$. $0={{k}{√(2+2)}-{4}}$
Получаем: $f(x)={{2}{√(x+2)}-{4}}$
Найдем $f(14)$: $f(14)={{2}{√(14+2)}-{4}=4}$
Задача 11
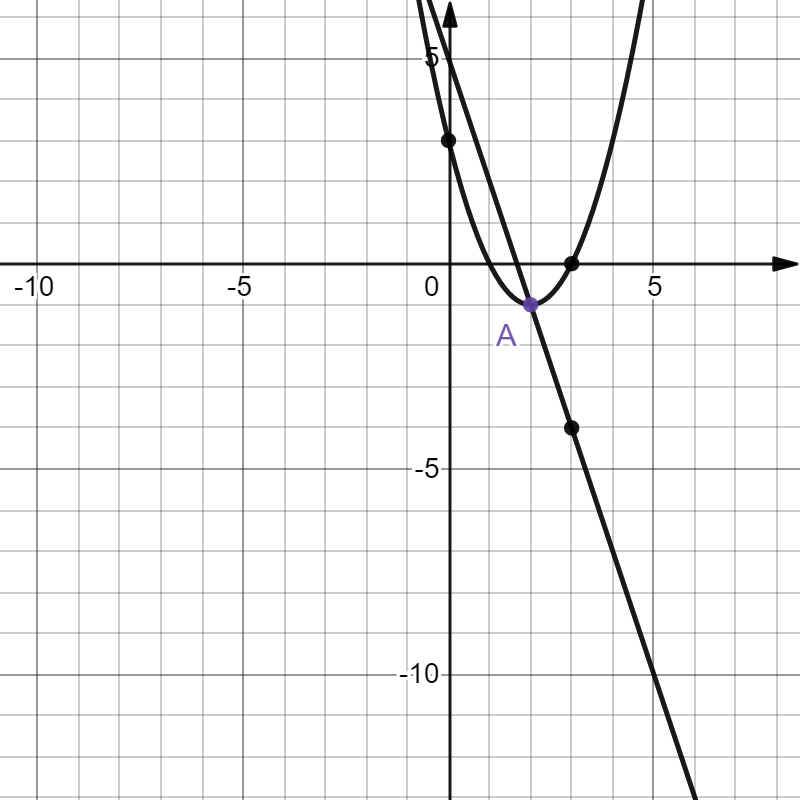
На рисунке изображены графики функции $f(x)={{ax^2}+{bx}+{c}}$ и $g(x)={{kx}+{d}}$, которые пересекаются в точках $A$ и $B$. Найдите абсциссу точки $B$
Решение
По рисунку определяем, что $f(x)={{x^2}-{4x}+{3}}$ и $g(x)={{-3x}+{5}}$
Чтобы найти абсциссу точки пересечения, приравниваем правые части функций:
${{x^2}-{4x}+{3}}={{-3x}+{5}} ⇒ {{x^2}-{x}-{2}=0} ⇒ x_1 = 2; x_2 = -1$
$x_1 = 2$ - абсцисса точки $A$, $x_2 = -1$ - абсцисса точки $B$
Задача 12
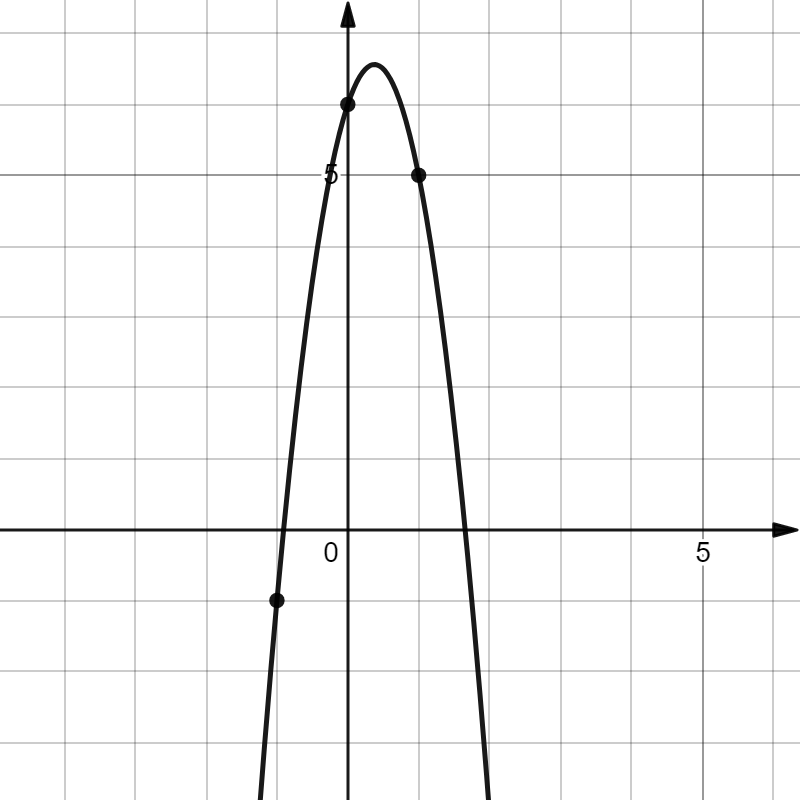
На рисунке изображен график функции $f(x)={{ax^2}+{bx}+{c}}$, где $a, b$, и $c$ - целые числа. Найдите $f(2,5)$
Решение
По рисунку определяем, что $f(x)={{-4x^2}+{3x}+{6}}$
Тогда, $f(2,5)={{-4×(2,5)^2}+{3×2,5}+{6}=-11,5}$
Задача 13
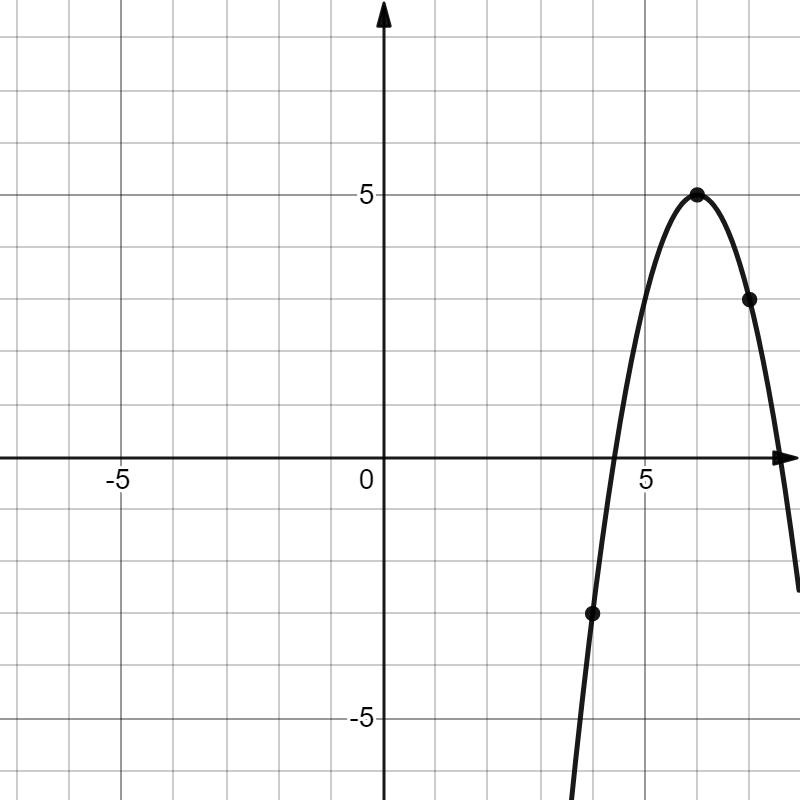
На рисунке изображен график функции $f(x)={{ax^2}+{bx}+{c}}$. Найдите $f(13)$
Решение
По рисунку определяем, что $f(x)={{-2(x-6)^2}+{5}}$
Тогда, $f(13)={{-2(13-6)^2}+{5}=-93}$
Задача 14
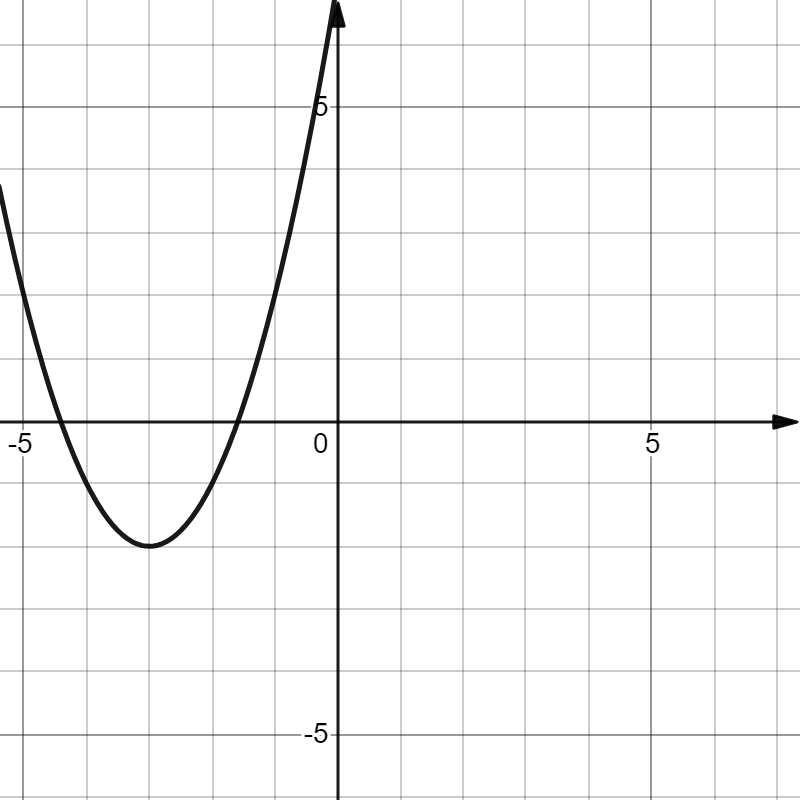
На рисунке изображен график функции $f(x)={{ax^2}+{bx}+{c}}$, где $a, b$, и $c$ - целые числа. Найдите $f(-15)$
Решение
Заметим, что у параболы можно определить координаты вершины, значит мы можем воспользоваться уравнением $y=a(x+m)^2+n$, где $(-m,n)$ - координаты вершины параболы.
По графику определяем координаты вершины: $(-3;-2)$, значит $m=3; n=-2$.
Получаем уравнение: $y=a(x+3)^2-2$.
Возьмем точку $(-1;2)$ чтобы определить коэффициент $a$. $2=a(-1+3)^2-2 ⇒ a=1$
Получаем: $y=(x+3)^2-2$
Найдем $f(-15)={{(-15+3)^2}-{2}=142}$
Задача 15
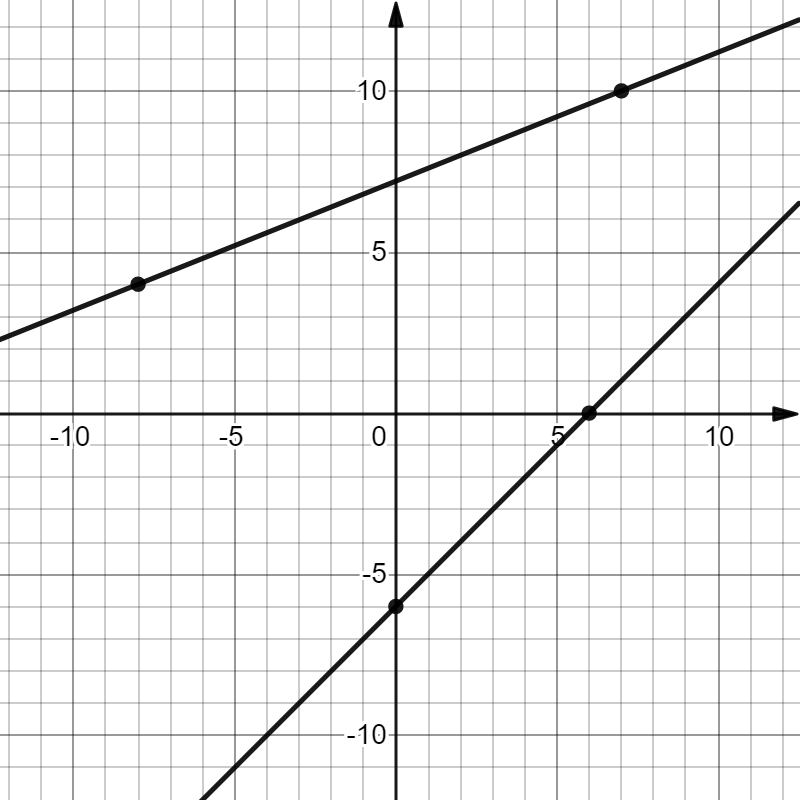
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков
Решение
По рисунку определяем, что $f(x)={{x}-{6}}$ и $g(x)={{0,4x}+{7,2}}$.
Чтобы найти абсциссу точки пересечения графиков, приравняем правые части функций: ${{x}-{6}}={{0,4x}+{7,2}} ⇒ {x=22}$ - абсцисса точки пересечения
Задача 16
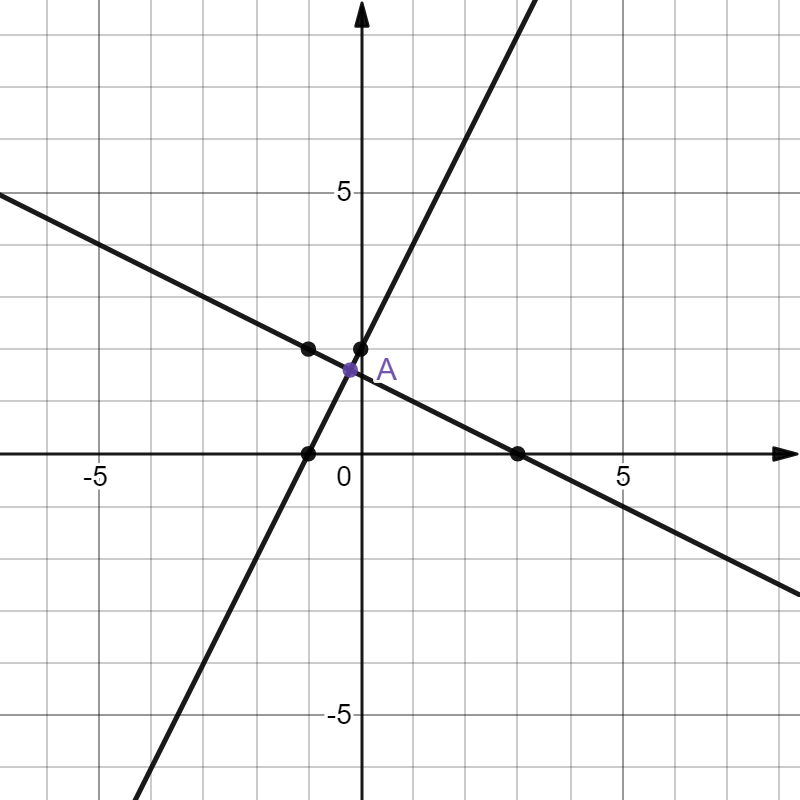
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков
Решение
По рисунку определяем, что $f(x)={{2x}+{2}}$ и $g(x)={{-0,5x}+{1,5}}$.
Чтобы найти абсциссу точки пересечения графиков, приравняем правые части функций: ${{2x}+{2}}={{-0,5x}+{1,5}} ⇒ {x=-0,2}$ - абсцисса точки пересечения
Задача 17
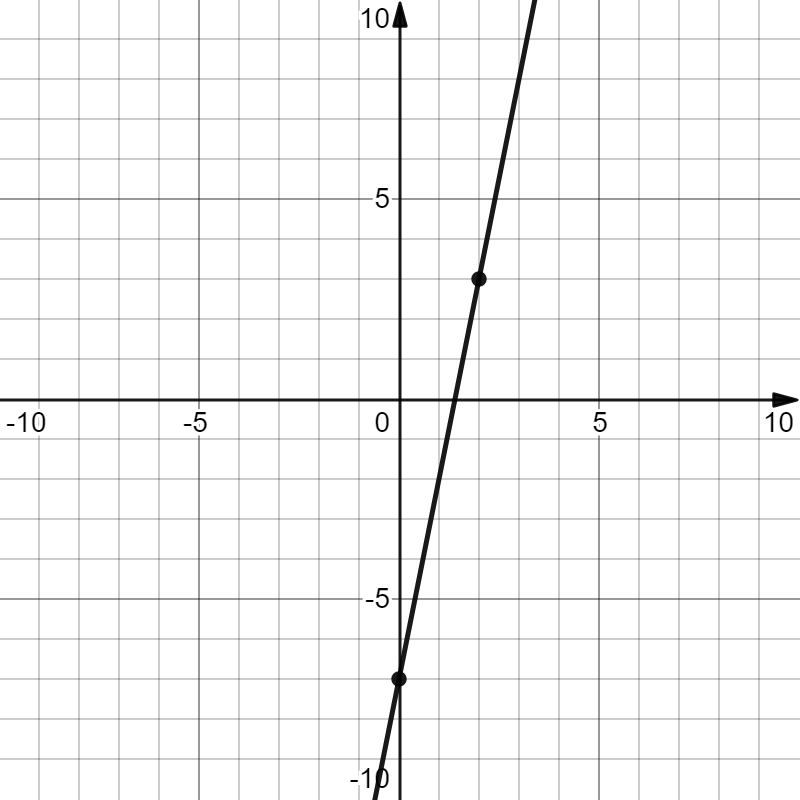
На рисунке изображен график функции вида $f(x)={{kx}+{b}}$. Найдите значение $f(-3)$.
Решение
По рисунку определяем, что $f(x)={{5x}-{7}}$. Тогда $f(-3)={{5×(-3)}-{7}=-22}$.
Задача 18
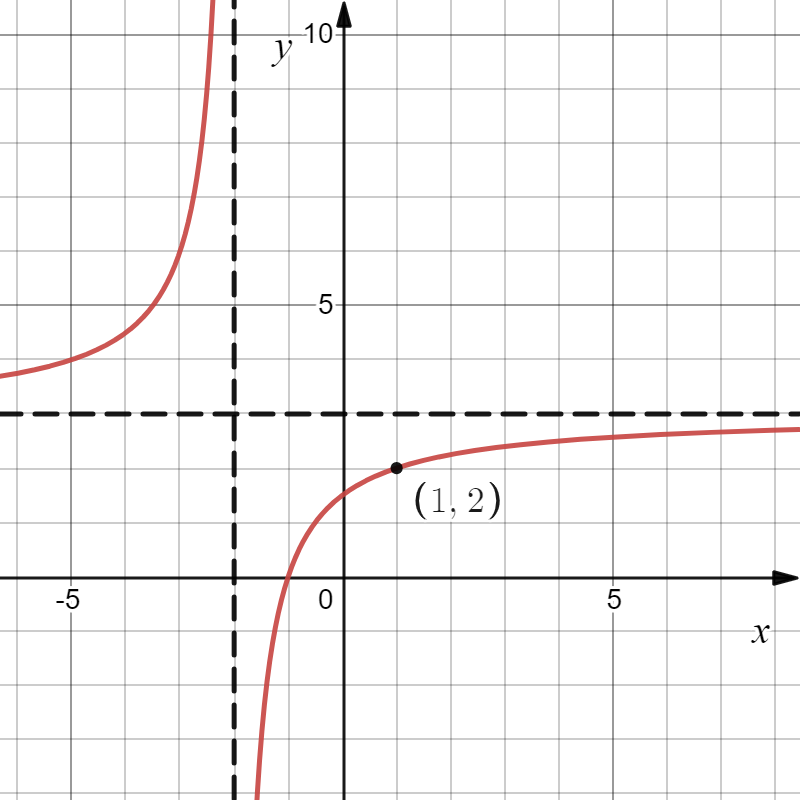
На рисунке изображён график функции вида $ f(x) = {a}/{x+b} + c $, где числа $a$, $b$ и $c$ — целые. Найдите решение уравнения $ f(x) = 18 $.
Решение
График функции имеет горизонтальную асимптоту $ y = 3 $, значит $ с = 3 $
График функции имеет вертикальную асимптоту $ х = -2 $, значит $ b = 2 $
По рисунку видно, что $ f(1) = 2 $, значит:
$ f(1) = {a}/{1 + 2} + 3 = 2 $
$ a = -3 $
$ f(x) = 18 ⇔ {-3}/{x+2} + 3 = 18 $
$ {-3}/{x+2} = 15 ⇔ 15x = - 33 $
Задача 19
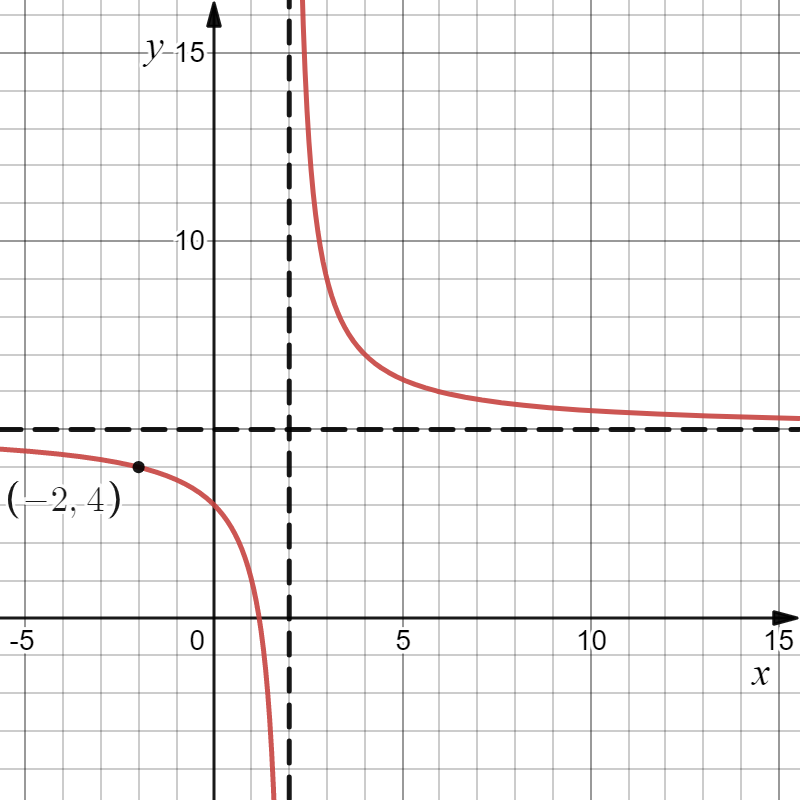
На рисунке изображён график функции вида $ f(x) = {a}/{x+b} + c $, где числа $a$, $b$ и $c$ — целые. Найдите $x$, при котором $ f(x) = 21 $.
Решение
График функции имеет горизонтальную асимптоту $ y = 5 $, значит $ с = 5 $
График функции имеет вертикальную асимптоту $ х = 2 $, значит $ b = -2 $
По рисунку видно, что $ f(-2) = 4 $, значит:
$ f(-2) = {a}/{-2 -2} + 5 = 4 $, значит $ a = 4 $.
Тогда $ f(x) = {4}/{x-2} + 5 $, значит:
$ f(x) = 21 $.
${4}/{x-2} + 5 = 21 $.
Задача 20
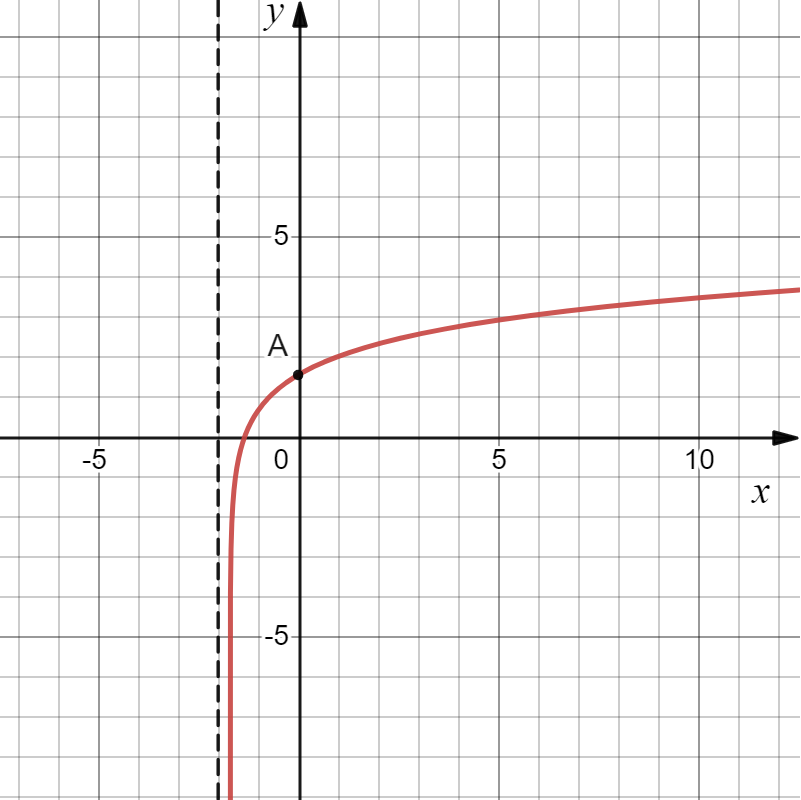
На рисунке изображён график функции вида $ f(x) = ln(a + x) + b $, где числа $a$, $b$ — целые. Найдите сумму коэффициентов $ a + b $, если $A( 0 ; ln2e ) $.
Решение
График функции имеет вертикальную асимптоту $ х = -2 $, значит $ a = 2 $
По рисунку видно, что $ f(0) = ln(2e) $, значит:
$ f(0) = ln(2 + 0) + b = ln(2e) $
$ ln(2) + b = ln(2) + ln (e) $
$ ln(2) + b = ln(2) + 1 $
$ b = 1 $
Рекомендуемые курсы подготовки

- Узнаешь, как выглядят графики функций.
- Разберешься, как по данному графику определить, какая функция задана.
- Научишься решать все прототипы 11 задания профильной математики.
- Получишь море полезных материалов.
на бесплатном курсе Турбо ЕГЭ

