Задание 3. Стереометрия. ЕГЭ 2026 по математике профильного уровня
Средний процент выполнения: 68%
Ответом к заданию 3 по математике (профильной) может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 3:
Определи, какие геометрические объекты фигурируют в условии (точка, прямая, плоскость, фигура) и какая величина требуется (длина, угол, площадь, объём, площадь поверхности, расстояние).
Выдели в условии связи между объектами: угол между прямыми/плоскостями, угол между прямой и плоскостью, расстояние от точки до плоскости, расстояние между прямыми/плоскостями, свойства подобия или равенства фигур.
Сопоставь ситуацию с подходящими геометрическими отношениями и с теми фактами и теоремами планиметрии, которые применимы к данному случаю.
Если в условии требуется переход к вычислениям, зафиксируй необходимые элементы для расчёта (отрезки, углы, элементы поверхности/фигуры).
Вычисли искомую геометрическую величину (длина, угол, площадь, объём, площадь поверхности), используя изученные формулы и методы, соответствующие выбранным отношениям.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
В сосуде, имеющем форму конуса, уровень жидкости достигает ${1} / {5}$ высоты (см. рис. ). Объём сосуда $1500$ мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
Решение
Обозначим объём большего конуса $V_1$, а объём меньшего конуса (жидкости) $V_2$. Меньший конус подобен большему конусу с коэффициентом подобия ${1} / {5}$. Отношение объёмов подобных тел равно кубу коэффициента подобия ${V_2} / {V_1}=k^3$, то есть ${V_2} / {1500}=({1} / {5})^3$, $V_2={1} / {125}⋅1500=12$ (мл).
Задача 2
Объём второго цилиндра равен $20$ м$^3$. У первого цилиндра высота в $1{,}6$ раза больше, а радиус основания в $2$ раза меньше, чем у второго. Найдите объём первого цилиндра (см. рис. ).
Решение
Формула для объёма цилиндра:
$V = \π r^2 h$,
где $r$ — радиус основания, $h$ — высота цилиндра.Обозначим радиус основания второго цилиндра за $r_2$, а его высоту — за $h_2$. Тогда объём второго цилиндра:
$V_2 = \π r_2^2 h_2 = 20$ м$^3$.
У первого цилиндра радиус основания $r_1$ в $2$ раза меньше, чем у второго цилиндра, то есть:
$r_1 = {r_2} / 2$.
Также высота первого цилиндра $h_1$ в $1,6$ раза больше, чем у второго цилиндра:
$h_1 = 1.6 h_2$.
Теперь найдём объём первого цилиндра:
$V_1 = \π r_1^2 h_1 = \π ({r_2} / 2)^2 (1.6 h_2)= 0.4 \π r_2^2 h_2= 0.4 * 20 = 8$.
Ответ: $8$ .
Задача 3
Найдите объём многогранника, вершинами которого являются точки $A$, $B$, $D$, $E$, $A_1$, $B_1$, $D_1$, $E_1$ правильной шестиугольной призмы $ABCDEFA_1B_1C_1D_1E_1F_1$ (см. рис. , с. ). Площадь основания призмы равна $15$, а боковое ребро равно $4$.
Решение
Объём призмы $ABDEA_1B_1D_1E_1$ найдём по формуле
$V_{п.}=S_{ABDE}⋅ AA_1$, где $S_{ABDE}$ — площадь основания, $AA_1$ — высота призмы (см. рис. $$). По условию призма $ABCDEFA_1B_1C_1D_1E_1F_1$ — правильная, следовательно, $ABCDEF$ — правильный шестиугольник с центром в точке $O$. По свойству правильного шестиугольника треугольник $BOC$ равносторонний и $S_{BOC}={S_{ABCDEF}} / {6}={15} / {6}={5} / {2}$. $S_{BCD}={BC⋅ CD} / {2}⋅\sin120°$, $S_{BOC}={OB⋅ OC} / {2}⋅\sin60°$. Так как $BC=CD=OB=OC$ и $\sin120°=\sin60°$, то $S_{BCD}=S_{BOC}={5} / {2}$, $▵ AFE=▵ BCD$ по двум сторонам и углу между ними. Тогда $S_{AFE}=S_{BOC}={5} / {2}$, $S_{AFE}+S_{BCD}=2S_{BOC}={5} / {2}⋅2=5$. $S_{ABDE}=S_{ABCDEF}-2S_{BOC}=15-5=10$,
$V_{ABDEA_1B_1D_1E_1}=10⋅4=40$.
Задача 4
Объём второго шара в $27$ раз меньше объёма первого. Во сколько раз площадь поверхности первого шара больше площади поверхности второго шара?
Решение
Обозначим $r_1$ — радиус первого шара, а $r_2$ — радиус второго шара. Составим отношение объёмов ${V_1} / {V_2}={{4} / {3}π r_1^3} / {{4} / {3}π r_2^3}={r_1^3} / {r_2^3}=27$, ${r_1} / {r_2}=√^3{27}=3$. Радиус первого шара больше радиуса второго шара в $3$ раза, тогда $r_1=3r_2$. Найдём искомое отношение ${S_1} / {S_2}={4π r_1^2} / {4π r_2^2}={(3r_2)^2} / {r^2}=9$.
Задача 5
Найдите объём многогранника, вершинами которого являются точки $A$, $B$, $C$, $B_1$ прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=3$, $AD=7$, $AA_1=5$ (см. рис. ).
Решение
Многогранник $B_1ABC$ — пирамида. Объём пирамиды
$V_{п.}={1} / {3}S_{ABC}⋅ BB_1$, где $S_{ABC}$ — площадь основания, $BB_1$ — высота
(см. рис. ). $S_{ABC}={1} / {2}S_{ABCD}={AB⋅ AD} / {2}={3⋅7} / {2}=10{,}5$, $BB_1=AA_1=5$. $V_{B_1ABC}={1} / {3}⋅10{,}5⋅5=17{,}5$.
Задача 6
Объём первого цилиндра равен $16$ м$^3$. У второго цилиндра высота в $3$ раза больше, а радиус основания в $2$ раза меньше, чем у первого. Найдите объём второго цилиндра (см. рис. ). Ответ дайте в кубических метрах.
Решение
Пусть $r$ и $h$ — радиус основания и высота первого цилиндра, а $V_1=π r^2 h$ — его объём. Тогда объём второго цилиндра $V_2=π⋅({r} / {2})^2⋅ 3h$. ${V_1} / {V_2}={π r^2h} / {π⋅({r} / {2})^2⋅ 3h}={4} / {3}$. Отсюда $V_2={3V_1} / {4}={3⋅16} / {4}=12$.
Задача 7
Объём части цилиндра, изображённой на рисунке , равен $4{,}5π$. Найдите высоту цилиндра, если радиус основания цилиндра равен $1{,}5$, а угол $α=120^°$.
Решение
Оставшийся угол цилиндра равен $360^° - 120^° = 240^°$. Объём оставшейся части составляет $240^°/360^°$ от полного объёма цилиндра. Полный объём цилиндра выражается как:
$V = πr^2h$, {где $r$ — радиус основания, $h$ — высота цилиндра.}
Используем пропорцию объёма:
$(240^°/360^°) * πr^2h = 4{,}5π$.
Подставляем $r = 1{,}5$:
$(2/3) * π * (1{,}5)^2 * h = 4{,}5π$.
Упрощаем:
$(2/3) * π * 2{,}25 * h = 4{,}5π$.
$1{,}5h = 4{,}5$.
$h = {4{,}5} / {1{,}5} = 3$.
{Ответ:} $3$.
Задача 8
В сосуде, имеющем форму конуса, уровень жидкости достигает ${1} / {2}$ высоты (см. рис. ). Объём жидкости $60$ мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение
Обозначим объём большего конуса $V_1$, а объём меньшего конуса $V_2$. Меньший конус подобен большему конусу с коэффициентом подобия ${1} / {2}$. Отношение объёмов подобных тел равно кубу коэффициента подобия ${V_2} / {V_1}=k^3$, то есть ${60} / {V_1}=({1} / {2})^3$, $V_1=60⋅8=480$ (мл). Жидкости нужно долить $480-60=420$ (мл).
Задача 9
Стороны основания правильной четырёхугольной пирамиды равны $16$, боковые рёбра равны $17$ (см. рис. $$). Найдите площадь поверхности этой пирамиды.
Решение
Площадь поверхности пирамиды $S=S_{бок.}+S_{осн.}$, где $S_{бок.}$ — площадь боковой поверхности, $S_{осн.}$ — площадь основания пирамиды. По условию пирамида $SABCD$ правильная, значит, боковые рёбра равны, $ABCD$ — квадрат. $S_{бок.}={1} / {2}Ph_a$, где $P$ — периметр основания, $h_a$ — высота боковой грани (апофема) (см. рис. $$). Треугольник $ASB$ равнобедренный, $SH$ высота, тогда $SH$ — медиана и $BH=AH=8$. По теореме Пифагора в $▵ SHB$ $SB^2=SH^2+BH^2$, $SH=√ {SB^2-BH^2}=√ {17^2-8^2}=√ {225}=15$. $S_{бок.}={1} / {2}⋅4⋅16⋅15=480$, $S_{ABCD}=16^2=256$, $S=480+256=736$.
Задача 10
Площадь поверхности куба равна $72$ (см. рис., с. ). Найдите его диагональ.
Решение
Площадь поверхности куба $S_{пов.}=6a^2$, где $a$ — сторона куба, $6a^2=72$, $a=√ {{72} / {6}}=√ {12}$. Диагональ куба $d=a√ 3$, $d=√ {12}⋅√ 3=√ {36}=6$.
Задача 11
Найдите объём призмы (см. рис. ), в основании которой лежит правильный шестиугольник со стороной $4$, а боковые рёбра равны $4√ {3}$ и наклонены к плоскости основания под углом $30^°$.
Решение
Объём призмы $V=Sh$, где $S$ — площадь шестиугольника, $h$ — высота призмы, равная длине перпендикуляра, опущенного из какой-либо вершины верхнего основания на плоскость нижнего основания призмы (см. рис. $$). Пусть $a$ — сторона основания призмы, $l$ — боковое ребро. По условию шестиугольник правильный, значит,
$S={6⋅ a^2√ 3} / {4}={3a^2√ 3} / {2}$, $h={1} / {2}l$ как катет прямоугольного треугольника, лежащий против угла $30°$. Тогда объём призмы $V={3a^2√ 3} / {2}⋅{l} / {2}$, $V={3⋅4^2⋅√ 3} / {2}⋅{4√ 3} / {2}=144$.
Задача 12
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен $3$ (см. рис. ). Найдите объём куба.
Решение
Так как высота куба равна высоте призмы, то их объёмы пропорциональны площадям их оснований. По рисунку $$ определяем, что площадь основания отсечённой призмы $S_{M_1N_1C_1}$ в $8$ раз меньше площади основания куба $S_{A_1B_1C_1D_1}$. $V_{куба}=8V_{MNCM_1N_1C_1}, V_{куба}=8⋅3=24$.
Задача 13
Дано два шара (см. рис. ). Радиус первого шара в $20$ раз больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго шара?
Решение
Дано два шара. Радиус первого шара в $20$ раз больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго шара?
Площадь поверхности шара определяется формулой $S = 4πR^2$, где $R$ — радиус шара.
Пусть радиус второго шара равен $R$, тогда радиус первого шара равен $20R$.
Площадь поверхности второго шара:
$S_2 = 4πR^2$.
Площадь поверхности первого шара:
$S_1 = 4π(20R)^2 = 4π*400R^2 = 1600πR^2$.
Отношение площадей:
$S_1 / S_2 = {1600πR^2 }/ {4πR^2 }= 1600 / 4 = 400.$
Ответ: $400$.
Задача 14
В сосуд, имеющий форму правильной треугольной призмы, налили $1200$ см$^3$ жидкости (см. рис. ) и полностью погрузили в неё деталь. При этом уровень жидкости в сосуде поднялся с отметки $24$ см до отметки $32$ см. Найдите объём детали. Ответ дайте в кубических сантиметрах.
Решение
Зная объём и уровень налитой жидкости, найдём площадь основания сосуда $V=S_{осн.}⋅ h$, $S_{осн.}={V} / {h}$, $S_{осн.}={1200} / {24}=50$ см$^2$. Уровень жидкости поднялся на $32-24=8$ (см). Объём детали равен объёму вытесненной ею жидкости $V_{дет.}=50⋅8=400$ см$^3$.
Задача 15
В основании прямой призмы лежит ромб с диагоналями, равными $20$ и $48$ (см. рис.). Площадь её поверхности равна $1272$. Найдите боковое ребро этой призмы.
Решение
Так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам, то сторону ромба найдём из прямоугольного треугольника $AOD$ по теореме Пифагора.
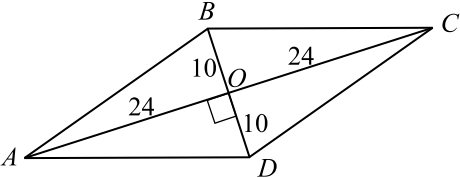
$AD = √{AO^2 + OD^2} = √{24^2 + 10^2} = 26$.
Площадь ромба $S_{осн} = {1}/{2}d_1 · d_2$, где $d_1$ и $d_2$ — диагонали ромба. $S_{осн} = {1}/{2} · 48 · 20 = 480$. Пусть боковое ребро призмы равно $x$. Площадь поверхности призмы равна $S = S_{бок} + 2S_{осн} = 1272$, откуда $S_{бок} = 1272 - 960 = 312$. Так как $S_{бок} = 4 · 26 · x$, то $104x = 312$, откуда $x = 3$.
Задача 16
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен $7$.
Решение
$V_{цилиндра}=S_{осн}⋅ H$, $V_{конуса}={1} / {3} S_{осн}⋅ H$. По условию конус
и цилиндр имеют общее основание и общую высоту, значит,
$V_{цилиндра}=3V_{конуса}=21$.
Задача 17
Площадь основания конуса равна $27$. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной $2$ и $4$, считая от вершины (см. рис.). Найдите площадь сечения конуса этой плоскостью.
Решение
Пусть $CA = R$ - радиус основания конуса, сечение конуса плоскостью, параллельной плоскости основания конуса - круг, радиус которого $OD = r$.
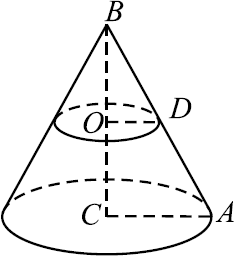
$OD ‖ AC$, следовательно, $△ABC ∼ △DBO$ по первому признаку подобия ($∠ACB = ∠DOB = 90°, ∠ABC$ - общий). По условию $BO = 2, OC = 4$, значит, $BC = 6$, откуда ${BO}/{BC} = {OD}/{AC} = {1}/{3}, {πr^2}/{πR^2} = {1}/{9}$. Значит, площадь сечения конуса плоскостью, параллельной плоскости основания конуса, в $9$ раз меньше плоскости основания конуса, то есть равна $27 : 9 = 3$.
Задача 18
Если каждое ребро куба увеличить на 3, то его площадь поверхности увеличится на 126. Найдите ребро куба.
Решение
$S_1=6а^2$
$ S_2=6(a+3)^2$
$ 6(a+3)^2-6а^2=126$
$ 6(а^2+6а+9)-6а^2=126$
$ 6а^2+36а+54-6а^2=126$
$ 36а=126-54$
$ 36а=72$
$ а=2$.
Задача 19
В правильной четырёхугольной пирамиде высота равна $3$, объём равен $32$ (cм. рис.). Найдите боковое ребро этой пирамиды.
Решение
Объём пирамиды вычисляется по формуле $V = {1}/{3}·S_{осн}·H$, где $H = 3$ - высота пирамиды. Площадь основания равна $S_{осн} = 3{V}/{H} = {3·32}/{3} = 32$, откуда длина стороны квадрата, лежащего в основании пирамиды, равна $√{32} = 4√2$. Диагональ квадрата $AC = 8$.
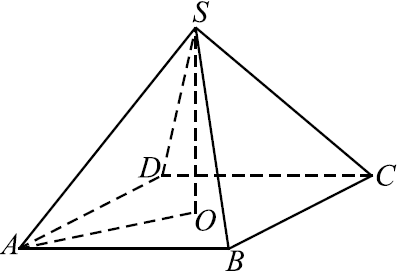
Боковое ребро $SA$ найдём как гипотенузу прямоугольного треугольника $AOS$, где $SO$ - высота пирамиды. $AS = √{SO^2 + OA^2} = √{SO^2 + ({1}/{2}AC)^2} = √{3^2 + 4^2} = 5$.
Задача 20
В правильной четырёхугольной пирамиде высота равна $9$, объём равен $864$ (cм. рис.). Найдите боковое ребро этой пирамиды.
Решение
Объём пирамиды вычисляется по формуле $V = {1}/{3}·S_{осн}·H$, где $H = 9$ - высота пирамиды. Площадь основания равна $S_{осн} = 3{V}/{H} = {3·864}/{9} = 288$, откуда длина стороны квадрата, лежащего в основании пирамиды, равна $√{288} = 12√2$. Диагональ квадрата $AC = 24$.
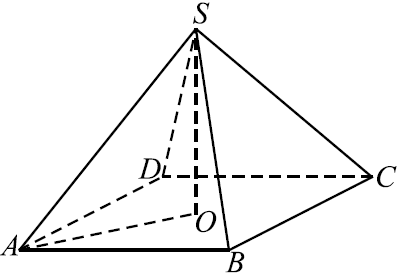
Боковое ребро $SA$ найдём как гипотенузу прямоугольного треугольника $AOS$, где $SO$ - высота пирамиды. $AS = √{SO^2 + OA^2} = √{SO^2 + ({1}/{2}AC)^2} = √{9^2 + 12^2} = 15$.
Рекомендуемые курсы подготовки

- Получишь все формулы, которые нужны для решения ЛЮБОЙ задачи по теории вероятностей в ЕГЭ по профилю
- Научишься решать задачи №4.5 в ЕГЭ по профилю
- Улучшить свой результат на +15 вторичных баллов
на бесплатном курсе Турбо ЕГЭ

