Задание 2. Векторы и операции с ними. ЕГЭ 2026 по математике профильного уровня
Средний процент выполнения: 93%
Ответом к заданию 2 по математике (профильной) может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 2:
Выдели в условии, какие величины заданы: координаты точки/вектора, компоненты вектора, указание на сумму векторов, умножение вектора на число, скалярное произведение, угол между векторами.
Если требуется, определи координаты нужной точки или вектора из данных условия.
Выполни операции над векторами, которые указаны в условии (сумма векторов, умножение на число).
Если требуется, вычисли длину вектора и/или его координаты после выполненных операций.
Если требуется, используй скалярное произведение и полученные координаты/длины, чтобы найти искомую величину, связанную с векторами.
Если в условии требуется угол между векторами, вычисли его на основе данных о векторах и выполненных вычислений.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
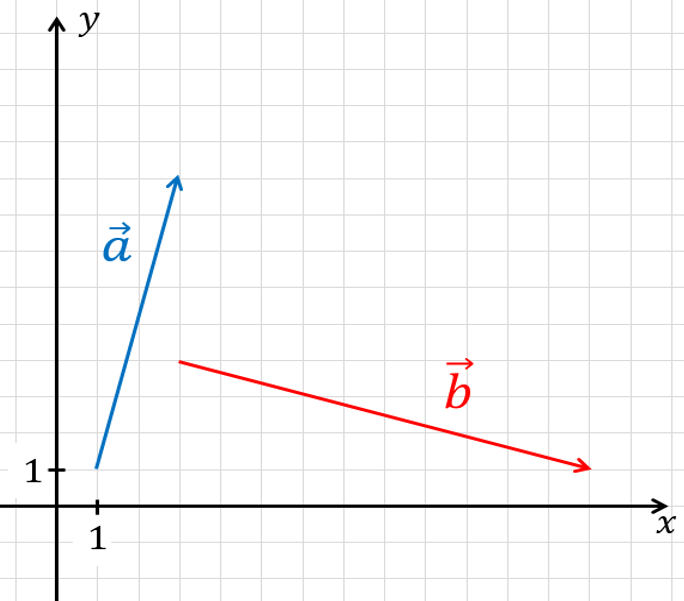
На координатной плоскости изображены векторы ${{a}↖{→}}$ и ${{b}↖{→}}$. Найдите скалярное произведение ${{a}↖{→}}∙$${{b}↖{→}}$
Решение
Определим по рисунку координаты векторов.
${{a}↖{→}}\{2; 8\}$ и ${{b}↖{→}}\{10; -3\}$
Найдем скалярное произведение ${{a}↖{→}}∙$${{b}↖{→}}$:
${{a}↖{→}}∙$${{b}↖{→}}$= ${x_a}∙{x_b}+{y_a}∙{y_b}={2}∙{10}+{8}∙{(-3)}=-4$
Задача 2
Даны векторы ${{a}↖{→}}$$(-3;4)$, ${{b}↖{→}}$$(-1;-7)$ и ${{c}↖{→}}$$(5;-4)$. Найдите координаты вектора ${{a}↖{→}}+$${{b}↖{→}}-$${{c}↖{→}}$. В ответ запишите сумму координат
Решение
Найдем координаты вектора ${{a}↖{→}}+$${{b}↖{→}}-$${{c}↖{→}}$= $({x_a}+{x_b}-{x_c};{y_a}+{y_b}-{y_c})=({-3}+{(-1)}-{5};{4}+{(-7)}-{(-4)})=({-9};{1})$
найдем сумму координат: $-9+1=-8$
Задача 3
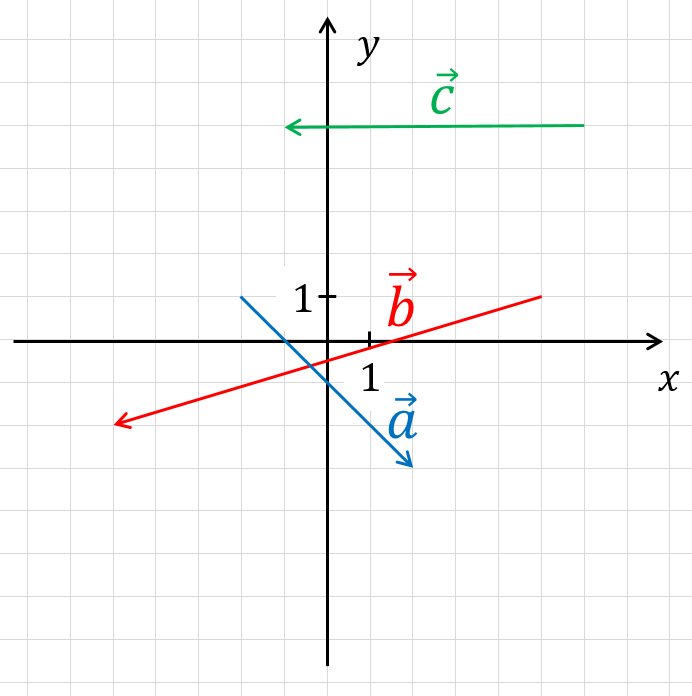
На координатной плоскости изображены векторы ${{a}↖{→}}$, ${{b}↖{→}}$ и ${{c}↖{→}}$. Найдите скалярное произведение ${{a}↖{→}}∙$$({{b}↖{→}}+$${{c}↖{→}})$
Решение
Определим по рисунку координаты векторов.
${{a}↖{→}}\{4; -4\}$, ${{b}↖{→}}\{-10; -3\} и {{c}↖{→}}\{-7; 0\}$
Найдем сумму векторов ${{b}↖{→}}+$${{c}↖{→}}$= $({x_b}+{x_c};{y_b}+{y_c})=({-17};{-3})$
Найдем скалярное произведение ${{a}↖{→}}∙$$({{b}↖{→}}+$${{c}↖{→}})$= ${x_a}∙{x_{b+c}}+{y_a}∙{y_{b+c}}={4}∙{(-17)}+{(-4)}∙{(-3)}=-56$
Задача 4
Даны векторы ${{a}↖{→}}$$(-4;5)$, ${{b}↖{→}}$$(3;-1)$ и ${{c}↖{→}}$$(2;c_0)$. Найдите $c_0$, если (${{a}↖{→}}$+${{b}↖{→}}$)∙${{c}↖{→}}$=0
Решение
Дано: векторы ${{a}↖{→}}$= $(-4; 5)$, ${{b}↖{→}}$ = $(3; -1)$ и ${{c}↖{→}}$ = $(2; c_0)$.
Необходимо найти $c_0$, если ($ {{a}↖{→}}$ + ${{b}↖{→}} $) ⋅ ${{c}↖{→}} $= 0.
1). Сначала найдем вектор суммы ${{a}↖{→}}$ + ${{b}↖{→}}$:
${{a}↖{→}}$ + ${{b}↖{→}}$ = $(-4 + 3; 5 + (-1)) = (-1; 4)$.
2). Теперь вычислим скалярное произведение $({{a}↖{→}} + {{b}↖{→}})⋅{{c}↖{→}}$:
$({{a}↖{→}} + {{b}↖{→}})⋅{{c}↖{→}}= (-1) ⋅ 2 + 4 ⋅c_0 = -2 + 4c_0$.
3). Из условия задачи получаем уравнение: $-2 + 4c_0 = 0$.
Решаем уравнение: $4c_0 = 2$, отсюда $c_0 = 0,5$.
Ответ: $c_0 = 0,5$.
Задача 5
Найдите координаты вектора ${{a}↖{→}}+$${{b}↖{→}}$, если ${{a}↖{→}}$$(-4;6)$, ${{b}↖{→}}$$(2;-7)$. В ответ запишите сумму координат вектора ${{a}↖{→}}+$${{b}↖{→}}$
Решение
Найдем координаты вектора ${{a}↖{→}}$+${{b}↖{→}}$= $({x_a}+{x_b};{y_a}+{y_b})=({-4}+{(2)};{6}+{(-7)})=({-2};{(-1)})$
найдем сумму координат: $-2+(-1)=-3$
Задача 6
Даны векторы ${{a}↖{→}}$$(3;y_a)$, ${{b}↖{→}}$$(x_b;0)$, косинус угла между которыми равен ${3}/{√13}$. Найдите $y_a$. Если таких значений несколько, в ответ запишите большее из них.
Решение
Дано: векторы ${{a}↖{→}}$ = $(3; y_a)$ и ${{b}↖{→}}$ = $(x_b; 0)$, косинус угла между которыми равен $ {3}/{√{13}}$. Необходимо найти $y_a$.
Используем формулу для косинуса угла между векторами:
$\cos∠({{a}↖{→}},{{b}↖{→}})={{{a}↖{→}}⋅ {{b}↖{→}}} / {|{{a}↖{→}}|⋅{|{{b}↖{→}}|}}$.
Скалярное произведение векторов ${{a}↖{→}} = (3, y_a)$ и ${{b}↖{→}} = (x_b, 0)$ равно:
${{a}↖{→}}⋅{{b}↖{→}} = 3⋅ x_b + y_a⋅ 0 = 3 x_b$.
Длины векторов находим по формуле: ${{|c|}↖{→}}$=$√{x^2+y^2}$
$|{{a}↖{→}}| = √{9 + y_a^2}$ и $|{{b}↖{→}}| = |x_b|$.
Подставляем это в формулу для косинуса:
${3}/{√{13}}={3 x_b} / {√{9 + y_a^2}⋅|x_b|}$.
Решаем уравнение. Для случая $x_b > 0$ получаем:
$ {√{9 + y_a^2} = {√{13}$, отсюда $y_a^2 = 4$.
Таким образом, $y_a = ± 2$. Нам нужно выбрать большее значение, то есть $y_a = 2$.
Ответ: $y_a = 2$.
Задача 7
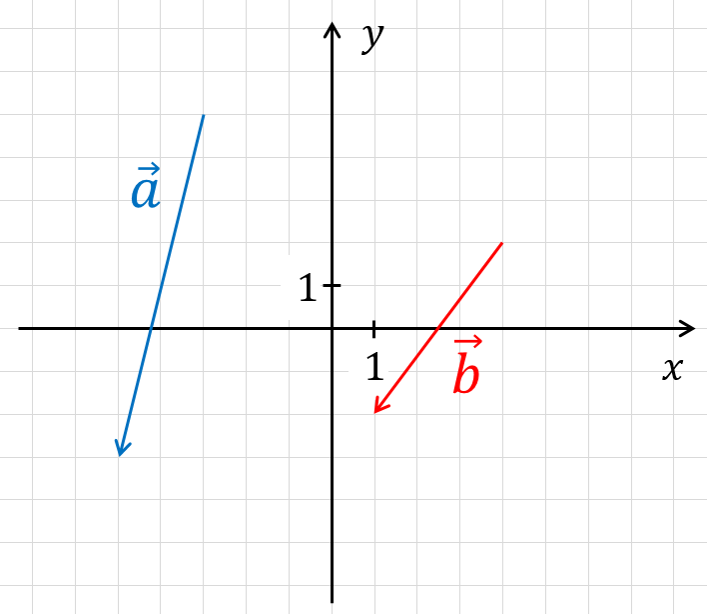
На координатной плоскости изображены векторы ${{a}↖{→}}$ и ${{b}↖{→}}$. Найдите скалярное произведение ${{a}↖{→}}$ и $2{{b}↖{→}}$
Решение
Определим по рисунку координаты векторов.
${{a}↖{→}}\{-2; -8\}$ и ${{b}↖{→}}\{-3; -4\}$
Найдем скалярное произведение ${{a}↖{→}}∙$$2{{b}↖{→}}$:
${{a}↖{→}}∙$$2{{b}↖{→}}$= ${x_a}∙2{x_b}+{y_a}∙2{y_b}={-2}∙{(-6)}+{(-8)}∙{(-8)}=76$
Задача 8
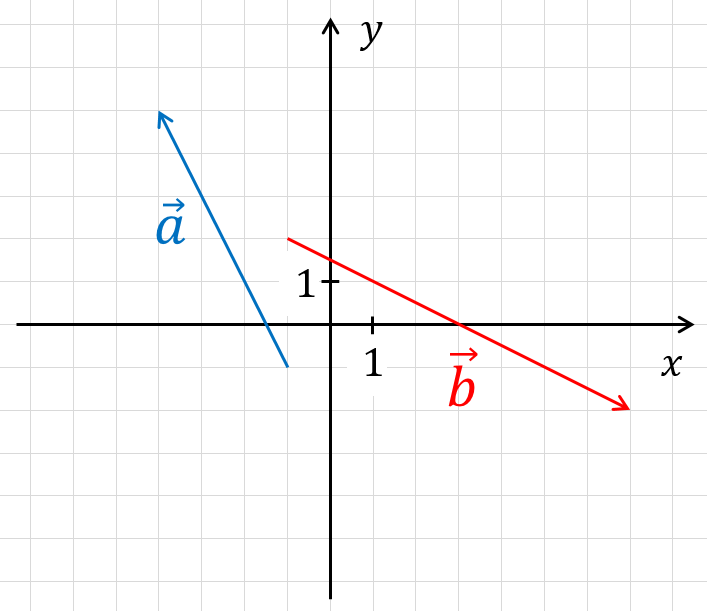
На координатной плоскости изображены векторы ${{a}↖{→}}$ и ${{b}↖{→}}$. Найдите косинус угла между векторами ${{a}↖{→}}$ и ${{b}↖{→}}$
Решение
Определим по рисунку координаты векторов.
${{a}↖{→}}\{-3; 6\}$ и ${{b}↖{→}}\{8; -4\}$
Вычислим косинус искомого угла $\cos∠({{a}↖{→}},{{b}↖{→}})={{{a}↖{→}}⋅ {{b}↖{→}}} / {|{{a}↖{→}}|⋅{|{{b}↖{→}}|}}={-3⋅8+6⋅(-4)} / {√ {9+36}⋅√ {64+16}}={-48} / {60}={-0,8}$.
Задача 9
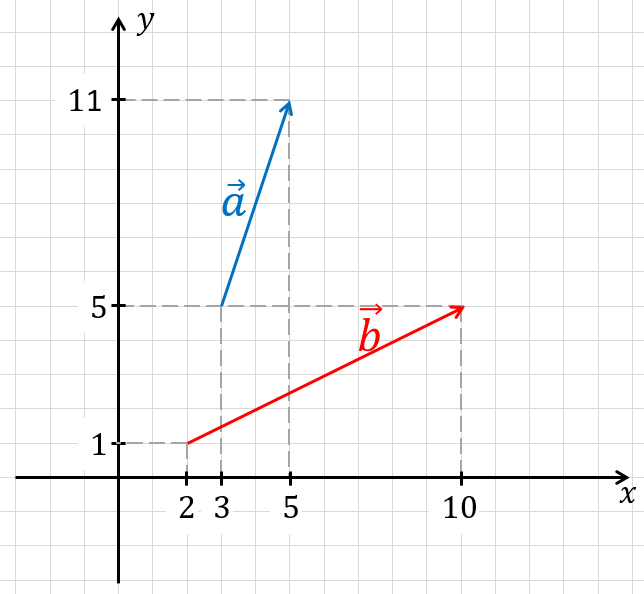
На координатной плоскости изображены векторы ${{a}↖{→}}$ и ${{b}↖{→}}$. Найдите угол между векторами ${{a}↖{→}}$ и ${{b}↖{→}}$. Ответ дайте в градусах.
Решение
Определим по рисунку координаты векторов.
${{a}↖{→}}\{2; 6\}$ и ${{b}↖{→}}\{8; 4\}$
Вычислим косинус искомого угла $\cos∠({{a}↖{→}}, {{b}↖{→}})={{{a}↖{→}}⋅ {{b}↖{→}}} / {|{{a}↖{→}}|⋅{|{{b}↖{→}}|}}={2⋅8+6⋅4} / {√ {4+36}⋅√ {64+16}}={√ 2} / {2}$.
Следовательно, угол между векторами равен 45°
Задача 10
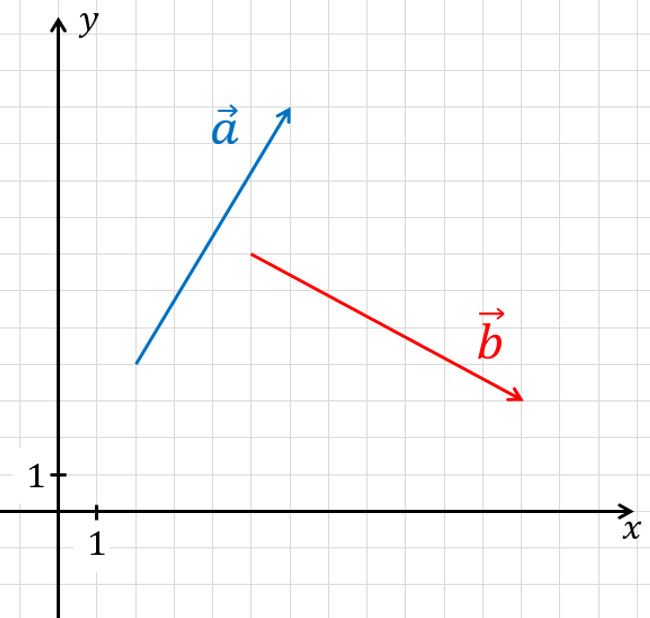
На координатной плоскости изображены векторы ${{a}↖{→}}$ и ${{b}↖{→}}$. Найдите скалярное произведение ${{a}↖{→}}∙$${{b}↖{→}}$
Решение
Определим по рисунку координаты векторов.
${{a}↖{→}}\{4; 7\}$ и ${{b}↖{→}}\{7; -4\}$
Найдем скалярное произведение ${{a}↖{→}}∙$${{b}↖{→}}$:
${{a}↖{→}}∙$${{b}↖{→}}$= ${x_a}∙{x_b}+{y_a}∙{y_b}={4}∙{7}+{7}∙{(-4)}=0$
Задача 11
Найдите длину диагонали прямоугольника, вершины которого имеют координаты $(3; 2)$, $(3; 5$), $(7; 2)$, $(7; 5)$
Решение
Для того, чтобы найти диагональ прямоугольника, найдем длину и ширину:
Заметим, что у нас есть две пары точек, с совпадающими координатами $(3; 2)$, $(3; 5$)$ и $(7; 2)$, $(7; 5)$
$a=5-2=3$
$b=7-3=4$
По теореме Пифагора: (диагональ d является гипотенузой)
$d^2=a^2+b^2=3^2+4^2=25$, тогда $d=5$
Задача 12
Даны векторы ${{a}↖{→}}$$(2;0)$, ${{b}↖{→}}$$(3;4)$. Найдите косинус угла между векторами ${{a}↖{→}}$ и ${{b}↖{→}}$
Решение
Дано: векторы ${{a}↖{→}}$ = $(2; 0)$ и ${{b}↖{→}}$ = $(3; 4)$
Используем формулу для косинуса угла между векторами:
$\cos∠({{a}↖{→}}, {{b}↖{→}})={{{a}↖{→}}⋅ {{b}↖{→}}} / {|{{a}↖{→}}|⋅{|{{b}↖{→}}|}}$.
Скалярное произведение векторов ${{a}↖{→}} = (2; 0)$ и ${{b}↖{→}} = (3; 4)$ равно:
${{a}↖{→}}⋅{{b}↖{→}} = 2⋅ 3 + 0⋅ 4 = 6$.
Длины векторов находим по формуле: ${{|c|}↖{→}}$=$√{x^2+y^2}$
$|{{a}↖{→}}|=√{4 + 0}=2$ и $|{{b}↖{→}}|=√{9 + 16}=5$.
Подставляем это в формулу для косинуса:
$\cos∠({{a}↖{→}}, {{b}↖{→}})=6 / {2⋅5}=0,6$.
Задача 13
Даны векторы ${{a}↖{→}}$$(2;5)$, ${{b}↖{→}}$$(3;7)$. Найдите длину вектора $8,1{{a}↖{→}}-5,9$${{b}↖{→}}$
Решение
1. Нам даны векторы ${{a}↖{→}} = (2;5)$ и ${{b}↖{→}} = (3;7)$.
2. Сначала найдём вектор $8{,}1{{a}↖{→}} - 5{,}9{{b}↖{→}}$. Для этого умножим каждый вектор на соответствующий коэффициент:
$8{,}1{{a}↖{→}} = (8{,}1⋅2;\ 8{,}1⋅5) = (16{,}2;\ 40{,}5)$
$5{,}9{{b}↖{→}} = (5{,}9⋅3;\ 5{,}9⋅7) = (17{,}7;\ 41{,}3)$
3. Вычтем из первого полученного вектора второй:
$(16{,}2 - 17{,}7;\ 40{,}5 - 41{,}3) = (-1{,}5;\ -0{,}8)$
4. Теперь найдём длину полученного вектора по формуле:
$√{(-1{,}5)^2 + (-0{,}8)^2} = √{2{,}25 + 0{,}64} = √{2{,}89} = 1{,}7$
Ответ: $1{,}7$
/p>
Задача 14
Даны векторы ${{a}↖{→}}$$(3;-4)$, ${{b}↖{→}}$$(-6;b_0)$. Найдите $b_0$ если ${{|b|}↖{→}}$=$2{{|a|}↖{→}}$. Если таких значений несколько, в ответ запишите меньшее из них.
Решение
Формула для нахождения длины вектора: ${{|c|}↖{→}}$=$√{x^2+y^2}$
1). Найдем длину вектора {a}: ${{a}↖{→}}$=$√{3^2+(-4)^2}$=$√{9+16}$=$√{25}$=5
2) Найдем длину вектора {b}: ${{b}↖{→}}$=$√{(-6)^2+(b_0)^2}$=$√{36+(b_0)^2}$
Из условия ${{|b|}↖{→}}$=$2{{|a|}↖{→}}$ составим уравнение:
$√{36+(b_0)^2}$=2∙5
$√{36+(b_0)^2}$=10
$36+(b_0)^2=100$
$(b_0)^2=64$
$b_0=±8$
Если таких значений несколько, в ответ запишите меньшее из них, значит $b_0=-8$
Задача 15
Даны векторы ${{a}↖{→}}$$(5;-2)$, ${{b}↖{→}}$$(-1;4)$. Найдите скалярное произведение векторов $1,2{{a}↖{→}}$ и $0,3$${{b}↖{→}}$
Решение
1). Найдем координаты вектора $1,2{{a}↖{→}}$:
$1,2{{a}↖{→}}$ =$(1,2·x_{a};1,2·y_{a})=(1,2·5;1,2·(-1))=(6;-2,4)$
2). Найдем координаты вектора $0,3$${{b}↖{→}}$:
$0,3$${{b}↖{→}}$=$(0,3·x_{b};0,3·y_{b})=(0,3·(-1);0,3·4)=(-0,3;1,2)$
3). Найдем скалярное произведение $1,2{{a}↖{→}}∙$$0,3{{b}↖{→}}$:
$1,2{{a}↖{→}}∙$$0,3{{b}↖{→}}$= ${1,2x_a}∙{0,3x_b}+{1,2y_a}∙{0,3y_b}={6}∙{(-0,3)}+{(-2,4)}∙{(1,2)}=-4,68$
Задача 16
Даны векторы ${{a}↖{→}}$$(-15;1)$, ${{b}↖{→}}$$(-8;2)$ и ${{c}↖{→}}$$(-3;2)$. Найдите длину вектора ${{a}↖{→}}-$${{b}↖{→}}-$${{c}↖{→}}$
Решение
1). Найдем координаты вектора ${{a}↖{→}}-$${{b}↖{→}}-$${{c}↖{→}}$= $({x_a}-{x_b}-{x_c};{y_a}-{y_b}-{y_c})=({-15}-{(-8)}-{(-3)};{1}-{2}-{2})=({-4};{-3})$
2). Найдем длину вектора по формуле: ${{|d|}↖{→}}$=$√{x^2+y^2}$=$√{(-4)^2+(-3)^2}=√{16+9}=√25=5$
Задача 17
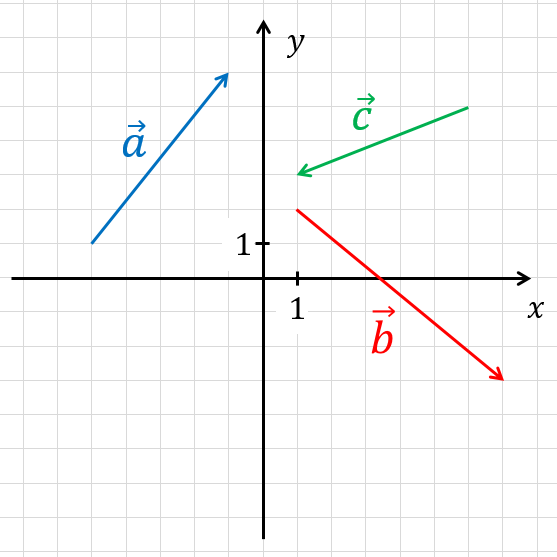
На координатной плоскости изображены векторы ${{a}↖{→}}$, ${{b}↖{→}}$ и ${{c}↖{→}}$. Найдите скалярное произведение $({{a}↖{→}}+$${{b}↖{→}})∙$${{c}↖{→}}$
Решение
Определим по рисунку координаты векторов.
${{a}↖{→}}\{4; 5\}$, ${{b}↖{→}}\{6; -5\} и {{c}↖{→}}\{-5; -2\}$
Найдем сумму векторов ${{a}↖{→}}+$${{b}↖{→}}$= $({x_a}+{x_b};{y_a}+{y_b})=({10};{0})$
Найдем скалярное произведение $({{a}↖{→}}+$${{b}↖{→}})∙$${{c}↖{→}}$= ${x_{a+b}}∙{x_c}+{y_{a+b}}∙{y_c}={10}∙{(-5)}+{0}∙{(-2)}=-50$
Задача 18
Даны векторы ${{a}↖{→}}$$(1;2)$, ${{b}↖{→}}$$(-3;6)$ и ${{c}↖{→}}$$(4;-2)$. Найдите длину вектора ${{a}↖{→}}-$${{b}↖{→}}+$${{c}↖{→}}$
Решение
Даны векторы ${{a}↖{→}} = (1; 2)$, ${{b}↖{→}} = (-3; 6)$ и ${{c}↖{→}} = (4; -2)$. Найдем длину вектора ${{a}↖{→}} - {{b}↖{→}} + {{c}↖{→}}$.
Вычислим координаты результирующего вектора:
${{a}↖{→}} - {{b}↖{→}} + {{c}↖{→}} = (1; 2) - (-3; 6) + (4; -2)$.
По правилам операций над векторами:
${(1 - (-3) + 4; 2 - 6 - 2) = (1 + 3 + 4; 2 - 6 - 2) = (8; -6)}$.
Найдем длину вектора ${(8; -6)}$:
Длина вектора вычисляется по формуле ${|v| = \√{x^2 + y^2}}$, где ${x}$ и ${y}$ — координаты вектора.
Подставляем значения:
${|(8; -6)| = \√{8^2 + (-6)^2} = \√{64 + 36} = \√{100} = 10}$.
Ответ: ${10}$.
Рекомендуемые курсы подготовки

- Получишь все формулы, которые нужны для решения ЛЮБОЙ задачи по теории вероятностей в ЕГЭ по профилю
- Научишься решать задачи №4.5 в ЕГЭ по профилю
- Улучшить свой результат на +15 вторичных баллов
на бесплатном курсе Турбо ЕГЭ

