Задание 16. Физика атомного ядра. ЕГЭ 2026 по физике
Средний процент выполнения: 79.3%
Ответом к заданию 16 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
На какой энергетический уровень нужно перейти электрону в атоме с 3-го энергетического уровня, чтоб при этом испустить фотон c наименьшей частотой? Укажите номер уровня.
Решение
Чем меньше частота фотона, тем меньше энергии мы должны испустить. То есть перейти на ближайший энергетический уровень, то есть второй
Задача 2
На какой энергетический уровень можно перейти с 3, поглотив при этом фотон c наибольшей длинной волны? Укажите номер уровня.
Решение
Чем больше длинна волны, тем меньше получаемая энергия, что значит, что мы поднимемся на ближайший энергетический уровень, с наименьшей полученной энергией. А это есть 4
Задача 3
Сколько процентов ядер некоторого радиоактивного элемента распадётся через время, равное трём периодам полураспада этого элемента? Ответ выразите в (%).
Решение
Дано:
$t=3T$
$(1-{N(3T)}/{N_0})·100%-?$
Решение:
Согласно закону радиоактивного распада, от первоначального количества радиоактивных ядер $N_0$ к моменту времени $t$ должно остаться примерно $N(t)=N_0·2^{-{t}/{T}}$, где $T$ - период полураспада. Следовательно, к моменту времени $t=3T$ ядер останется приблизительно: ${N(3T)}/{N_0}=2^{-{t}/{T}}=2^{-{3T}/{T}}=2^{-3}={1}/{8}$ или в процентах ${N(3T)}/{N_0}·100%={100%}/{8}=12.5%$. Значит, распадется: $(1-{N(3T)}/{N_0})·100%=(1-0.125)·100%=87.5%$
Задача 4
Укажите недостающее обозначение (нейтрон, протон, электрон, альфа-частица) ядерной реакции: $↙{3}↖{7}Li + ↙{1}↖{2}H → {}↙{4}↖{8}Be + X$. Ответ запишите словом (словами).
Решение
$↙{3}↖{7}Li+{}↙{1}↖{2}H→{}↙{4}↖{8}Be+{}↙{Z}↖{A}X$. Найдем массовое $A$ и зарядовое $Z$ числа элемента $X$ и на их основе сделаем вывод: $A=7+2-8=1, Z=3+1-4=0$. Значит, неизвестным элементом является нейтрон $↙{0}↖{1}n$.
Задача 5
Определите элемент, получившийся в ходе α-распада. $↙{92}↖{235}U → {}↙{Z}↖{A}X + {}↙{2}↖{4}He$. В ответе напишите название элемента
Решение
Запишем ядерную реакцию:
$↙{92}↖{235}U→{}↙{90}↖{231}Th+{}↙{2}↖{4}He$ - по таблице Менделеева определим элемент.
Задача 6
Работа выхода материала пластины равна 2 эВ. Чему равна энергия фотонов падающего света, если запирающее напряжение равно 1,5 В? Ответ выразите в (эВ).
Решение
По уравнению Эйнштейна для фотоэффекта $hυ=A_{вых}+U_зe$;
$U_зe=1.5 В ·1.6·10^{-19}Кл=1.5 ·1.6·10^{-19}Дж=1.5 эВ$
$hυ=2эВ+1.5эВ=3.5B$.
Задача 7
Период полураспада ядер радиоактивного изотопа йода-134 равен 54 минутам. Через какое время распадётся 75% ядер в исследуемом образце? Ответ выразите в (мин).
Решение
Дано:
$T=54$мин
$t-?$
${m_0}/{4}=m$
Решение:
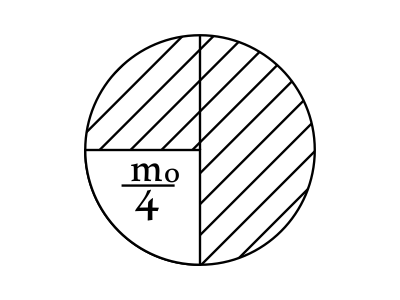
$t=2·T=54·2=108$ мин.
Задача 8
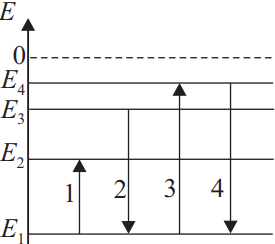
На рисунке представлена диаграмма энергетических уровней атома. Переход с излучением фотона наибольшей частоты изображён стрелкой...
Решение
Квант энергии излучается при переходе на более низкий уровень. При этом расстояние между уровнями пропорционально частоте: $∆E=hυ$. Из диаграммы видно, что среди предложенных вариантов ответа максимальному расстоянию между уровнями, а знчит, и наибольшей частоте излученного кванта соответствует переход с уровня 4 на уровень 1.
Задача 9
Чему равна энергия фотона, имеющего в вакууме длину волны 0,72 мкм? Ответ округлите до десятых. Ответ выразите в (эВ).
Решение
Дано:
$h=6.626·10^{-34}$Дж·с
$с=3·10^8$м/с
$λ=0.72·10^{-6}$м
$E-?$
Решение:
Энергия фотона равна: $E=hυ={hc}/{λ}$(1), где $h$ - постоянная Планка, где $c$ - скорость света в вакууме.
Из (1) найдем $E$: $E={6.626·10^{-34}·3·10^8}/{0.72·10^{-6}}={2.76·10^{-19}}/{1.6·10^{-19}}=1.725=1.7$эВ.
Задача 10
Радиоактивный изотоп технеция $↙{43}↖{95}Tc$, не обнаруженный в природе, был получен искусственно в результате реакции $↙{42}↖{94}Mo + ↙{1}↖{2}H → {}↙{43}↖{95}Tc + X$. Какая частица (нейтрон, протон, электрон, альфа-частица) выбрасывается? Ответ запишите словом (словами).
Решение
$↙{42}↖{94}Mo+{}↙{1}↖{2}H→{}↙{43}↖{95}Tc+X$. Найдем массовое $A$ и зарядовое $Z$ числа элемента $X$ и на их основе сделаем вывод: $A=94+2-95=1, Z=42+1-43=0$. Значит, неизвестным элементом является нейтрон $↙{0}↖{1}n$.
Задача 11
Период полураспада нептуния 2,3 суток. Через какое время количество радиоативных атомов уменьшится в 4 раза? В ответе запишите через сколько суток.
Решение
Дано:
$T-2.3$суток
${m_0}/{4}∼t-?$
Решение:
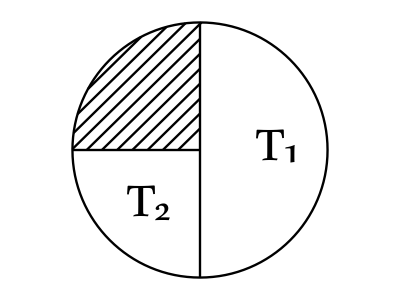
Для определения ответа построим схему. Через 2 периода полураспада $2·T=2·2.3=4.6$суток.
Задача 12
Определите число нейтронов в изотопе ядра $↙{92}↖{235}U$.
Решение
У изотопа ядра $↙{92}↖{235}U$: число протонов равно $Z=92$ - зарядовое число; число нуклонов (протонов - Z и нейтронов - N) равно $A=235$ - массовое число. Тогда из $A=Z+N, N=A-Z=235-92=143$.
Задача 13
Атом водорода, поглощая фотон с частотой ν = 2,94 · 1015 Гц, переходит из основного состояния в возбуждённое. Найдите максимальную длину волны, которую может излучать атом. Энергию электрона на n-ом уровне атома водорода можно представить в виде $E_n = -{hR}/{n^2}$. $h=6.62·10^{-34}$Дж. Постоянная Ридберга R = 3,29 · 1015 c−1. Ответ выразите в (нм).
Решение
Дано:
$υ=2.94·10^{15}$
$E_r=-{h·R}/{n^2}$
$R=3.29·10^{15}$
$h=6.62·10^{-34}$Дж/с
$λ-?$
Решение:
$E_{вод}=-{h·R}/{r^2}+hυ$ - энергия водорода в возбужденном состоянии равна сумме энергий основного состояния и фотона.
$λ={hc}/{E_{вод}}={hc}/{-{h·R}/{r^2}+hυ}(n=1)={6.62·10^{-34}·3·10^8}/{-{6.62·10^{-34}·3.29·10^{15}}/{r^2}+6.62·10^{-34}·2.54·10^{15}}=857·10^{-9}=857$нм
Задача 14
Чему равен импульс фотона, если соответствующая длина волны равна 600 нм? $h=6.62·10^{-34}$. Ответ выразите в (·10−27 кг·м/с) и округлите до десятых
Решение
Дано:
$λ=600·10^{-9}м$
$p↖{→}-?$
Решение:
$p↖{→}={hυ}/{c}={h}/{λ}={6.62·10^{-34}}/{600·10^{-9}}=1.1·10^{-27}$.
Задача 15
Ядро некоторого элемента состоит из 83 протонов и 131 нейтрона. Сколько нейтронов будет содержаться в ядре, образовавшемся из исходного после испускания одной α-частицы и трёх β-частиц?
Решение
Запишем уравнение данной реакции: $↙{83}↖{214}X-{}↙{2}↖{4}α-3{}↙{-1}↖{0}β→{}↙{Z}↖{A}Y$, где $X$ - исходный элемент, $Y$ - образовавшийся элемент. Найдем зарядовое число элемента $Y$: $Z=83-2-3·(-1)=83-2+3=84$. Найдем массовое числоэлемента $Y$: $A=214-4-3·0=210$. Тогда число нейтронов $N$ в ядре элемента $Y$ равно: $N=A-Z=210-84=126$.
Задача 16
Какой заряд Z будет иметь ядро элемента, получившееся из ядра изотопа $↙{92}↖{238}U$ после трёх α-распадов и одного β-распада?
Решение
Решение:
$↙{92}↖{238}U⇄{}↙{Z}↖{A}x+3{}↙{2}↖{4}He+{}↙{-1}↖{0}e$,
$Z=92-3*2-(-1)=87$
Задача 17
Изначально некоторого радиоактивного изотопа было 400 г. Через 7,8 лет его стало 100 г. Каков период полураспада данного элемента? Ответ выразите в годах.
Решение
Дано:
$m_0=0.4$кг
$m=0.1$кг
$t=7.8$лет
$T-?$
Решение:
Согласно закону радиоактивного распада, по истечении времени от первоначальной массы радиоактивного изотопа $m_0$ останется примерно $m=m_0·2^{-{t}/{T}}$ или $m={m_0}/{2^{{t}/{T}}}$ или $2^{{t}/{T}}={m_0}/{m}$ или $2^{{t}/{T}}={0.4}/{0.1}$
$2^{{t}/{T}}=4⇒2^{{t}/{T}}=2^2⇒{t}/{T}=2⇒T={t}/{2}={7.8}/{2}=3.9$ года(лет).
Задача 18
Определите массовое и зарядовое числа продукта реакции $↙{7}↖{14}N + ↙{0}↖{1}n → ↙{6}↖{14}C + X$.
| Массовое число | Зарядовое число |
Решение
Дано:
$↙{7}↖{14}N+{}↙{0}↖{1}n→{}↙{6}↖{14}C+X$
$A-?X-?$
Решение:
Воспользуемся законом сохранения заряда: $Z=7+0-6=1$.
Воспользуемся законом сохранения массового числа: $A=14+1-14=1$.
Задача 19
Какой частоты свет следует направлять на поверхность вольфрама, чтобы максимальная скорость фотоэлектронов была равна 10^6 м/c? Работа выхода электрона из вольфрама 4,5 эВ. $h={6.6·10^{-34}}$. Ответ округлите до сотых. Ответ выразите в (·1015 Гц).
Решение
Дано:
$υ_{max}=10^6$м/c
$А_{вых}-?$
$v-?$
Решение:
По уравнению фотоэффекта: $hv=А_{вых}+{mυ_{max}^2}/{2}$
$v={А_{вых}+0.5·m·υ_{max}^2}/{h}={4.5·1.6·10^{-19}+0.5·9.1·10^{-31}·10^{12}}/{6.6·10^{-34}}=1.78·10^{15}$Гц.
Задача 20
В результате ядерной реакции $↙{13}↖{27}Al +↙{0}↖{1}n → ? +↙{2}↖{4}He$ был получен химический элемент X. Укажите число нуклонов и протонов в ядре образовавшегося химического элемента.
Решение
Решение:
Запишем уравнение ядерной реакции:
$↙{13}↖{27}Al+{}↙{0}↖{1}n⇄{}↙{11}↖{24}x+{}↙{2}↖{4}He$.
Тогда число нуклонов $A=24$, а число протонов $Z=11$.
Рекомендуемые курсы подготовки

- На этом интенсиве ты 100000% поймешь, что такое магнитное поле и как его применяют в физике
- Вместе со мной разберешь все возможные варианты задач на тему Магнетизм и научишься решать задачи С-части, за которые дают целых 3 первичных балла(это около 6-10 вторичных за одну задачу)
- Научишься пользоваться правилами рук и Ленца
- Без проблем будешь определять разницу между магнитным и эл. полем
- Сможешь юзать 80% инфы по правилам правой и левой руки в ЕГЭ
- Научишься решать задания № 14,15,16,17 в тестовой и №26, 28 и 29 в письменной части, которые встречаются каждый год в ЕГЭ, но справитсья с ними не могут
на бесплатном курсе Турбо ЕГЭ

