Задание 7. Анализ графиков и диаграмм. ЕГЭ 2026 по математике (базовой)
Средний процент выполнения: 91.8%
Алгоритм решения задания 7:
Определите, каким способом задана функция: формулой, графиком или таблицей.
Если функция задана графиком, найдите по оси аргументов нужное значение и определите соответствующее значение функции.
При анализе поведения функции обратите внимание на возрастание, убывание и постоянные участки.
Используйте форму графика для установления характерных свойств функции в указанной области.
Сопоставьте полученные данные с условием задания.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
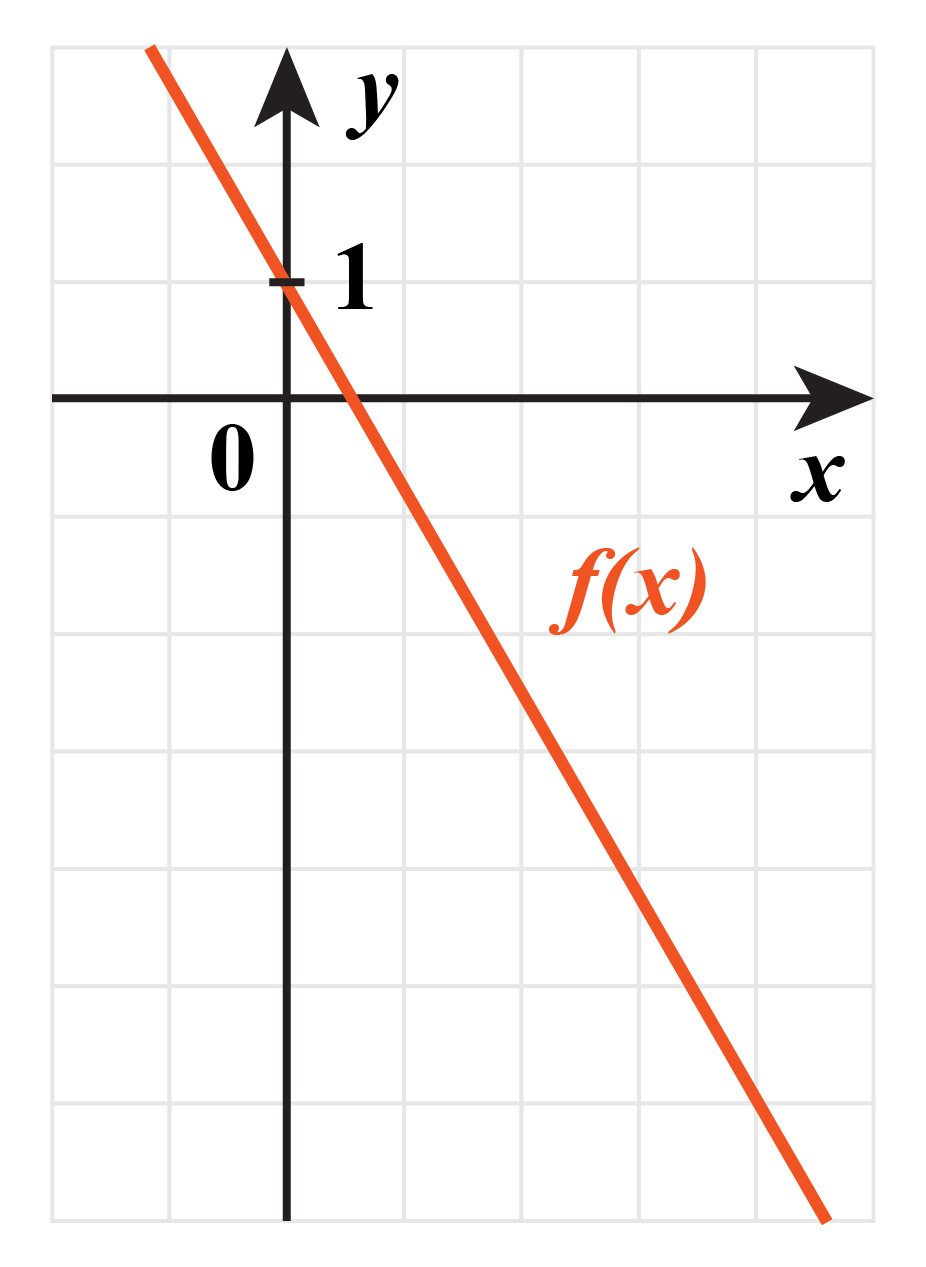
Дана функция $f(x)=kx+b.$ Найдите значение производной функции $f’(x)$ в точке $х=3$
Решение
Значение производной - это тангенс угла наклона к положительной oX. В нашем случае - это тангенс тупого угла. Тогда найдем тангенс смежного с ним острого угла, используя формулу: $tg a=-tg b,$ где $a, b -$ смежные углы. Для того чтобы найти тангенс, нужно достроить до прямоугольного треугольника. Проведя катеты, найдем их длины: противолежащий 7, прилежащий - 4. Тогда тангенс, равный отношению противолежащего катета к гипотенузе, равен $tg a=-tg b=- 7/4=-1,75$.
Задача 2
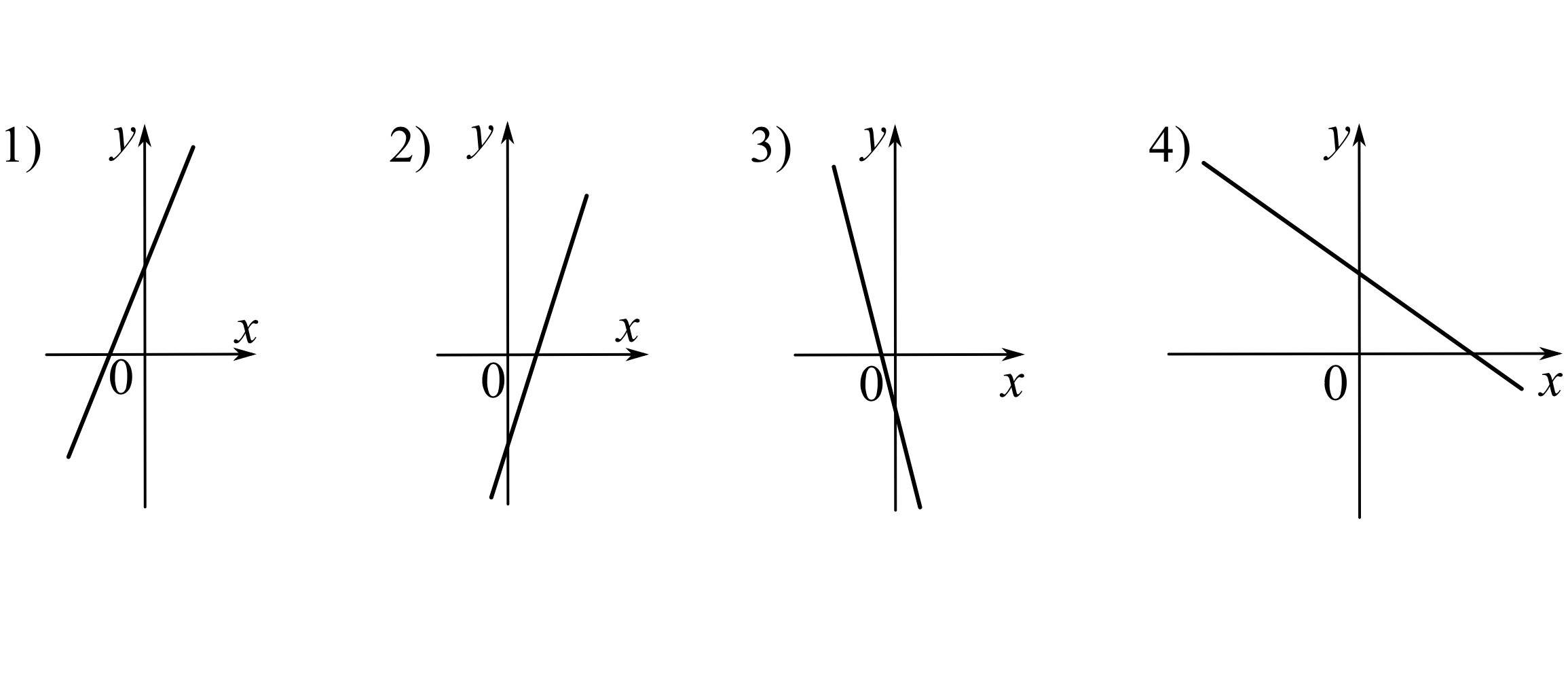
На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
А) k > 0, b < 0
Б) k < 0, b > 0
В) k > 0, b > 0
Г) k < 0, b < 0
В таблице под каждой буквой, соответствующей неравенствам, впишите номер графика функции, знаки коэффициентов которой определены этими неравенствами.
Решение
Для решения задачи вспомним, какой коэффициент за что отвечает. Коэффициент k - угловой коэффициент наклона - отвечает за угол наклона: если k>0, прямая возрастает, если k<0 - прямая убывает. Коэффициент b отвечает за точку пересечния с осью ординат (ось Y): если b>0, ось пересекаем выше нуля, если b<0 - пересекаем ось ниже нуля. Зная это, определим коэффициенты для каждой прямой.
1. Прямая возрастает, значит, k>0. Прямая пересекает oY выше нуля, значит, b>0 - это буква В.
2. Прямая возрастает, значит, k>0. Прямая пересекает oY ниже нуля, значит, b<0 - это буква А.
3. Прямая убывает, значит, k<0. Прямая пересекает oY ниже нуля, значит, b<0 - это буква Г.
4. Прямая убывает, значит, k<0. Прямая пересекает oY выше нуля, значит, b>0 - это буква Б.
Получаем комбинацию А-2, Б-4, В-1, Г-3.
Задача 3
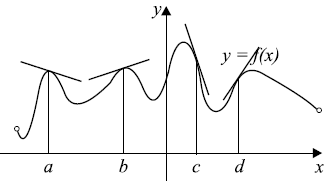
На рисунке изображены касательные к графику функции $y = f(x)$ в точках $a, b, c$ и $d$. Установите соответствие между точками из левого столбца и значениями производной функции $y = f(x)$ в этих точках из правого столбца.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| a b c d | 1) $-3$ 2) $-0,3$ 3) 0,25 4) 2,5 |
Под каждой буквой укажите соответствующий номер.
Решение
Для решения задачи необходимо определить наклон касательной к графику функции в каждой из заданных точек. Значение производной функции в точке соответствует угловому коэффициенту касательной в этой точке.
1. В точке a касательная имеет отрицательный наклон, что соответствует варианту 1 и 2, но при этом прямая медленно убывает, значит, производная по модулю маленькая, что соответствует значению производной $f'(a) = -0,3$, т.е. номеру 2
2. В точке b касательная имеет положительный наклон, что соответствует варианту 3 и 4, но при этом прямая медленно возрастает, значит, производная по модулю маленькая, что соответствует значению производной $f'(b) = 0,25$, что соответствует номеру 3.
3. В точке c касательная имеет крутой отрицательный наклон, равный $f'(c) = -3$, что соответствует номеру 1.
4. В точке d касательная имеет значительный крутой положительный наклон, равный $f'(d) = 2,5$, что соответствует номеру 4.
Ответ: 2314.
Задача 4
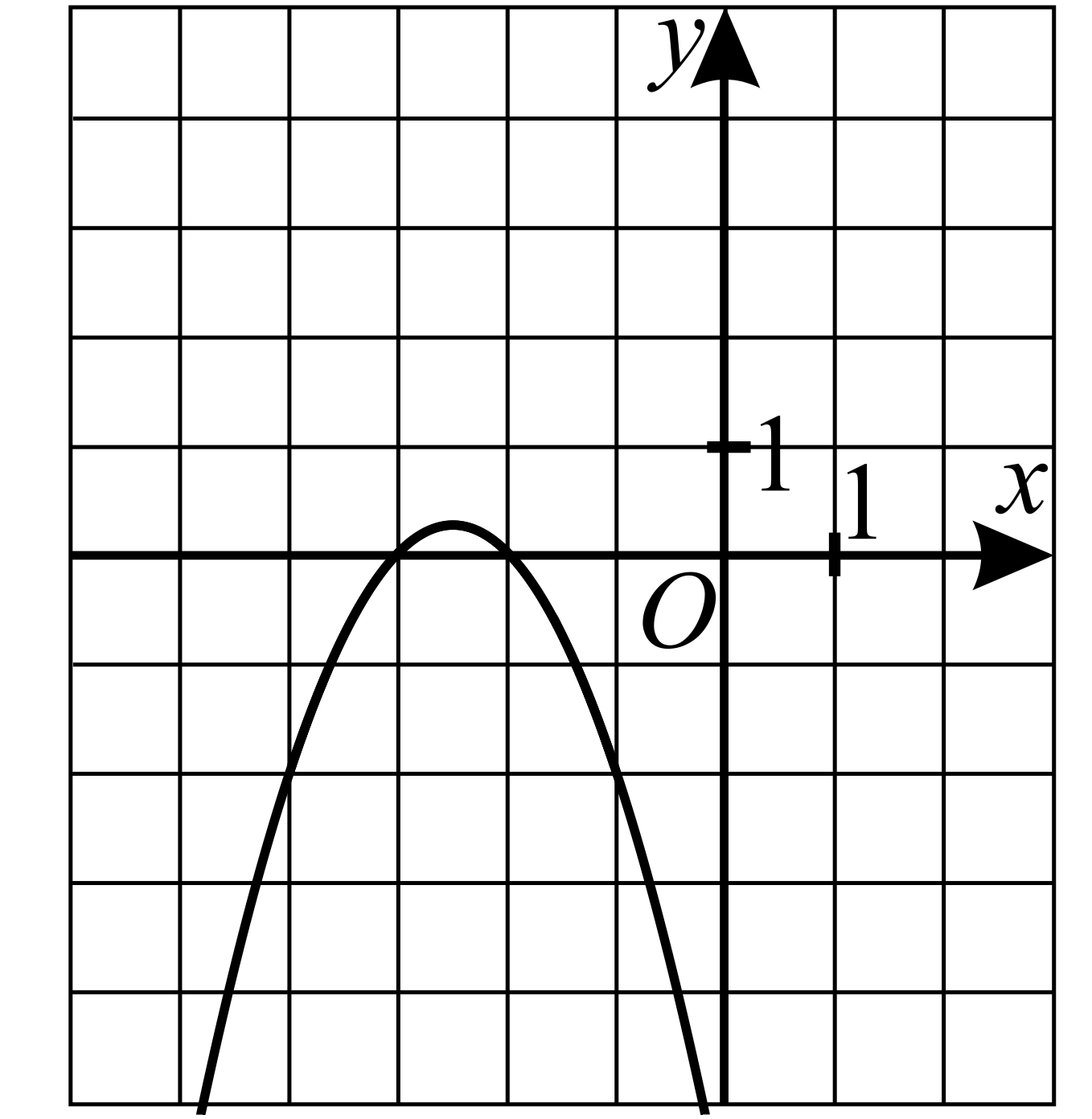
На рисунке изображена функция вида y=ax²+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения справедливы.
УТВЕРЖДЕНИЯ:
А) Функция возрастает на промежутке.
Б) Функция убывает на промежутке.
ПРОМЕЖУТКИ:
1) [−5;−4]
2) [−4;−1]
3) [−4,5;−2]
4) [−2;−0,5]
В таблице под каждой буквой, соответствующей утверждению, впишите номер промежутка, на котором это утверждение справедливо.
Решение
В этой задаче очень важно выбрать промежуток, в котором функция ТОЛЬКО убывает или ТОЛЬКО возрастает! Посмотрим на первый промежуток [-5;-4] - тут наша функция только растет, значит нам подойдет утверждение А. Второй промежуток [-4;-1] - тут функция и возрастает и убывает, никакое утверждение не подходит. Третий промежуток [-4,5; -2] - тут функция и возрастает и убывает, никакое утверждение не подходит. Четвертый промежуток [-2; -0,5] - тут функция только убывает, а значит нам подойдет утверждение Б. Ответ: 14
Задача 5
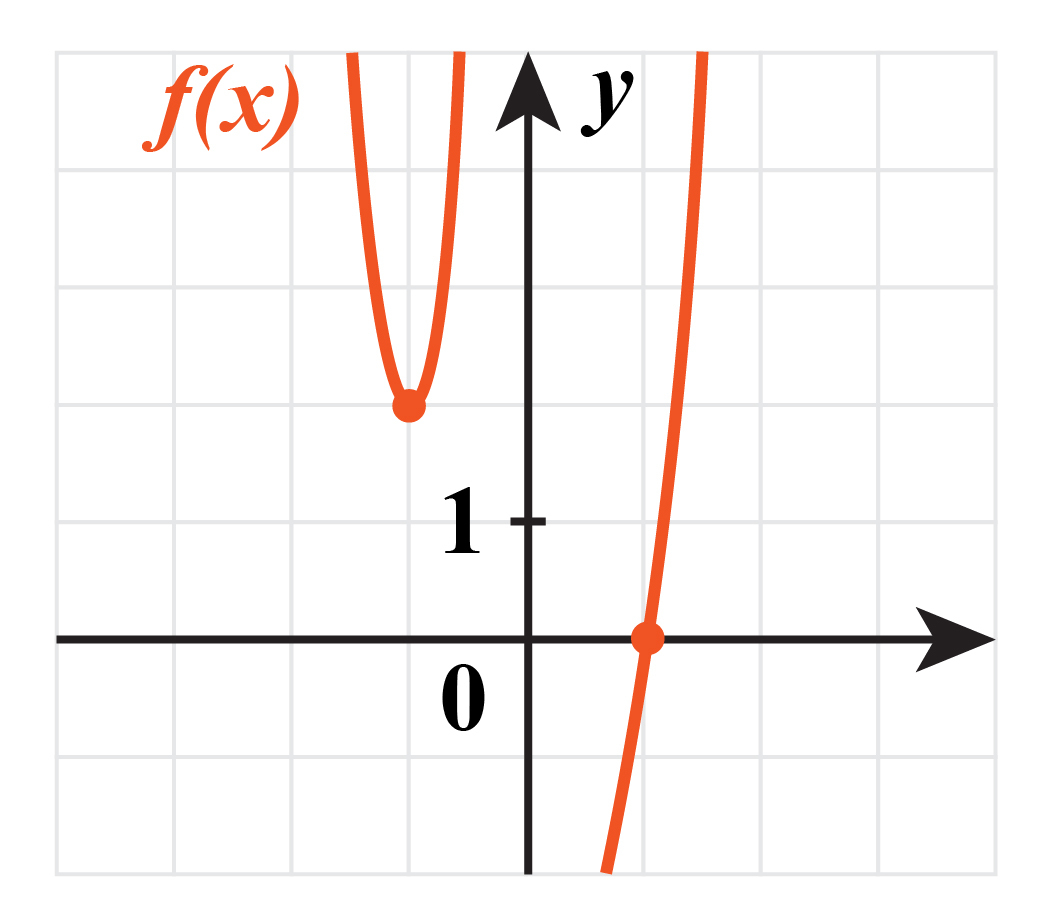
Дана функция $f(x).$ Найдите значение производной функции $f’(x)$ в точке $х=-1.$
Решение
Значение производной - это тангенс угла наклона касательной к положительной oX. В нашем случае - это прямая, параллельная оси абсцисс, посколько она проходит через точку экстремума. Значение производной в точке экстремума равно нулю. Тогда ответ на задачу: 0.
Задача 6
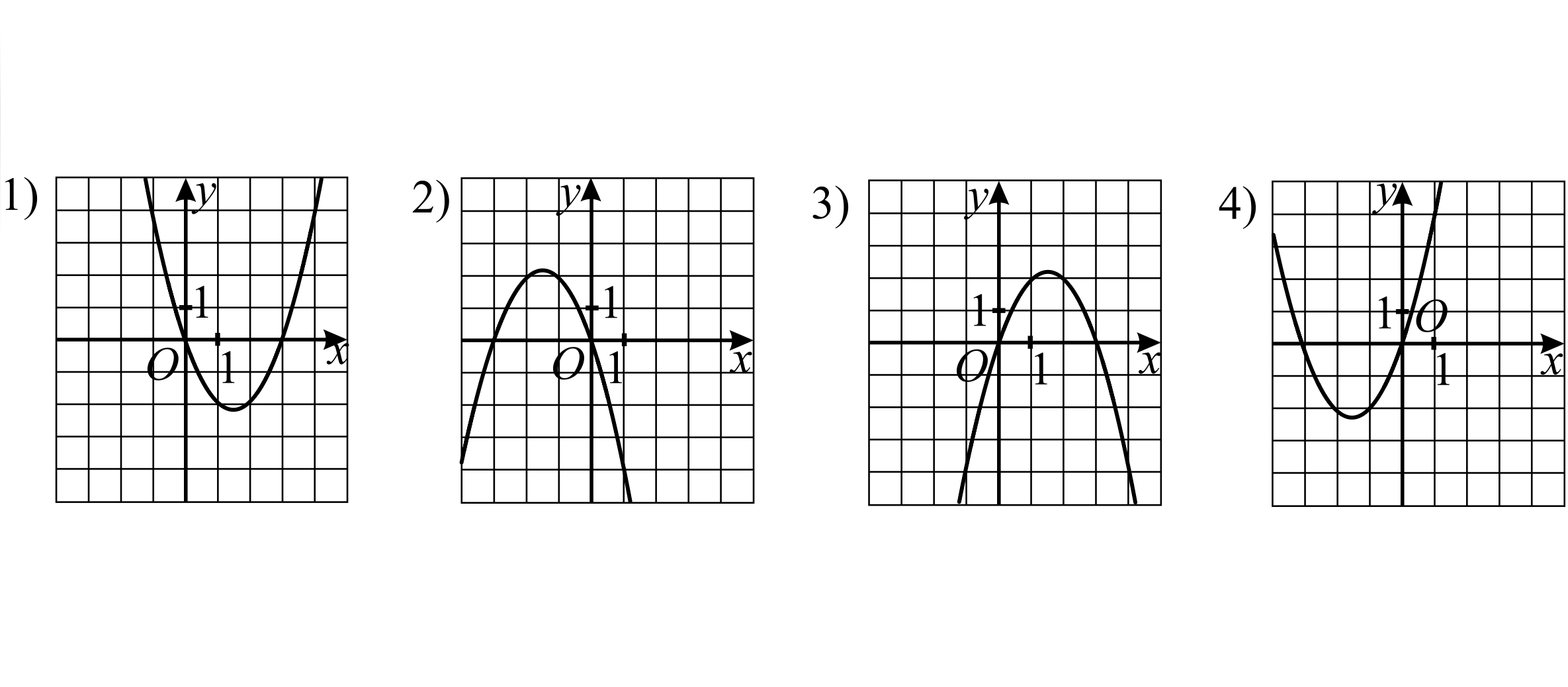
Установите соответствие между функциями и их графиками (см. рис.).
А) y = −x²− 3x
Б) y = −x²+3x
В) y=x²−3x
Г) y=x²+3x
В таблице под каждой буквой, соответствующей формуле, впишите номер графика, который ею задан.
Решение
Функции:
| Буква | Функция |
|---|---|
| А | y = −x² − 3x |
| Б | y = −x² + 3x |
| В | y = x² − 3x |
| Г | y = x² + 3x |
Как определить:
- Если коэффициент при x² положительный - ветви параболы направлены вверх (В и Г)
- Если коэффициент при x² отрицательный - ветви параболы направлены вниз (А и Б)
- Нули функции (точки пересечения с осью x) находятся решением уравнения y=0
Решение:
А) y = −x² − 3x => -х( х+3)=0 => нули: x=0 и x=-3, ветви вниз → График 2
Б) y = −x² + 3x — -х( х-3)=0 => нули: x=0 и x=3, ветви вниз → График 3
В) y = x² − 3x — х( х-3)=0 => нули: x=0 и x=3, ветви вверх → График 1
Г) y = x² + 3x — х( х+3)=0 => нули: x=0 и x=-3, ветви вверх → График 4
Ответ: 2314
Задача 7
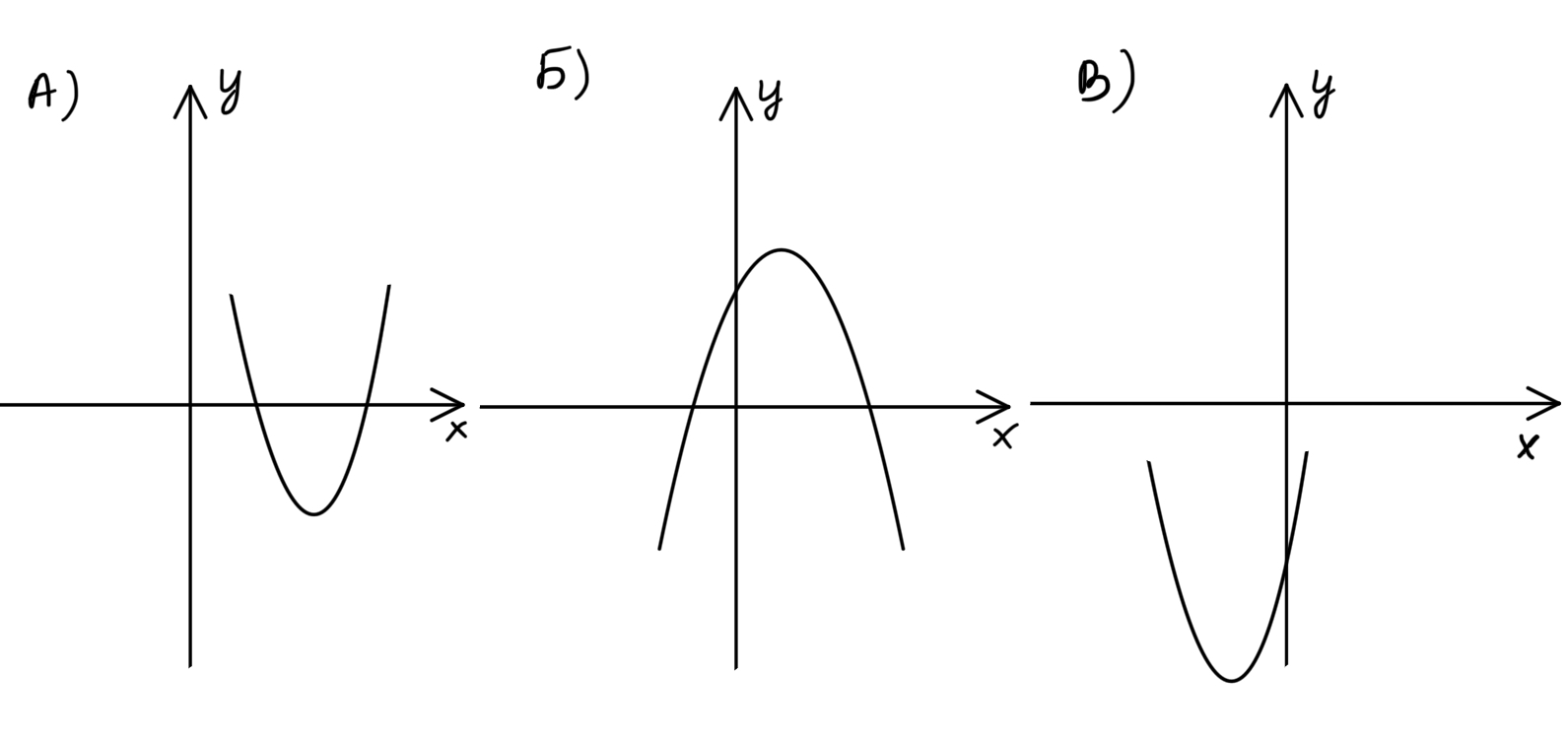
На рисунке изображены графики функций вида y=ax²+bx+c. Установите соответствие между графиками и знаками их коэффициентов а и с.
1) a>0, c<0
2) a>0, c>0
3) a<0, c<0
4) a<0, c>0
В таблице под каждой буквой, соответствующей графикам функции, впишите номера неравенств, определяющих коэффициенты этих функций.
Решение
Ветви вниз, если коэффициент а при x² меньше 0, ветви вверх, если коэффициент а при x² больше 0. Коэффициент с отвечает за точку пересечения с осью ординат. Если над 0, то с>0. Если под 0, то с<0.
Задача 8
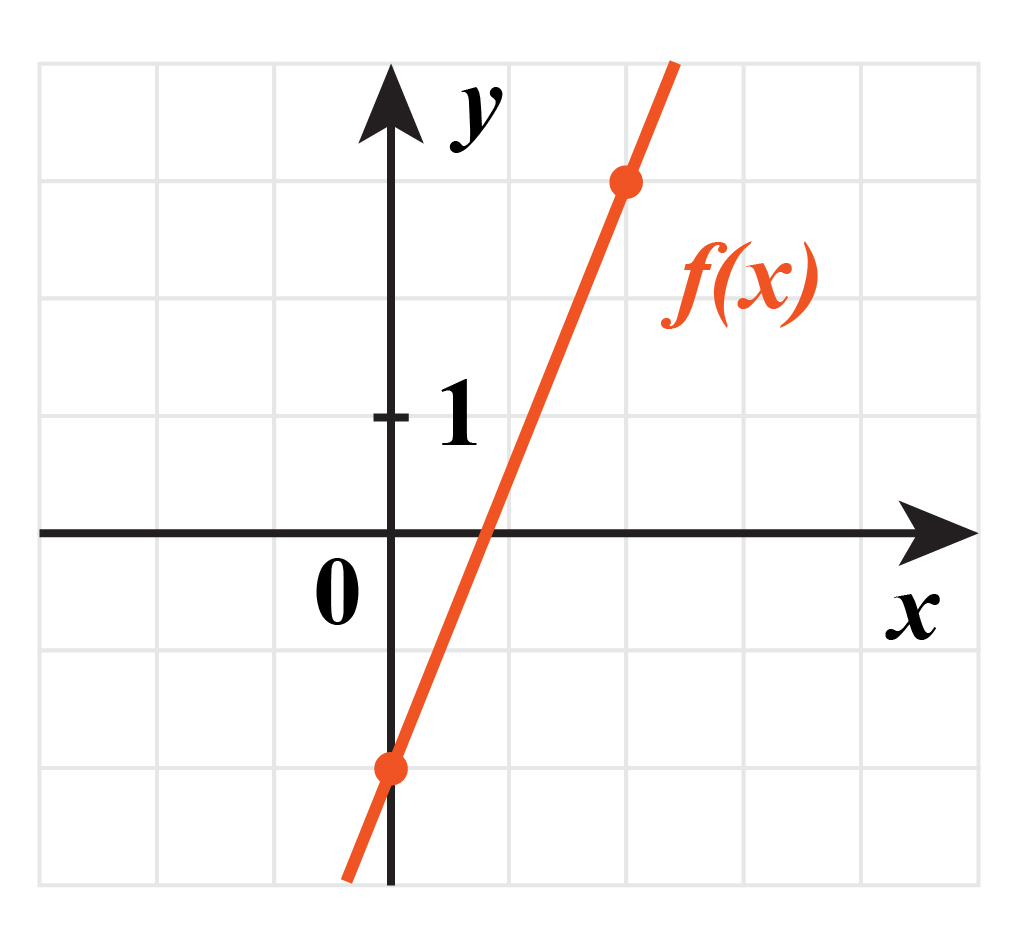
Дана функция $f(x)=kx+b.$ Найдите угловой коэффициент прямой.
Решение
Угловой коэффициент прямой - это тангенс угла наклона к положительной oX. Для того чтобы найти тангенс, нужно достроить до прямоугольноuо треугольника. Проведя катеты, найдем их длины: противолежащий 5, прилежащий - 2. Тогда тангенс, равный отношению противолежащего катета к гипотенузе, равен $k=tg a=5/2=2,5$.
Задача 9
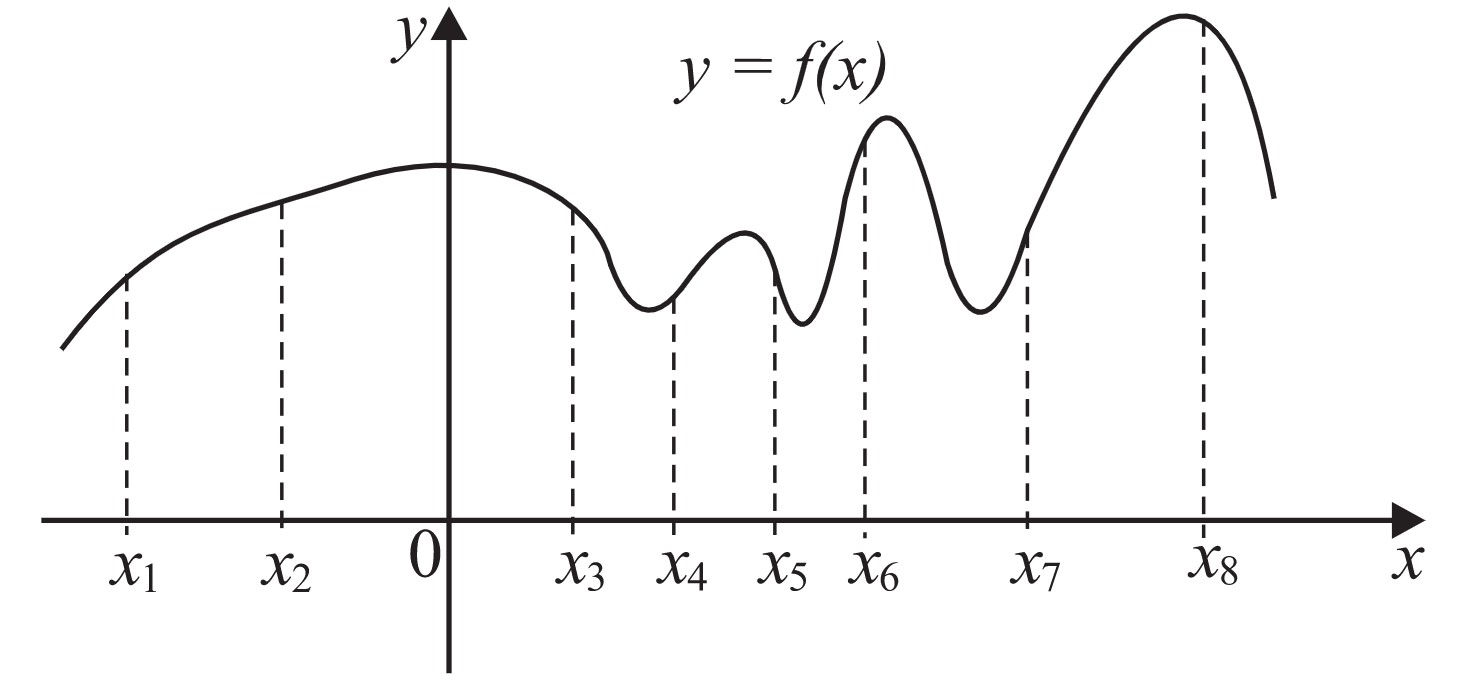
На рисунке изображён график функции $y=f(x)$ и восемь точек на оси абсцисс: $x_1, x_2, x_3, …, x_8$. В скольких из этих точек производная функции $f(x)$ отрицательна?
Решение
Производная отрицательна только в тех точках, которые принадлежат промежуткам убывания функции, если касательные в них не горизонтальны. Таких точек 3: $x_3, x_5, x_8$.
Задача 10
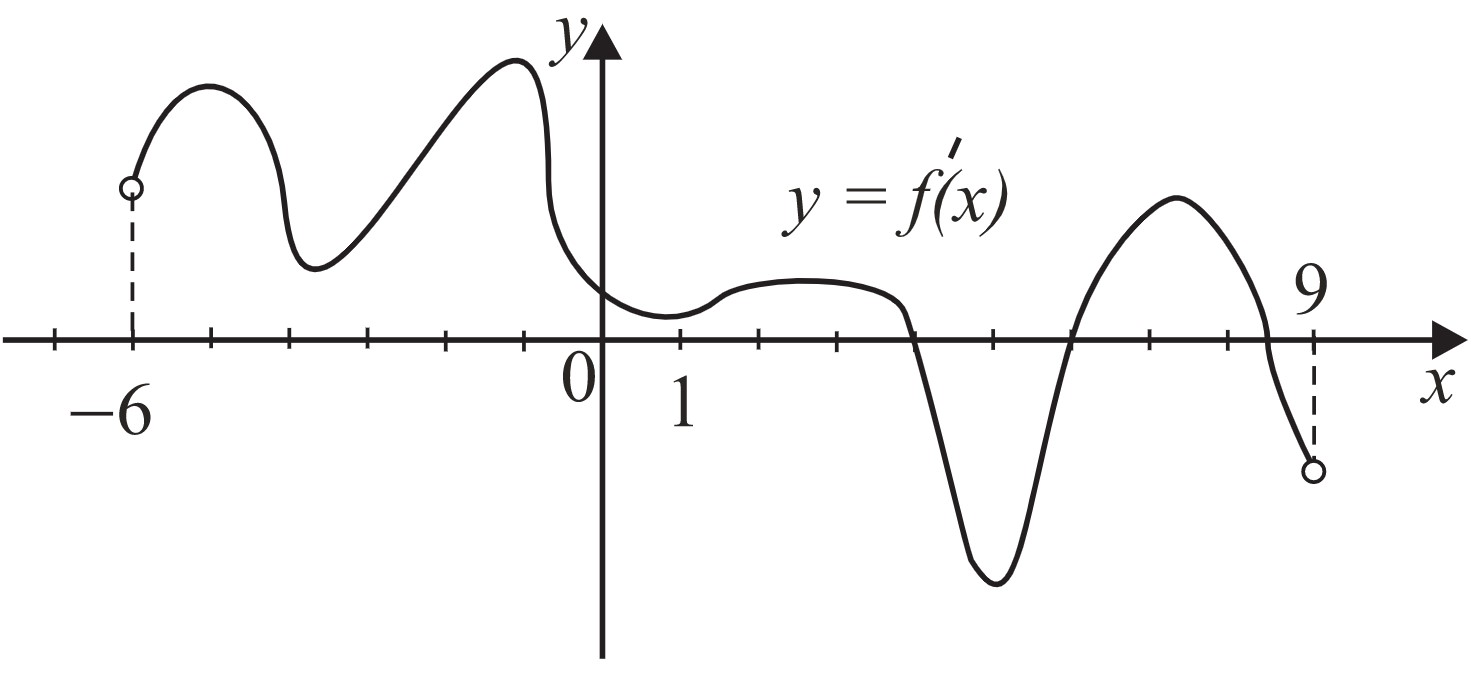
На рисунке изображён график $y=f′(x)$ — производной функции $f(x)$, определённой на интервале (−6;9). Найдите количество точек максимума функции $f(x)$ на заданном интервале.
Решение
Из графика видно, что производная $f′(x)$ функции $f(x)$ равна нулю в трёх точках и только при переходе через две точки $x=4$ и $x_0>8$ $(x_0<9)$ меняет знак с «+» на «−». Поэтому на промежутке (−6;9) ровно 2 точки максимума.
Задача 11
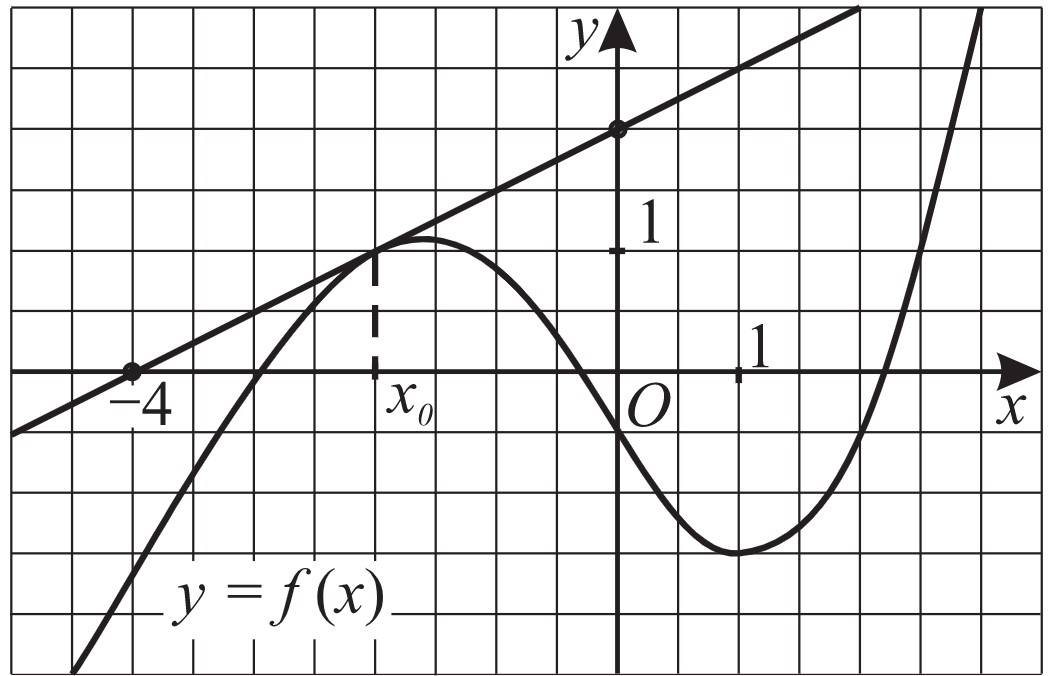
На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение
Используем следующее свойство: $f′(x_0)=k=tgα=2/4=1/2=0,5$
Обратим внимание на то, что $α<90°$. Из этого следует, что $tgα>0$
Задача 12
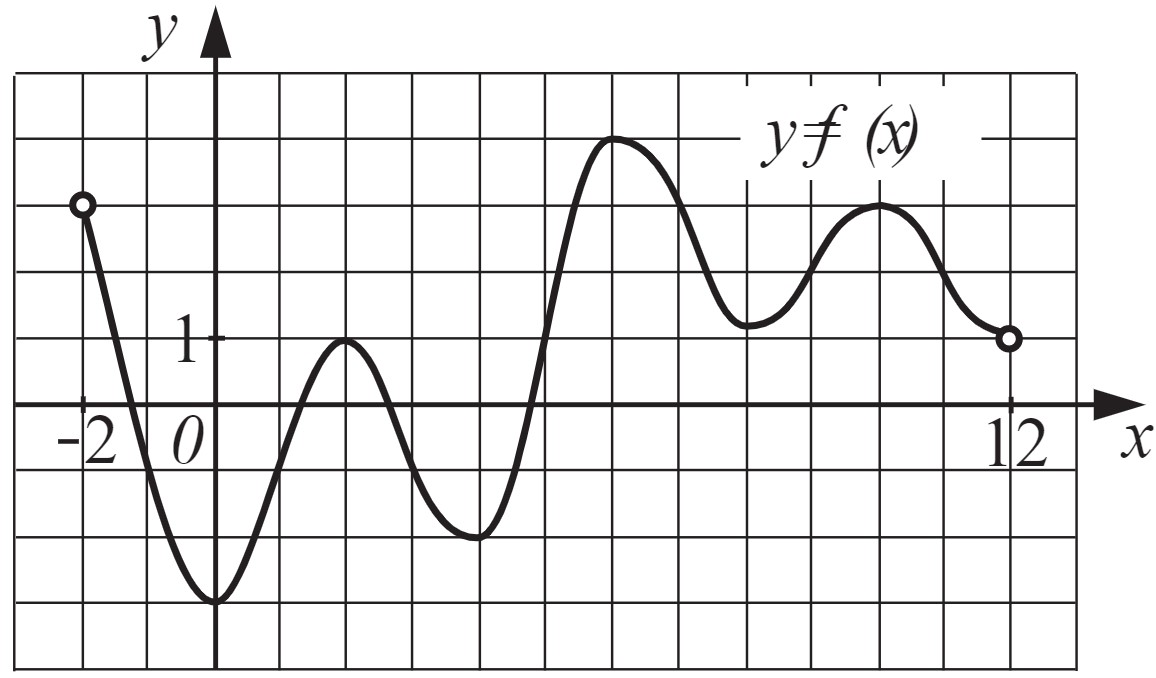
На рисунке изображён график функции, определённой на интервале (−2;12). Найдите сумму точек экстремума функции $f(x)$.
Решение
Точки экстремума - это точки, в которых функция меняет свою монотонность. Для точек максимума - возрастание меняется на убывание, для точек минимума - убывание меняется на возрастание.
$x_{min}=0;4;8; x_{max}=2;6;10$
$0+4+8+2+6+10=30$
Задача 13
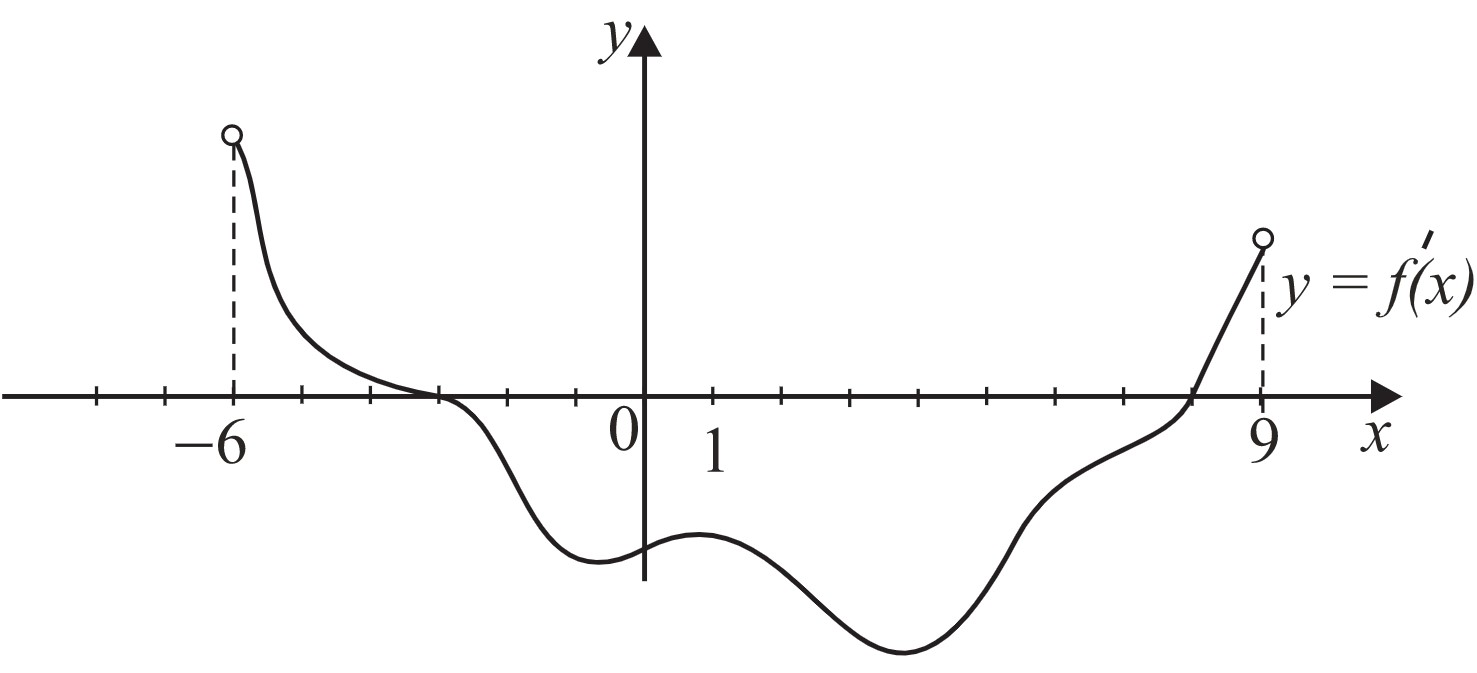
На рисунке изображён график $y=f′(x)$ — производной функции $f(x)$, определённой на интервале $(−6;9)$. Найдите промежутки убывания функции $f(x)$. В ответе укажите длину наибольшего из них.
Решение
Так как на промежутке $(−3;8)$ производная функции $y=f′(x)$ отрицательна, то на этом промежутке функция $y=f(x)$ убывает. Длина этого промежутка равна $8−(−3)=11$.
Задача 14
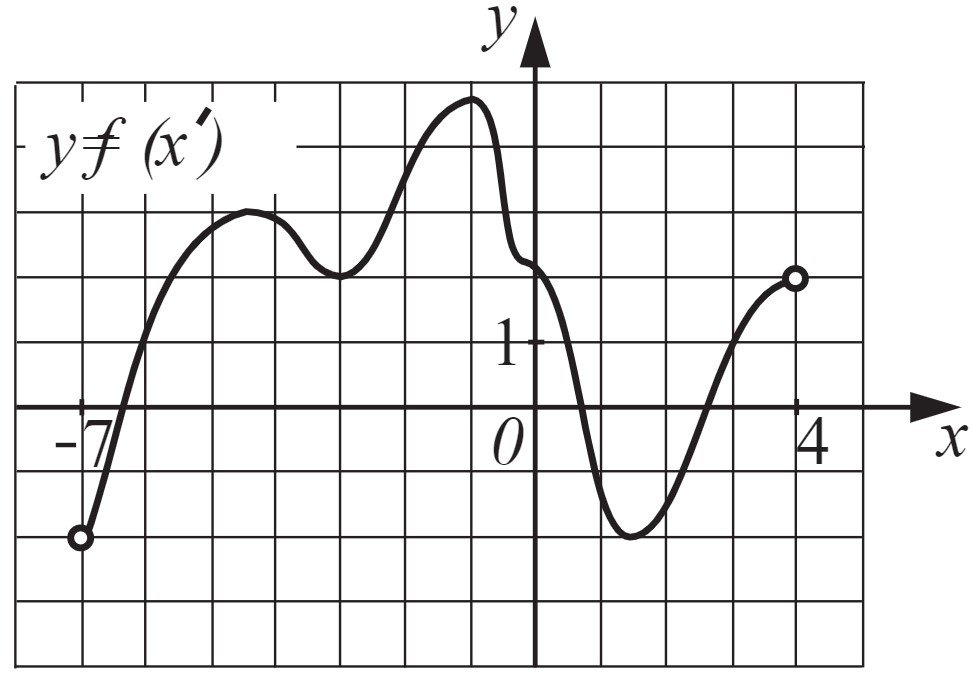
На рисунке изображён график $y=f′(x)$ — производной функции $f(x)$, определённой на интервале (−7;4). Найдите промежутки возрастания функции $f(x)$. В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение
Функция возрастает, значит $f'(x) > 0$, тогда т.к. $x ∈ z$, то $x = {-6; -5; -4; -3; -2; -1; 0; 3}$
их сумма $-6 + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 3 = -18$
Задача 15
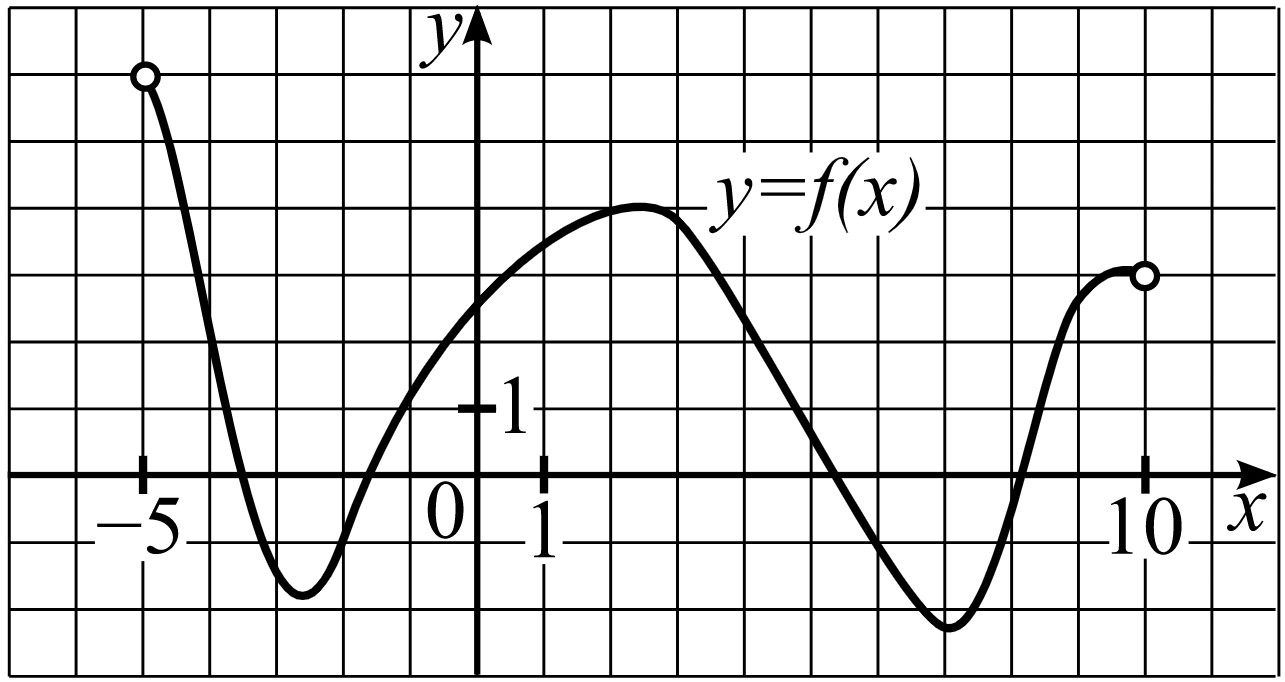
На рисунке изображён график функции $y=f(x)$, определённой на интервале (−5;10). Определите количество целых точек, в которых производная функции положительна.
Решение
$f′(x)>0$ на промежутках, где функция возрастает, количество целых значений, удовлетворяющих условию, то есть $х = {-2;-1;0;1;2;8;9}$ (7 точек)
Задача 16
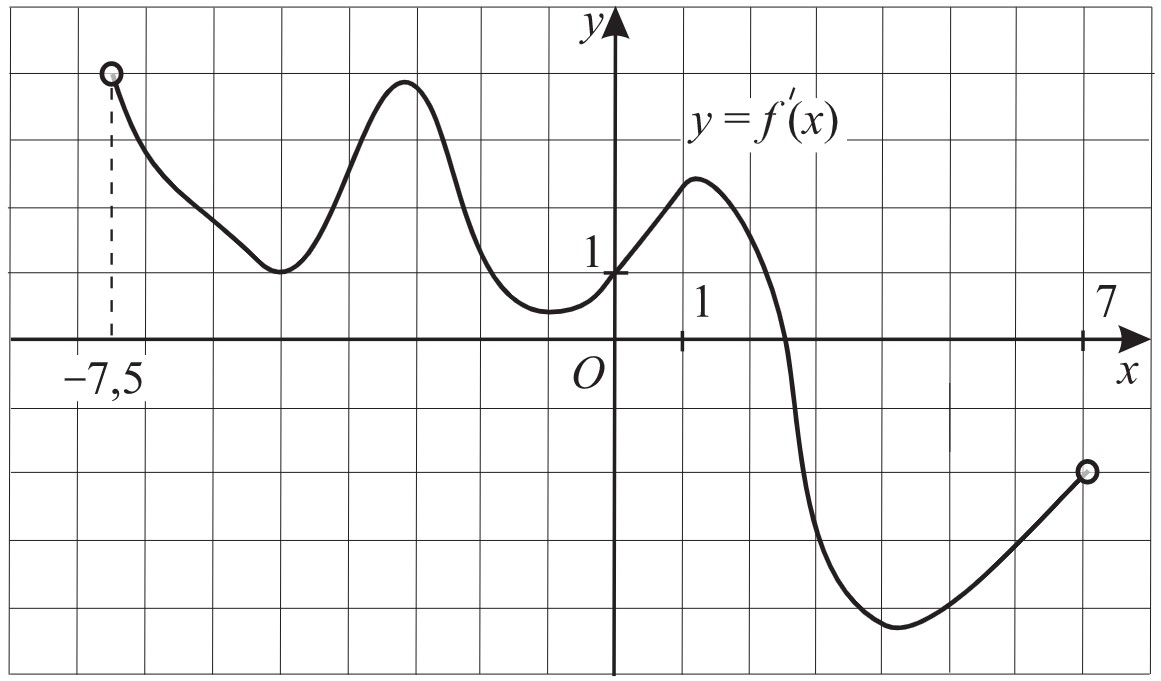
На рисунке изображён график производной функции $y=f′(x)$, определённой на отрезке (−7,5;7). В какой точке отрезка [−5;−2] функция $f(x)$ принимает наименьшее значение?
Решение
На отрезке [−5;−2] производная функции $y=f′(x)$ положительна, следовательно, $f(x)$ на этом отрезке возрастает и принимает наименьшее значение на левом конце отрезка (или, другими словами, при наименьшем значении x). В данном случае это $x=−5$.
Задача 17
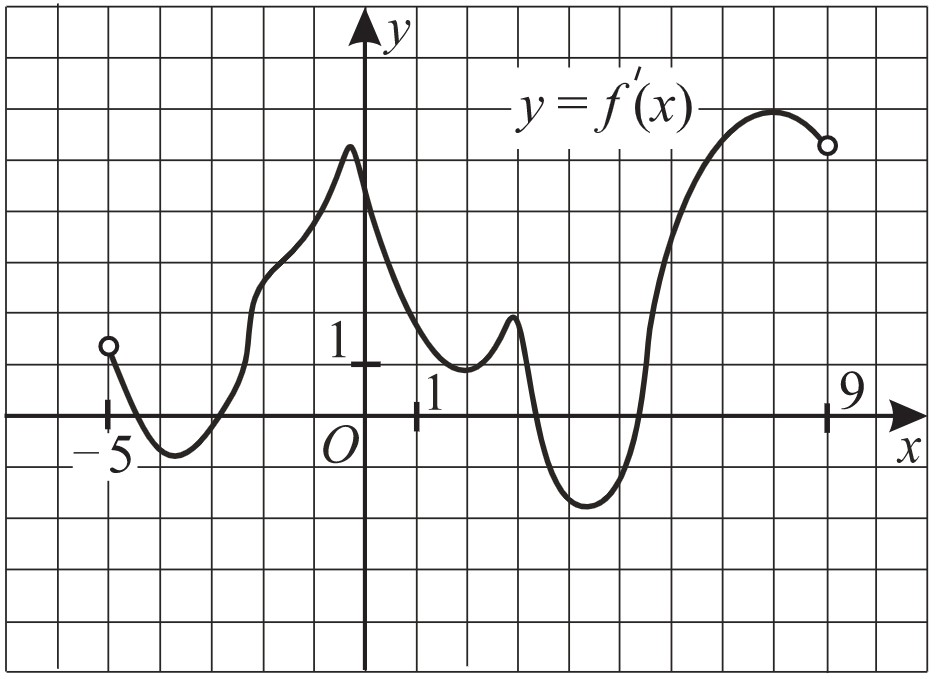
На рисунке изображён график производной функции $f(x)$, определённой на интервале (−5;9). Найдите промежутки убывания функции $f(x)$. В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение
$f(x)$ убывает, значит $f′(x)<0,$ точки $x_1=−4, x_2=−3$
$x_3=4, x_4=5$ - целые значения аргумента, удовлетворяющих условию
$−4+(−3)+4+5=2$
Задача 18
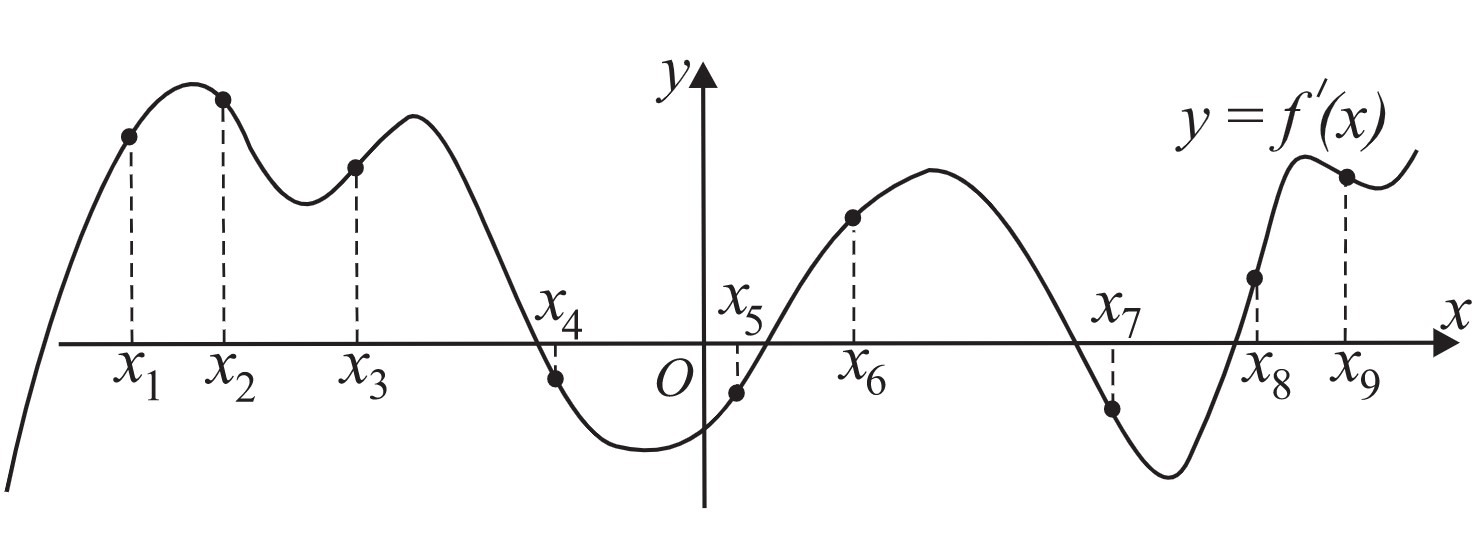
На рисунке изображён график $y=f′(x)$ производной функции $f(x)$ и девять точек на оси абсцисс: $x_1, x_2, x_3,…,x_9$. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?
Решение
Промежутком возрастания(где $f′(x)>0$) принадлежат точки $x_1;x_2;x_3;x_6;x_8;x_9$, значит 6 точек.
Задача 19
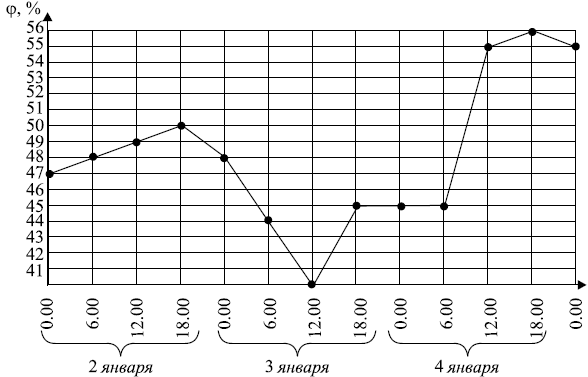
На рисунке точками показаны значения относительной влажности воздуха на складе дорогой мебели на протяжении трёх суток со 2 по 4 января 2016 года. Показатели влажности на этом складе заносятся в журнал каждые 6 часов, начиная с полуночи. По горизонтали указывается время, по вертикали относительная влажность в процентах. Для наглядности точки соединены линиями.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику влажности воздуха.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 2 января с 0:00 до 18:00 Б) 3 января с 0:00 до 12:00 В) с 18:00 3 января по 6:00 4 января Г) с 12:00 до полуночи 4 января | 1) влажность резко понижалась 2) влажность не изменялась 3) влажность равномерно повышалась 4) влажность была не менее 55% |
Под каждой буквой укажите соответствующий номер.
Решение
A) 2.01. с 0.00 до 18.00 - равномерно повышалась (3)
Б) 3.01. c 0.00 до 12.00 - резко повышалась (1)
B) c 18.00 3.01. по 6.00 4.01 - не изменялась (2)
Г) c 12.00 до 20.00 4.01 - была не менее 55% (4)
Задача 20
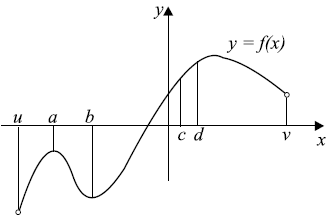
Точки $a, b, c$ и $d$ делят область определения $(u; v)$ функции $y = f(x)$, изображённой на рисунке, на пять промежутков. Установите соответствие между промежутками из левого столбца и характеристиками функции или её производной из правого столбца.
| ПРОМЕЖУТКИ | ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ЕЁ ПРОИЗВОДНОЙ |
| А) $(u; a)$ Б) $(a; b)$ В) $(b; c)$ Г) $(c; d)$ | 1) во всех точках промежутка значения функции отрицательны, а значения производной положительны 2) значения функции имеют разные знаки, а значения производной положительны во всех точках 3) во всех точках промежутка значения функции и значения производной отрицательны 4) во всех точках промежутка значения функции и значения производной положительны |
Под каждой буквой укажите соответствующий номер.
Решение
Для решения задачи давайте рассмотрим, что означает каждый из промежутков и характеристик функции или её производной:
А) (u; a)
На промежутке от $u$ до $a$ значения функции отрицательны, и производная положительна. Это означает, что функция убывает (значения функции отрицательны), а её производная положительна (функция возрастает).
Соответствие: 1.
Б) (a; b)
На промежутке от $a$ до $b$ значения функции изменяются с отрицательных на положительные, а производная остаётся положительной. Это предполагает, что функция возрастает, а производная положительна.
Соответствие: 3.
В) (b; c)
На промежутке от $b$ до $c$ значения функции и производной обе отрицательны, что предполагает, что функция убывает и её производная также отрицательна.
Соответствие: 2.
Г) (c; d)
На промежутке от $c$ до $d$ значения функции и производной положительны, что означает, что функция возрастает и её производная положительна.
Соответствие: 4.
Рекомендуемые курсы подготовки

- 👻 Вспомнишь алгебраические преобразования
- 👻 Отработаешь линейные, квадратные и дробно-рациональные уравнения
- 👻 Покоришь движение по воде
- 👻 И в целом крайне продуктивно проведешь время
на бесплатном курсе Турбо ЕГЭ

