Задание 18. Неравенства. Координатная прямая. ЕГЭ 2026 по математике (базовой)
Средний процент выполнения: 32.5%
Алгоритм решения задания 18:
- Определить вид неравенства и используемые в нём выражения.
- Привести неравенство к виду, удобному для анализа.
- Выделить точки, в которых выражение обращается в ноль или не определено.
- Разбить числовую прямую на промежутки по найденным точкам.
- Определить, на каких промежутках выполняется неравенство.
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
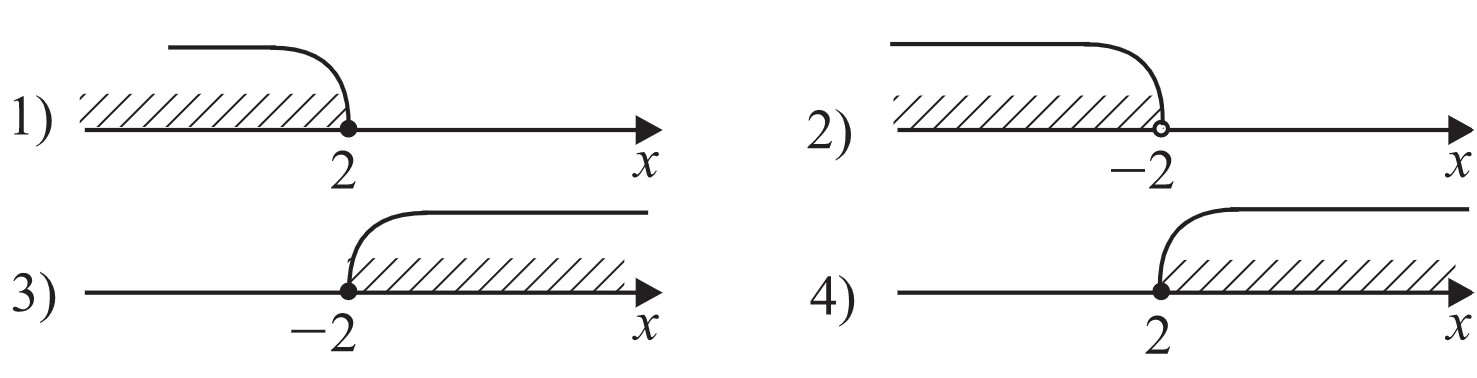
Решите неравенство $14+2(−x+7)⩽24$. На какой из координатных прямых (см. рис.) изображено множество его решений?
Решение
$14+2(−x+7)⩽24$
$14−2x+14⩽24$
$28−2x⩽24$
$−2x⩽−4$
$x⩾2$
Ответ: $[2;+∞)$ ( рисунок 4)
Задача 2
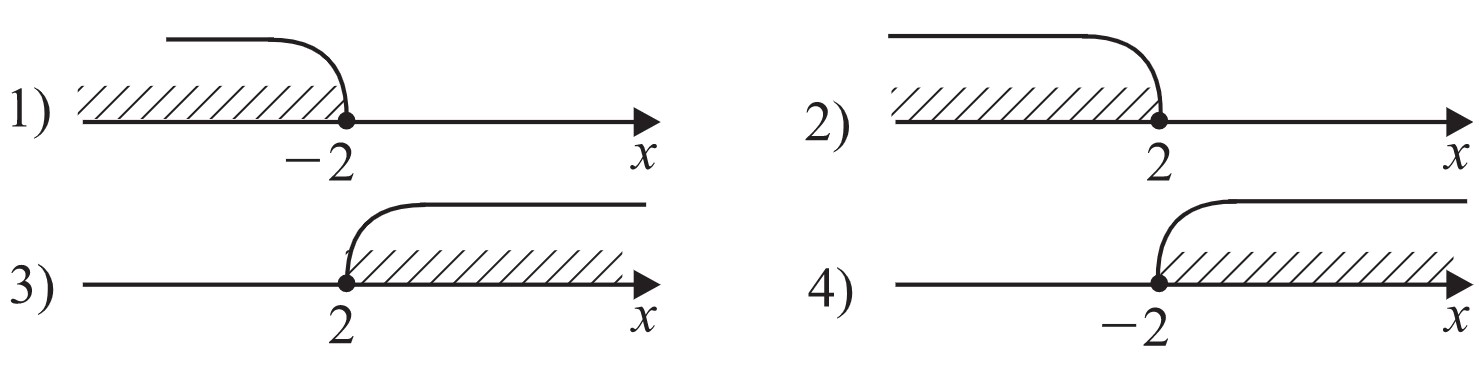
Решите неравенство $6+3(−2x+3)⩽3$. На какой координатной прямой (см. рис.) изображено множество его решений?
Решение
$6+3(−2x+3)⩽3$
$6−6x+9⩽3$
$15−6x⩽3$
$−6x⩽−12$
$x⩾2$
Ответ: $[2;+∞)$ ( рисунок 3)
Задача 3
Решите неравенство $8x−3(2x−1)⩽−2$
1) $[2,5;+∞)$
2) $(−∞;−2,5]$
3) $(−∞;2,5]$
4) $[−2,5;+∞)$
Решение
$8x−3(2x−1)⩽−2$
$8x−6x+3⩽−2$
$2x+3⩽−2$
$2x⩽−5$
$x⩽−2.5$
Ответ: $(−∞;−2.5]$ (вариант 2)
Задача 4
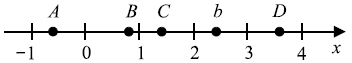
На прямой отмечены число b и точки A, B, C и D. Установите соответствие между указанными точками и числами в правом столбце, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A B C D | 1) $b -3$ 2) ${b^2}/{4}$ 3) ${2}/{b}$ 4) $6 - b$ |
Под каждой буквой укажите соответствующий номер.
Решение
1) $b -3=2,4-3=-0,6$ - точка А
2) ${b^2}/{4}={2,4^2}/{4}=1,44$ - точка С
3) ${2}/{b}=2/2.4=0.8$ - точка B
4) $6 - b=6-2.4=3.6$ - точка D
Задача 5
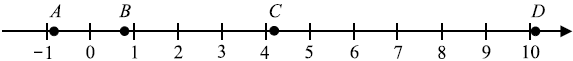
На координатной прямой отмечены точки $A, B, C$ и $D$, число $n$ равно $log_{2}9$. Установите соответствие между указанными точками из левого столбца и числами из правого столбца, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A B C D | 1) $n + 1$ 2) $n^2$ 3) $-{3}/{n}$ 4) $4 - n$ |
В под каждой буквой укажите соответствующий номер.
Решение
$n = \log_2 9 ≈3.17$
1) $n + 1 ≈4.17$
2) $n^2≈10.05$
3) $-{3}/{n} ≈ -0.95$
4) $4 - n ≈ 0.83$
На координатной прямой: A ≈ -0.95, B ≈ 0.83, C ≈ 4.17, D ≈ 10.05
A → 3, B → 4, C → 1, D → 2
Задача 6
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $log_5 x > 1$ Б) $log_5 x < 1$ В) $log_5 x > -1$ Г) $log_5 x < -1$ | 1) $(0; 5)$ 2) $(0.2;+∞)$ 3) $(5;+∞)$ 4) $(0; 0.2)$ |
Под каждой буквой укажите соответствующий номер.
Решение
A) $log_5x > 1$ $x > 5$ $x∈(5; +∞)$ (3)
Б) $log_5x < 1$ $0 < x < 5$ $x∈(0;5)$ (1)
B) $log_5x > -1$ $x > {1}/{5}$ $x∈({1}/{5};+∞)$ (2)
Г) $log_5x < -1$ $0 < x < {1}/{5}$ $x∈(0;{1}/{5})$ (4)
Задача 7
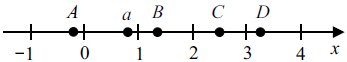
На прямой отмечены число a и точки A, B, C и D.
Установите соответствие между указанными точками и числами в правом столбце, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A B C D | 1) ${2}/{a}$ 2) $4 - a$ 3) $2a^2$ 4) $a - 1$ |
Под каждой буквой укажите соответствующий номер.
Решение
Предположим, что мы имеем число:
- Пусть a = 0.8:
- Точка A: A = a - 1 = 0.8 - 1 = -0.2
- Точка B: B = 2a² = 2 * (0.8²) = 2 * 0.64 = 1.28
- Точка C: C = 2/a = 2/0.8 = 2.5
- Точка D: D = 4 - a = 4 - 0.8 = 3.2
Заключение:
На основании вышеизложенного, установленные соответствия между точками и числами будут следующими:
- A - 4
- B - 3
- C - 1
- D - 2
Задача 8
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $5^x ≥ 5$ Б) $0.2^x ≥ 5 $ В) $0.2^x ≤ 5$ Г) $5^x ≤ 5$ | 1) $[1;+∞)$ 2) $(-∞;-1]$ 3) $(-∞; 1]$ 4) $[-1;+∞)$ |
Под каждой буквой укажите соответствующий номер.
Решение
А) $5^x ≥ 5$ → $x ≥ 1$ → 1
Б) $0.2^x ≥ 5$ → $0.2^x ≥ 0.2^{-1}$ → $x ≤ -1$ → 2
В) $0.2^x ≤ 5$ → $0.2^x ≤ 0.2^{-1}$ → $x ≥ -1$ → 4
Г) $5^x ≤ 5$ → $x ≤ 1$ → 3
Ответ: 1243
Задача 9
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $3^x ≥ 3$ Б) $0.3^x≥ {10}/{3}$ В) $0.3^x ≤ {10}/{3}$ Г) $3^x ≤ 3$ | 1) $(-∞; 1]$ 2) $[1;+∞)$ 3) $[-1;+∞)$ 4) $(-∞;-1]$ |
Под каждой буквой укажите соответствующий номер.
Решение
Приведём \(3\) к степени \(3^1\):
\(3^x ≥ 3^1\)
Так как основание \(3 > 1\), знак неравенства сохраняется:
\(x ≥ 1\)
Решение: \([1; +∞)\)
Преобразуем: \(0.3^x = (1 / 3)^x\). Подставим это в неравенство:
$$ (1 / 3)^x ≥ 10 / 3$$
Возьмем логарифм по основанию \(3\) и учтем, что основание дробное (меньше 1), поэтому знак неравенства меняется:
$$x ≤ -1$$
Решение: \((-∞; -1]\)
Преобразуем аналогично предыдущему случаю:
$$ (1 / 3)^x ≤ 10 / 3$$
Берем логарифм и меняем знак на противоположный:
$$x ≥ -1$$
Решение: \([-1; +∞)\)
Представим \(3\) как \(3^1\):
$$3^x ≤ 3^1$$
Так как основание \(3 > 1\), знак сохраняется:
$$x ≤ 1$$
Решение: \((-∞; 1]\)
Задача 10
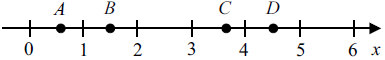
На координатной прямой отмечены точки $A, B, C$ и $D$, число $m$ равно $√5$. Установите соответствие между указанными точками из левого столбца и числами из правого столбца, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A B C D | 1) ${m^3}/{3}$ 2) ${m}/{4}$ 3) $√m$ 4) $2m$ |
В под каждой буквой укажите соответствующий номер.
Решение
Шаг 1: Подставляем значение m в каждое выражение и вычисляем:
1) Выражение: ${m^3}/{3}$
Подставляем m:
${(√5)^3}/{3} = {5√5}/{3} ≈ 9.81/3 ≈ 3.27$
2) Выражение: ${m}/{4}$
Подставляем m:
${√5}/{4} ≈ 2.236/4 ≈ 0.559$
3) Выражение: $√m$
Подставляем m:
$√{√5} = 5^{1/4} ≈ 1.495$
4) Выражение: $2m$
Подставляем m:
$2 * √5 ≈ 2 * 2.236 ≈ 4.472$
Шаг 2: Сравниваем значения:
- A: ${m}/{4} ≈ 0.559$
- B: $√m ≈ 1.495$
- C: ${m^3}/{3} ≈ 3.27$
- D: $2m ≈ 4.472$
Ответ:
A - 2
B - 3
C - 1
D - 4
Задача 11
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $x^2 - 3x - 4 ≤ 0$ Б) $x^2 - 3x + 2 ≥ 0$ В) $x^2 + 3x - 4 ≥ 0$ Г) $x^2 + 3x + 2 ≤ 0$ | 1) $(-∞;-4] ∪ [1;+∞)$ 2) $[-1; 4]$ 3) $(-∞; 1] ∪[2;+∞)$ 4) $[-2;-1]$ |
Под каждой буквой укажите соответствующий номер.
Решение
А) $x^2 - 3x - 4 ≤ 0$ → Корни: $x=-1$, $x=4$ → Решение: $[-1;4]$ → 2
Б) $x^2 - 3x + 2 ≥ 0$ → Корни: $x=1$, $x=2$ → Решение: $(-∞;1] ∪ [2;+∞)$ → 3
В) $x^2 + 3x - 4 ≥ 0$ → Корни: $x=-4$, $x=1$ → Решение: $(-∞;-4] ∪ [1;+∞)$ → 1
Г) $x^2 + 3x + 2 ≤ 0$ → Корни: $x=-2$, $x=-1$ → Решение: $[-2;-1]$ → 4
Ответ: 2314
Задача 12
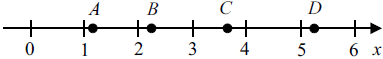
На числовой прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A B C D | 1) $({5}/{18})^{-1}$ 2) ${21}/{4}$ 3) $log_{3}4$ 4) $√{4.9}$ |
В под каждой буквой укажите соответствующий номер.
Решение
2) ${21}/{4}=5.25$ - точка D.
4) $√{4.9}$ находится в промежутке от $√{4}$ до $√{9}$, то есть между 2 и 3 - точка B.
3) $log_{3}4$ - точка А.
Задача 13
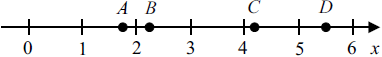
На числовой прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A B C D | 1) $({5}/{21})^{-1}$ 2) ${11}/{2}$ 3) $log_{2}5$ 4) $√{3.2}$ |
В под каждой буквой укажите соответствующий номер.
Решение
1) $({5}/{21})^{-1} = {21}/{5} = 4.2$
2) ${11}/{2} = 5.5$
3) $\log_{2}5 ≈ 2.32$
4) $√{3.2} ≈ 1.79$
На числовой прямой: A ≈ 1.79, B ≈ 2.32, C ≈ 4.2, D ≈ 5.5
A → 4, B → 3, C → 1, D → 2
Задача 14
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $x^2 - 3x - 4 ≥ 0$ Б) $x^2 - 3x + 2 ≤ 0 $ В) $x^2 + 3x - 4 ≤ 0 $ Г) $x^2 + 3x + 2 ≥ 0$ | 1) $x ≤ -1$ или $x ≥ 4$ 2) $1 ≤ x ≤ 2$ 3) $x ≤ -2$ или $x ≥ -1$ 4) $-4 ≤ x ≤ 1$ |
Под каждой буквой укажите соответствующий номер.
Решение
- A) $x^2 - 3x - 4 ≥ 0$:
- $(-\infty, -1)$: положительно.
- $(-1, 4)$: отрицательно.
- Б) $x^2 - 3x + 2 ≤ 0$:
- $(-\infty, 1)$: положительно.
- В) $x^2 + 3x - 4 ≤ 0$:
- $(-\infty, -4)$: положительно.
- Г) $x^2 + 3x + 2 ≥ 0$:
- $(-\infty, -2)$: положительно.
Находим корни уравнения:
$x^2 - 3x - 4 = (x - 4)(x + 1) = 0$, следовательно, корни: $x_1 = 4$, $x_2 = -1$.
Проверяем знаки на интервалах:
Решение: $x ≤ -1$ или $x ≥ 4$. Это соответствует решению (1).
Находим корни уравнения:
$x^2 - 3x + 2 = (x - 1)(x - 2) = 0$, следовательно, корни: $x_1 = 1$, $x_2 = 2$.
Проверяем знаки на интервалах:
Решение: $1 ≤ x ≤ 2$. Это соответствует решению (2).
Находим корни уравнения:
$x^2 + 3x - 4 = (x + 4)(x - 1) = 0$, следовательно, корни: $x_1 = -4$, $x_2 = 1$.
Проверяем знаки на интервалах:
Решение: $-4 ≤ x ≤ 1$. Это соответствует решению (4).
Находим корни уравнения:
$x^2 + 3x + 2 = (x + 1)(x + 2) = 0$, следовательно, корни: $x_1 = -1$, $x_2 = -2$.
Проверяем знаки на интервалах:
Решение: $ x ≤ −2$ или $ x ≥ −1$. Это соответствует решению(3).
Итоговое соответствие:
- A - 1
- Б - 2
- В - 4
- Г - 3
Задача 15
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $x^2 - 5x + 4 ≤ 0$ Б) $x^2 - 5x - 6 ≥ 0$ В) $x^2 + 5x + 4 ≥ 0$ Г) $x^2 + 5x + 6 ≤ 0$ | 1) $(-∞;-1] ∪ [6;+∞)$ 2) $(-∞; -4] ∪[-1;+∞)$ 3) $[1; 4]$ 4) $[-3;-2]$ |
Под каждой буквой укажите соответствующий номер.
Решение
А) $x^2 - 5x + 4 ≤ 0$ → Корни: $x=1$, $x=4$ → Решение: $[1;4]$ → 3
Б) $x^2 - 5x - 6 ≥ 0$ → Корни: $x=-1$, $x=6$ → Решение: $(-∞;-1] ∪ [6;+∞)$ → 1
В) $x^2 + 5x + 4 ≥ 0$ → Корни: $x=-4$, $x=-1$ → Решение: $(-∞;-4] ∪ [-1;+∞)$ → 2
Г) $x^2 + 5x + 6 ≤ 0$ → Корни: $x=-3$, $x=-2$ → Решение: $[-3;-2]$ → 4
Ответ: 3124
Задача 16
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $5^x≥ 5 $ Б)$({1}/{5})^x≤5$ В)$({1}/{5})^x≥5$ Г) $5^x≤5$ | 1) 2)  3)  4)  |
Под каждой буквой укажите соответствующий номер.
Решение
Решим каждое неравенство:
__________________________________________________________________________
A) $5^x ≥ 5$
$5^x ≥ 5$
$5^x ≥ 5^1->$поскольку основание степени больше единицы, показатели соотносятся аналогичным знаком:
$x ≥ 1$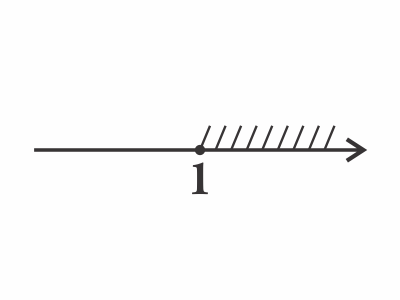 Тогда $A-2$.
Тогда $A-2$.
__________________________________________________________________________
Б) $({1}/{5})^x ≤ 5$
$({1}/{5})^x ≤ ({1}/{5})^{-1} ->$ поскольку основание степени меньше единицы, показатели соотносятся обратным знаком:
$x ≥ -1$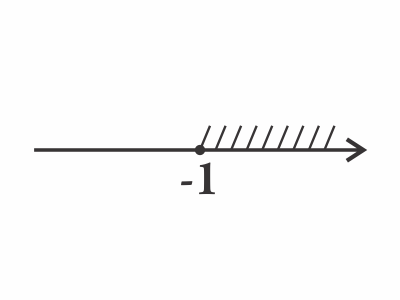 Тогда $Б-3$.
Тогда $Б-3$.
__________________________________________________________________________
B) $({1}/{5})^x ≥ 5$
$({1}/{5})^x ≥ ({1}/{5})^{-1}->$ поскольку основание меньше единицы, показатели соотносятся обратным знаком:
$x ≤ -1$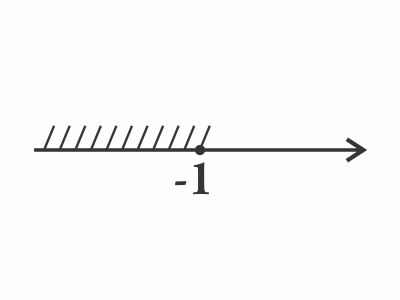 Тогда $В-1$.
Тогда $В-1$.
__________________________________________________________________________
Г) $5^x ≤ 5$
$5^x ≤ 5^1 ->$ поскольку основание больше единицы, показатели соотносятся аналогичным знаком:
$x ≤ 1$ 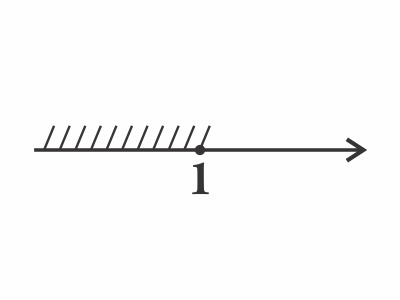 Тогда $Г-4$
Тогда $Г-4$
Задача 17
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $log_{13} x > -1$ Б) $log_{13} x < 1$ В) $log_{13} x < -1$ Г) $log_{13} x > 1$ | 1) $x > 13$ 2) $0 < x < {1}/{13}$ 3) $x > {1}/{13}$ 4) $0 < x < 13$ |
Под каждой буквой укажите соответствующий номер.
Решение
А) $\log_{13} x > -1$ → $x > 13^{-1}$ → $x > \frac{1}{13}$ → 3
Б) $\log_{13} x < 1$ → $x < 13^1$ → $0 < x < 13$ → 4
В) $\log_{13} x < -1$ → $x < 13^{-1}$ → $0 < x < \frac{1}{13}$ → 2
Г) $\log_{13} x > 1$ → $x > 13^1$ → $x > 13$ → 1
Ответ: 3421
Задача 18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $log_7x<1$ Б) $log_7 x < -1 $ В) $log_7 x > 1$ Г) $log_7 x > -1 $ | 1)$({1}/{7};+∞)$ 2)$(7;+∞)$ 3)$(0;7)$ 4)$(0;{1}/{7})$ |
Под каждой буквой укажите соответствующий номер.
Решение
A) $log_7x < 1$ $0 < x < 7$ $x∈(0; 7)$(3)
Б) $log_7x < -1$ $0 < x < {1}/{7}$ $x∈(0; {1}/{7})$ (4)
B) $log_7x > 1$ $x > 7$ $x∈(7; +∞)$ (2)
Г) $log_7x > -1$ $x > {1}/{7}$ $x∈({1}/{7}; +∞)$ (1)
Задача 19
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) $0.4^x ≥ {5}/{2}$ Б) $4^x ≤ 4$ В) $0.4^x ≤ {5}/{2}$ Г) $4^x ≥ 4$ | 1) 2)  3)  4)  |
Под каждой буквой укажите соответствующий номер.
Решение
A) $0,4^x ≥ {5}/{2}$ $0,4^x ≥ 0,4^{-1}; x ≤ -1$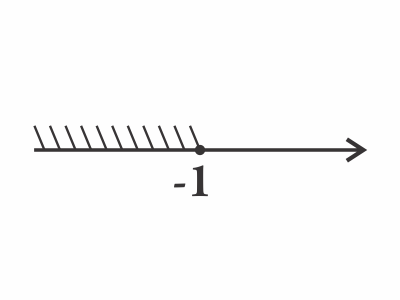 (1)
(1)
Б) $4^x ≤ 4$ $x ≤ 1$ 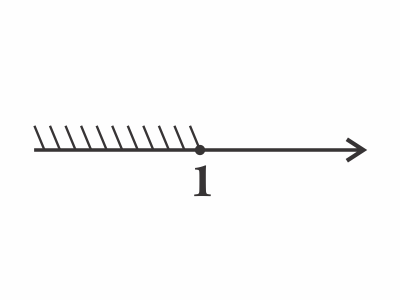 (4)
(4)
В) $0,4^x ≤ {5}/{2}$ $0,4^x ≤ 0,4^{-1}; x ≥ -1$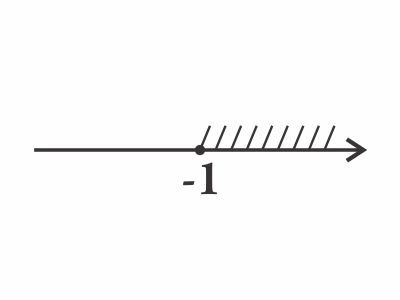 (3)
(3)
Г) $4^x ≥ 4$ $x ≥ 1$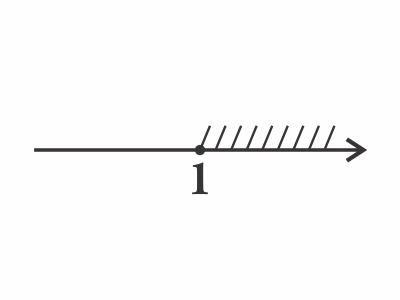 (2)
(2)
Задача 20
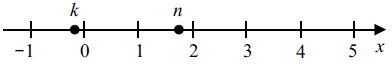
На прямой отмечены числа $n$ и $k$.
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами из левого столбца и отрезками из правого столбца.
| ЧИСЛА | ОТРЕЗКИ |
| А) ${1}/{n} + k$ Б) $n + k$ В) $nk$ Г) $n^2 - k^2$ | 1) $[-1;0]$ 2) $[0; 1]$ 3) $[1; 2]$ 4) $[2; 4]$ |
Под каждой буквой укажите соответствующий номер.
Решение
$n$ примерно $1,7$, $k$ примерно $-0,2$.
А) ${1}/{n} + k=1/1,7+(-0,2)$ - промежуток под цифрой 2.
Б) $n + k = 1,7+(-0,2)$- промежуток под цифрой 3
В) $nk=1,7*(-0,2)$- промежуток под цифрой 1
Г) $n^2 - k^2=(1,7)^2-(-0,2)^2$- промежуток под цифрой 4
Рекомендуемые курсы подготовки

- 👻 Вспомнишь алгебраические преобразования
- 👻 Отработаешь линейные, квадратные и дробно-рациональные уравнения
- 👻 Покоришь движение по воде
- 👻 И в целом крайне продуктивно проведешь время
на бесплатном курсе Турбо ЕГЭ

