Теория графов для ЕГЭ по информатике: полный гид от основ до решения задач

Зачем нужна теория графов на ЕГЭ

В КИМах 2024-2025 годов задачи по графам встречаются в заданиях №1 (подсчет путей). Даже один правильно решённый граф может принести тебе лёгкий и уверенный балл на ЕГЭ!

А теперь о приятном: теория графов используется повсюду в реальной жизни. Когда Яндекс.Карты строят маршрут от дома до школы — это алгоритм поиска кратчайшего пути в графе. Когда ты листаешь ВКонтакте рекомендации друзей — это анализ социального графа. Даже интернет — это огромный граф, где сайты — вершины, а ссылки между ними — ребра.

💡 Совет: Теория графов кажется абстрактной, но стоит провести параллель с картами и дорогами — и всё встаёт на свои места. Дальше я покажу, как превратить любую задачу в простую схему.

Что такое граф: основные понятия простым языком

Граф — это математическая структура, которая показывает связи между объектами. Думай о нём как о карте: есть города (их называют вершинами) и дороги между ними (это ребра или дуги).

Представь пять городов: Москва, Санкт-Петербург, Казань, Нижний Новгород и Екатеринбург. Между некоторыми из них есть прямые авиарейсы. Если нарисовать эту ситуацию, получится граф: каждый город — точка (вершина), каждый авиарейс — линия между точками (ребро).

Виды графов

Ориентированные и неориентированные графы

Если дорога между городами работает в обе стороны — это неориентированный граф. Если есть улица с односторонним движением — ориентированный граф (на схеме рёбра помечают стрелками).

Пример из жизни: ВКонтакте дружба взаимная (неориентированный граф), а в Instagram (деятельность компании meta признана экстремистской на территории РФ) можно подписаться на человека, который не подписан на тебя (ориентированный граф).

Взвешенные и невзвешенные графы

Если важно не только наличие дороги, но и её длина, время в пути или стоимость проезда — это взвешенный граф. Числа на рёбрах называют весами. Если веса нет — граф невзвешенный.

На ЕГЭ чаще всего встречаются взвешенные графы, где веса — это расстояния или время.

Связные и несвязные графы

Представь архипелаг: несколько островов с мостами между ними. Если из любого острова можно добраться до любого другого по мостам — это связный граф. Если есть изолированные острова — несвязный граф.

Ключевые термины

Степень вершины — количество ребер, которые из нее выходят. Если к вершине А подходит 3 ребра, ее степень равна 3. Это часто спрашивают на ЕГЭ!

Путь — последовательность вершин, где каждая следующая соединена ребром с предыдущей, и вершины не повторяются. Например: A → B → C.

Маршрут — то же самое, но вершины могут повторяться. Можно пройти A → B → A → C.

Цикл — путь, который начинается и заканчивается в одной вершине. Представь, что вышел из дома, погулял по району и вернулся домой.

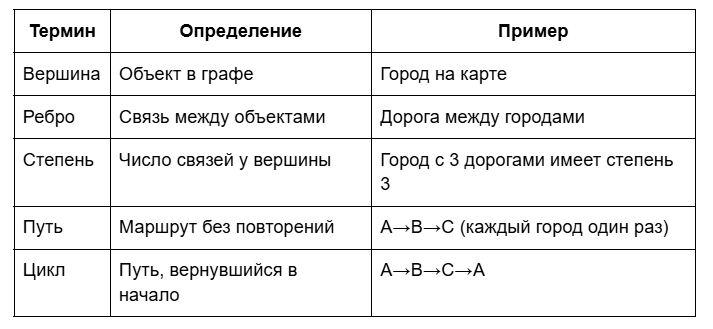
⚠️ Частая ошибка: Путать путь и маршрут. Запомни: в пути нельзя возвращаться в уже посещенные вершины!

Способы представления графов

На ЕГЭ граф может быть представлен тремя способами. Умение переходить от одной формы к другой — ключевой навык.

Графическое представление

Самый наглядный способ — схема с точками и линиями. Вершины обозначают буквами или цифрами, рёбра рисуют линиями. Если граф взвешенный, веса пишут рядом с рёбрами.

Как читать схему:

• Найди все вершины (точки)
• Посмотри, какие из них соединены
• Обрати внимание на веса (числа у рёбер)
• Проверь направление стрелок (если есть)

Матрица смежности

Матрица смежности — это таблица, где строки и столбцы соответствуют вершинам графа. В ячейке на пересечении строки А и столбца Б стоит:

• 1 (или вес ребра), если между А и Б есть связь
• 0, если связи нет

Рассмотрим пример. Есть граф с четырьмя вершинами: A, B, C, D. Рёбра: A-B (вес 5), A-C (вес 3), B-C (вес 2), C-D (вес 4).

Матрица смежности:

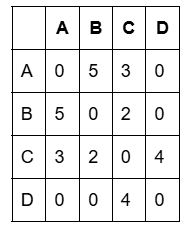
Как заполнять пошагово:

1. Нарисуй таблицу N×N (где N — число вершин)
2. Подпиши строки и столбцы одинаковыми буквами
3. Для каждой пары вершин проверь, есть ли ребро
4. Впиши вес ребра (или 1) в соответствующую ячейку
5. Если граф неориентированный, заполни симметрично

Как определить степень вершины: просуммируй все ненулевые значения в строке (или столбце) этой вершины. У вершины C степень = 3 (связана с A, B и D).

✅ Лайфхак: В неориентированном графе матрица симметрична относительно главной диагонали. Используй это для проверки!

Список рёбер

Простое перечисление всех связей: (A, B, 5), (A, C, 3), (B, C, 2), (C, D, 4). Формат: (откуда, куда, вес).

Таблица с весами

Иногда на ЕГЭ дают таблицу, где в строках указаны начальные вершины, в столбцах — конечные, а в ячейках — расстояния. Это тоже матрица смежности, просто без нулей для наглядности.

💡 Совет: Учись быстро строить матрицу по схеме и наоборот. На экзамене это сэкономит драгоценное время!

Практическое задание: Нарисуй граф с вершинами 1, 2, 3, 4, 5 и рёбрами: 1-2 (вес 7), 1-3 (вес 4), 2-4 (вес 3), 3-4 (вес 2), 4-5 (вес 5). Составь для него матрицу смежности. Проверь себя: степень вершины 4 должна быть равна 3.

Типовые задачи ЕГЭ по теории графов

Подсчёт количества путей (задание 1, 3)

Это классика ЕГЭ. Задача звучит так: "Сколько существует различных путей из вершины А в вершину Е?" Или: "Сколько путей длиной не более N рёбер?"

Алгоритм решения:

1. Нарисуй граф или используй данную схему
2. Выпиши все возможные маршруты пошагово
3. Исключи те, где вершины повторяются (если требуется путь)
4. Подсчитай количество

Разбор задачи №1:

Условие: На рисунке представлена схема дорог между пятью населенными пунктами A, B, C, D, E. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из A в E?

Схема: A → B, A → C, B → D, C → B, C → D, D → E

Решение:

Шаг 1: Строим граф мысленно или на бумаге.

Шаг 2: Идем из A. Из A можем попасть в B или C.

Шаг 3: Если выбрали A → B, то из B идем в D (B → D), далее D → E. Путь 1: A → B → D → E

Шаг 4: Если выбрали A → C, то из C можем попасть в B или D.

• A → C → B → D → E (Путь 2)
• A → C → D → E (Путь 3)

Шаг 5: Итого 3 пути.

Ответ: 3

⚠️ Частая ошибка: Забывать, что в пути вершины не повторяются. Если в условии написано "путь", нельзя проходить через одну точку дважды!

Разбор задачи №2:

Условие: Между населёнными пунктами A, B, C, D, E построены дороги (неориентированный граф). Сколько путей ведет из A в E, которые проходят через B?

Ребра: A-B, A-C, B-C, B-D, C-D, D-E, C-E

Решение:

Если путь должен проходить через B, разобьем задачу на две части: сколько путей из A в B, и сколько из B в E.

Из A в B:

• A → B (Путь 1)
• A → C → B (Путь 2)

Из B в E (не возвращаясь в A):

• B → D → E (Путь 1)
• B → C → E (Путь 2)
• B → C → D → E (Путь 3)
• B → D → C → E (но это значит, что мы уже были в C, если пришли из A через C — проверяем каждый вариант отдельно)

Комбинируем:

• Если шли A → B, то можем: B → D → E, B → C → E, B → C → D → E (3 варианта)
• Если шли A → C → B, то можем: B → D → E, B → D → C → E (2 варианта, так как в C уже были)

Итого: 3 + 2 = 5 путей

Ответ: 5

✅ Лайфхак: Для сложных графов используй таблицу: в первом столбце пиши "количество путей до вершины X", заполняй пошагово от стартовой вершины.

Поиск кратчайшего пути

Когда нужно найти минимальное расстояние между вершинами — это задача на кратчайший путь. Самый популярный алгоритм — алгоритм Дейкстры.

Алгоритм Дейкстры простыми словами:

Представь, что ты стоишь в точке А и хочешь добраться до точки F максимально быстро. Ты не знаешь всю карту сразу, но видишь ближайшие точки.

1. Пометь стартовую вершину расстоянием 0, остальные — бесконечностью (∞)
2. Выбери непосещенную вершину с минимальным расстоянием
3. Для всех её соседей пересчитай расстояние: если через текущую вершину путь короче — обнови
4. Пометь текущую вершину как посещенную
5. Повтори шаги 2-4, пока не дойдёшь до целевой вершины

Разбор задачи:

Условие: Найди кратчайший путь из A в F.

Граф: A-B (7), A-C (9), B-C (10), B-D (15), C-D (11), C-E (2), D-F (6), E-F (9)

Решение в таблице:

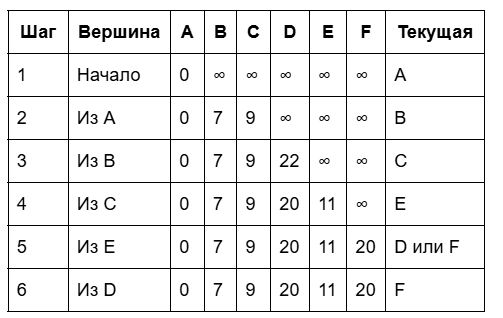
Пошагово:

1. Начинаем в A (расстояние 0)
2. Из A можем попасть в B (7) и C (9). Минимум — B.
3. Из B проверяем соседей: C (через B = 7+10=17 > 9, не обновляем), D (7+15=22).
4. Следующая ближайшая — C (9). Из C: D (9+11=20 < 22, обновляем), E (9+2=11).
5. Следующая — E (11). Из E: F (11+9=20).
6. Следующая — D (20) или F (20). Из D до F: 20+6=26 > 20. Кратчайший путь до F = 20.

Ответ: 20 (путь: A → C → E → F)

💡 Совет: На экзамене оформляй решение таблицей — это компактно, понятно проверяющему и помогает не запутаться.

Практическое задание: Найди кратчайший путь от A до E в графе: A-B (3), A-C (5), B-D (4), C-D (2), C-E (6), D-E (3). Ответ: 10 (A → C → D → E).

Алгоритмы для работы с графами

Для полноты картины разберём три ключевых алгоритма, которые полезны для понимания, но на базовом уровне ЕГЭ встречаются редко.

Обход в глубину (DFS)

Представь, что ты исследуешь лабиринт. Идёшь по одному коридору до упора, затем возвращаешься и пробуешь другой. DFS работает так же: углубляется в один путь максимально, затем откатывается.

Когда применять: проверка связности графа, поиск циклов, топологическая сортировка.

Обход в ширину (BFS)

Теперь представь, что обследуешь территорию кругами: сначала всё в радиусе 1 метр, потом 2 метра, потом 3. BFS идёт по уровням: сначала все соседи стартовой вершины, потом соседи соседей.

Когда применять: поиск кратчайшего пути в невзвешенном графе, определение минимального числа ребер между вершинами.

Алгоритм Флойда-Уоршелла

Это способ найти кратчайшие пути между всеми парами вершин сразу. Алгоритм проверяет: можно ли сократить расстояние между любыми двумя точками, пройдя через третью?

Когда применять: когда нужно найти кратчайшие пути между всеми вершинами, а не от одной конкретной.

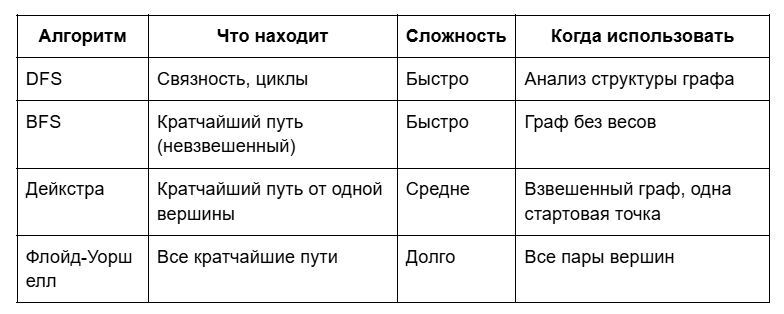
На ЕГЭ чаще всего достаточно Дейкстры или даже простого перебора для маленьких графов!

Связь теории графов с программированием

Иногда нужно реализовать алгоритм на графах в коде. Покажу базовые конструкции на Python.

Представление графа словарём (список смежности):

graph = {

    'A': {'B': 5, 'C': 3},

    'B': {'A': 5, 'C': 2, 'D': 4},

    'C': {'A': 3, 'B': 2, 'E': 6},

    'D': {'B': 4, 'E': 1},

    'E': {'C': 6, 'D': 1}}

Здесь graph['A'] возвращает словарь соседей вершины A с весами рёбер.

Простой поиск кратчайшего пути (Дейкстра):

import heapq

def dijkstra(graph, start, end):

  distances = {vertex: float('infinity') for vertex in graph}

  distances[start] = 0

  priority_queue = [(0, start)]

while priority_queue:

    current_distance, current_vertex = heapq.heappop(priority_queue)

    if current_vertex == end:

      return current_distance

    for neighbor, weight in graph[current_vertex].items():

      distance = current_distance + weight

      if distance < distances[neighbor]:

        distances[neighbor] = distance

        heapq.heappush(priority_queue, (distance, neighbor))

      return distances[end]

print(dijkstra(graph, 'A', 'E')) # Выведет кратчайшее расстояние

Чек-лист подготовки и типичные ошибки

Что нужно знать наизусть:

• Определения: граф, вершина, ребро, степень, путь, цикл
• Виды графов: ориентированный/неориентированный, взвешенный/невзвешенный
• Как читать матрицу смежности
• Алгоритм Дейкстры (общая логика)

Топ-5 ошибок на экзамене:

1. Путать путь и маршрут — в пути нельзя повторять вершины! Всегда проверяй условие.
2. Не учитывать направление рёбер — если граф ориентированный, из A в B можно, а обратно нет.
3. Забывать про веса — кратчайший путь не всегда тот, где меньше рёбер. Считай сумму весов!
4. Терять варианты при переборе — делай систематично, лучше с таблицей или деревом вариантов.
5. Неправильно заполнять матрицу — помни, что в неориентированном графе матрица симметрична.

Чек-лист перед экзаменом:

• ✅ Решил 10+ задач на подсчет путей
• ✅ Решил 10+ задач на кратчайший путь
• ✅ Умею быстро рисовать граф по матрице и наоборот
• ✅ Знаю алгоритм Дейкстры наизусть
• ✅ Потренировался на вариантах ФИПИ

Заключение

Теория графов — это не монстр, а твой друг на экзамене. Давай закрепим главное:

1. Граф — вершины и рёбра. Думай о картах и дорогах.
2. Матрица смежности — твой ключ к быстрому решению. Научись с ней работать.
3. Подсчёт путей — систематический перебор или таблица по шагам.
4. Кратчайший путь — алгоритм Дейкстры, оформляй таблицей.
5. Практика решает всё — чем больше задач, тем увереннее чувствуешь себя.

На подготовку к теории графов нужно 7-10 дней активной практики. Начни с простых задач, постепенно усложняй. Разбирай каждую ошибку — и через неделю ты будешь щёлкать эти задания как орешки.

Помни: на ЕГЭ по информатике каждый балл на счету. Теория графов может принести 1 первичный балл за несколько минут работы. Это отличная инвестиция времени!

Твой план на ближайшие дни:

• День 1-2: Изучи теорию, нарисуй 10 графов, составь для них матрицы
• День 3-4: Реши 15 задач на подсчет путей из банка ФИПИ
• День 5-6: Реши 10 задач на кратчайший путь, освой Дейкстру
• День 7: Пройди полноценный вариант, засекай время

Ты справишься! Теория графов станет твоим козырем на экзамене. Открывай банк заданий ФИПИ прямо сейчас и начинай практиковаться. Удачи на ЕГЭ! 🚀

Список использованных источников

1. Федеральный институт педагогических измерений (ФИПИ) — Открытый банк заданий ЕГЭ по информатике
2. Поляков К.Ю. "Информатика. Углублённый уровень" — учебник для 10-11 классов
3. Босова Л.Л., Босова А.Ю. "Информатика. Базовый уровень" — учебное пособие
4. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. "Алгоритмы: построение и анализ" — классический учебник по алгоритмам
5. Методические материалы для председателей и членов региональных предметных комиссий по проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ 2024 года (ФИПИ)