Задание 18. Задача с параметром. ЕГЭ 2026 по математике профильного уровня
Средний процент выполнения: 2%
Ответом к заданию 18 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Алгоритм решения задания 18:
Внимательно прочитать условие и определить, что требуется найти: решения уравнения, неравенства, системы или условия на параметр.
Выписать все выражения в явном виде и зафиксировать параметры, если они присутствуют.
Определить область допустимых значений переменных и параметров.
Выполнить тождественные преобразования, приводя выражения к более удобному виду.
Выбрать метод решения (алгебраический, графический, анализ функций) в соответствии с видом задачи.
Решить уравнение, неравенство или систему с учётом параметра, последовательно анализируя возможные случаи.
Проверить равносильность выполненных преобразований и исключить посторонние решения.
Проанализировать полученные решения с учётом области допустимых значений и условий задачи.
Сформулировать ответ в виде, соответствующем требованию задания (множество решений или условия на параметр).
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Найдите все значения параметра $a$, при каждом из которых уравнение ${x-4a} / {x+4}+{x-1} / {x-a}=1$ имеет единственный корень.
Решение
Преобразуем данное уравнение.
${(x - 4a)(x - a) + (x + 4)(x - 1) - (x + 4)(x - a)}/{(x + 4)(x - a)} = 0$,
${x^2 - ax - 4ax + 4a^2 + x^2 + 3x - 4 - x^2 + ax - 4x + 4a}/{(x + 4)(x - a)} = 0$,
${x^2 - x(4a + 1) + 4a^2 + 4a - 4}/{(x + 4)(x - a)} = 0$,
$\{\table\x^2 - x(4a + 1) + 4a^2 + 4a - 4 = 0; \(x + 4)(x - a) ≠ 0;$.
Решим уравнение $x^2 - x(4a + 1) + 4a^2 + 4a - 4 = 0$.
$x = {(4a + 1) ±√{-8a + 17}}/{2}$
1. При $D < 0$ уравнение корней не имеет.
2. При $D = 0, -8a + 17 = 0, a = {17}/{8}$. Уравнение имеет единственный корень $x = {4a + 1}/{2}$ при $a = {17}/{8}. x = {4 · {17}/{8} + 1}/{2} = 4.75$.
Выполнено условие $x ≠ -4, x ≠ a$.
Значит, $a = {17}/{8} = 2.125$ удовлетворяет условию задачи.
3. При $D > 0$ уравнение имеет два корня.
$x = {(4a + 1) ±√{17 - 8a}/{2}$.
Проверим при каких значениях $a$ значения $x = -4$ и $x = a$ являются корнями уравнения $x^2 - x(4a + 1) + 4a^2 + 4a - 4 = 0$.
При $x = -4$ должно выполняться равенство $16 + 4(4a + 1) + 4a^2 + 4a - 4 = 0, a^2 + 5a + 4 = 0, a = -4, a = -1$.
При $x = a$ должно выполняться равенство $a^2 - 4a^2 - a + 4a^2 + 4a - 4 = 0, a^2 + 3a - 4 = 0, a = 1, a = -4$.
При $a = -1, a = 1$ исходное уравнение имеет единственный корень.
При $а=-4$, $D>0$ и корни $х=-4$ и $х=а$ совпадают, поэтому это значение параметра также подходит
Задача 2
Найдите все целые значения параметра $a$, при каждом из которых уравнение $(ax-2-x)(3x^5+7x^3+2x+4-3x^2a-a)=0$ имеет хотя бы один целый корень.
Решение
Рассмотрим два случая:
1) $ax - 2 - x = 0$; при $x ≠ 0$ получим $a = {2 + x}/{x} = 1 + {2}/{x}$.
Так как по условию $a$ и $x$ целые числа, то ${2}/{x}$ тоже целое число. Это возможно, если $x = ±1$ или $x = ±2$.
$x = 1; a - 2 - 1 = 0; a = 3;$
$x = -1; -a - 2 - (-1) = 0; a = -1;$
$x = 2; 2a - 2 - 2 = 0; a = 2;$
$x = -2; -2a - 2 - (-2); a = 0.$
Если $x = 0$, то $0 - 2 - 0 = 0$ не выполняется.
2) $3x^5 + 7x^3 + 2x + 4 - 3x^2a - a = 0,$
$a(3x^2 + 1) = 3x^5 + 7x^3 + 2x + 4,$
$a = {3x^5 + 7x^3 + 2x + 4}/{3x^2 + 1}$
$a = x^3 + 2x + {4}/{3x^2 + 1}$. Поскольку $a$ и $x$ - целые числа, то ${4}/{3x^2 + 1}$ также целое число. Это возможно, если $3x^2 + 1 = 4$, или $3x^2 + 1 = 2$, или $3x^2 + 1 = 1$.
Получаем $x^2 = 1$ или $3x^2 = 1$ или $x^2 = 0$.
Целые корни:
$x = 1$, тогда $a = 1^3 + 2·1 + {4}/{3·1^2 + 1} = 4$;
$x = -1$, тогда $a = (-1)^3 + 2·(-1) + {4}/{3·(-1)^2 + 1} = -2$;
$x = 0$, тогда $a = 0 + 0 + 4 = 4$.
Целые корни есть при значениях $a: -2; -1; 0; 2; 3; 4$.
Задача 3
Найдите все значения параметра $a$, при каждом из которых система уравнений $\{{\table {y=a-x{,}}; {|x-2|(y+5x-10)=(x-2)^3};}$ имеет ровно четыре различных решения.
Решение
При замене $y + x = t$ получим систему уравнений $\{{\table t=a; {|x - 2|(t + 4x - 10) = (x - 2)^3};}$ которая имеет, столько же решений, что и заданная система.
График первого уравнения системы $t = a$ представляет собой прямую, параллельную оси абсцисс.
Построим график второго уравнения.
1) При $x ≥ 2$ получим $(x - 2)(t + 4x - 10) = (x - 2)^3$,
$(x - 2)(t + 4x - 10 - (x - 2)^2) = 0$,
$(x - 2)(t - x^2 + 8x - 14) = 0$,
$x - 2 = 0$ или $t - x^2 + 8x - 14 = 0$.
$x = 2$ — вертикальная прямая.
$t = x^2 - 8x + 14$ — парабола с вершиной $(4; -2), t(2) = 2$.
2) При $x < 2$ получим $-(x - 2)(t + 4x - 10) = (x - 2)^3$,
$(x - 2)(t + 4x - 10 + (x - 2)^2) = 0$.
$x - 2 = 0$ не выполняется при $x < 2$.
$t + 4x - 10 + (x - 2)^2 = 0, t = -x^2 + 6$ — парабола с вершиной $(0; 6), t(2) = 2$.
На рисунке изображен график второго уравнения полученной системы.
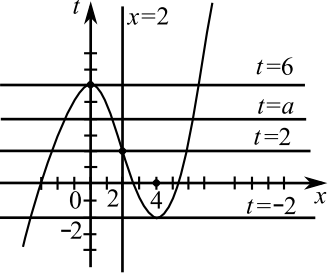
График прямой $t = a$ и уравнения $|x - 2|(t + 4x - 10) = (x - 2)^3$ имеют ровно $4$ общие точки при $-2 < a < 2, 2 < a < 6$.
Задача 4
Найдите все целые значения параметра $a$, при каждом из которых уравнение $(ax-2x+3)(4x^6-19x^4-x^2(5+4a)-a-17)=0$ имеет хотя бы один целый корень.
Решение
Рассмотрим два случая:
1) $ax - 2x+3 = 0$; при $x = 0$ получим $3=0$, это не верно.
При $x ≠ 0, a = {2x - 3}/{x}, a = 2 - {3}/{x}$.
По условию числа $a$ и $x$ целые, поэтому число ${3}/{x}$ тоже целое, что возможно при $x = ±1, x = ±3$.
При $x = 1$ получим $a = -1$,
при $x = -1$ получим $a = 5$,
при $x = 3$ получим $a = 1$,
при $x = -3$ получим $a = 3$.
2) $4x^6 - 19x^4 - 5x^2 - 4ax^2 - a - 17 = 0$,
$a(4x^2 + 1) = 4x^6 - 19x^4 - 5x^2 - 17$,
$a = {4x^6 - 19x^4 - 5x^2 - 17}/{4x^2 + 1}$.
$a = x^4 -5x^2 - {17}/{4x^2 + 1}$. Так как $a$ и $x$ - целые числа, то ${17}/{4x^2 + 1}$ тоже целое число. Это возможно при $4x^2 + 1 = 1$ или $4x^2 + 1 = 17$.
$x^2 = 0, x = 0, a = 0 - 0 - 17 = -17$;
$x^2 = 4, x = ±2, a = 2^4 - 5·2^2 - {17}/{4·2^2 + 1} = -5$.
Уравнение имеет хотя бы один целый корень при значениях $a$, равных $-17; -5; -1; 1; 3; 5$.
Задача 5
При каком значении $a$ множеством решений неравенства
${1+3^x} / {1+3^{-x}}>{3} / {|x+a|}$ является множество всех положительных чисел?
Решение
Сократив левую часть неравенства на $1 + 3^x$, получим равносильное неравенство $3^x > {3}/{|x + a|}$ или $3^{x-1} > {1}/{|x + a|}$. Так как обе части неравенства положительны, то ${1}/{3^{x-1}} < |x + a| (x ≠ -a)$ или $({1}/{3})^{x-1} < |x + a|$.
Графиком функции $y = ({1}/{3})^{x-1}$ является график функции $y = ({1}/{3})^x$ сдвинутый на $1$ единицу вправо вдоль оси $Ox$. Графиком функции $y = |x + a|$ является график функции $y = |x|$, сдвинутый вдоль оси $Ox$ в зависимости от величины и знака числа $a$. Учитывая, что $x ≠ -a$, точка $(-a; 0)$ на графиках функций $y = |x + a|$ выколота.
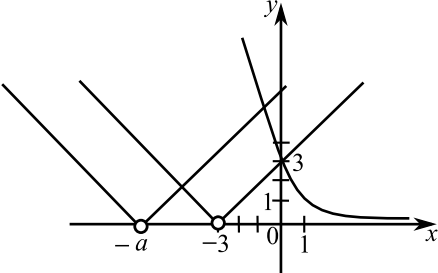
Множество положительных чисел будет решением этого неравенства, если точка пересечения обоих графиков лежит на оси $Oy$. Это произойдет при $a = 3$. Графическая иллюстрация приведена на рисунке.
Задача 6
Найдите все значения $a$, при которых система уравнений
$\{\table\(x-3)^2=(y-1)^2; \(x-a)^2+(y-1)^2=3a^2-8a+9;$
имеет ровно три решения.
Решение
Уравнение $(x - 3)^2 = (y - 1)^2$ равносильно совокупности двух уравнений
$\[\table\ x-3=y-1; \x-3=-y+1;$ $\[\table\ y=x-2; \y=-x+4;$
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x - 2$ и $y = -x + 4$. Заметим, что эти прямые проходят через точку $(3; 1)$, так как система $\{\table\ y = x - 2; \ y = -x + 4;$ имеет единственное решение $(3; 1)$.
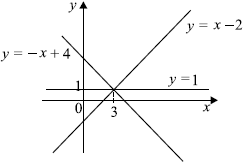
При каждом значении $a$ множеством решений второго уравнения системы $(x - a)^2 + (y - 1)^2 = 3a^2 - 8a + 9$ будет множество всех точек окружности с центром в точке $(a; 1)$, лежащей на прямой $y = 1$, и радиусом $√{3a^2 - 8a + 9}$ (заметим, что $3a^2 - 8a + 9 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
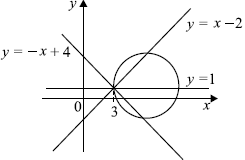
В таком случае точка $(3; 1)$ лежит на окружности, значит, верно равенство $(3 - a)^2 + (1 - 1)^2 = 3a^2 - 8a + 9$.
Отсюда получаем: $9 - 6a + a^2 = 3a^2 - 8a + 9; 2a^2 - 2a = 0; 2a ·(a - 1) = 0; a = 0$ или $a = 1$.
Задача 7
Найдите все значения $a$, при каждом из которых уравнение ${x-3a}/{x+3}+{x-2}/{x-a}=1$ имеет единственный корень.
Решение
${(x - 3a)(x - a) + (x + 3)(x - 2)-(x + 3)(x - a)}/{(x + 3)(x - a)} = 0$,
${x^2 - ax - 3ax + 3a^2 + x^2 + x - 6 - x^2 + ax - 3x + 3a}/{(x + 3)(x - a)} = 0$,
${x^2 - x(3a + 2) + 3a^2 + 3a - 6}/{(x + 3)(x - a)} = 0$.
$\{\table\x^2 - x(3a + 2) + 3a^2 + 3a - 6 = 0; \(x + 3)(x - a) ≠ 0;$
Решим уравнение $x^2 - x(3a + 2) + 3a^2 + 3a - 6 = 0$,
$x_{1,2}={(3a + 2)±√{-3a^2 + 28}}/{2}$.
1. При $D < 0$ уравнение корней не имеет.
2. При $D = 0$ $-3a^2 + 28 = 0, a =±2√{{7}/{3}}$. Уравнение имеет единственный корень $x = {3a + 2}/{2}$ при $a =±2√{{7}/{3}}$.
Проверим условие $x ≠ -3, x ≠ a$.
${3a + 2}/{2} = -3, a = -{8}/{3}≠±2√{{7}/{3}}$,
${3a + 2}/{2} = a, a = -2≠ ±2√{{7}/{3}}$.
Значит, $a=±2√{{7}/{3}}$ удовлетворяет условию.
3. При $D > 0$ уравнение имеет два корня $x_{1,2} ={(3a + 2)±√{28 - 3a^2}/{2}$. Проверим, при каких значениях $a$ значения $x = -3$ и $x = a$ являются корнями уравнения $x^2 - x(3a + 2) + 3a^2 + 3a - 6 = 0$.
При $x = -3$ должно выполняться равенство $9 + 3(3a + 2) + 3a^2 + 3a - 6 = 0, 3a^2 + 12a + 9 = 0, a^2 + 4a + 3 = 0, a = -1, a = -3$.
При $x = a$ должно выполняться равенство $a^2 - 2a + 3a - 6 = 0, a^2 + a - 6 = 0, a_1 = -3, a_2 = 2$.
При $a = -3, a = -1$ и $a = 2$ исходное уравнение имеет единственный корень.
Задача 8
Найдите все значения a, при каждом из которых система неравенств $\{\table\(a - x^2)(a + x - 2) < 0; \x^2 ≤ 1;$ не имеет решений.
Решение
Изобразим множество решений первого неравенства на координатной плоскости $Oxa$, используя метод областей.
1) Пусть $F(x; a) = (a - x^2)(a + x - 2)$.
2) Выражение $F(x; a)$ определено при всех действительных значениях $a$ и $x$.
3) Найдём нули: $F(x; a) = 0$.
$(a - x^2)(a + x - 2) = 0; a - x^2 = 0$ или $a + x - 2 = 0; a = x^2$ или $a = -x + 2$.
4) Построим параболу $a = x^2$ и прямую $a = -x + 2$ (пунктирными линиями) в системе координат $Oxa$.
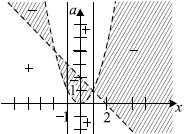
Далее определяем знак значения выражения $F(x; a)$ в одной из областей $F(0; 1) < 0$, затем расставляем знаки в других областях, используя правило знакочередования. Области, выделенные знаком "минус", представляют графически множество решений первого неравенства.
Второе неравенство системы $x^2 ≤ 1$ или $(x - 1)(x + 1) ≤ 0$ задаёт на координатной плоскости $Oxa$ вертикальную полосу вместе с границами $x = -1$ и $x = 1$. Множества решений первого и второго неравенств системы на плоскости $Oxa$ не имеют общих точек при $a ∈ (-∞; 0]∪[3;+∞)$.
Задача 9
Найдите все значения параметра $a$, при каждом из которых система уравнений $\{\table\y=√{-7-8x-x^2}; \y-ax=3-a;$ имеет единственное решение.
Решение
Построим график уравнения $y = √{−7−8x−x^2}$.
Преобразовав подкоренное уравнение, получим: $y = √{9−(x^2 + 8x + 16)}, y = √{3^2 −(x + 4)^2}$.
Если $y ≥ 0$, то $y^2 = 9−(x + 4)^2, (x + 4)^2 + y^2 = 9$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность радиусом $3$ с центром в точке $(−4;0)$, лежащая в верхней полуплоскости.
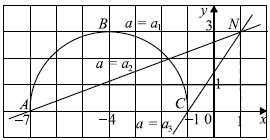
Уравнение $y − ax = 3 − a$ запишем в виде $y = a(x −1) + 3$ — семейство прямых с угловым коэффициентом $a$, проходящих через точку $N(1;3)$.
Рассмотрим рисунок. Видно,что прямая и полуокружность имеют две общие точки, если:
1) прямая касается полуокружности, при этом $a = a_1 = 0$,
2) прямая и полуокружность имеют единственную общую точку, при этом $a_2 < a ≤ a_3$.
Найдём $a_2$ из условия, что прямая $y = a(x−1) + 3$ проходит через точку $A(−7;0)$.
$a(−7−1) + 3 = 0, a = {3}/{8}$, значит, $a_2 = {3}/{8}$.
Найдём $a_3$ из условия, что прямая $y = a(x−1) + 3$ проходит через точку $C(−1;0)$.
$a(−1−1) + 3 = 0, a = {3}/{2}$, значит, $a_3 = {3}/{2}$.
Имеем ${3}/{8} < a ≤ {3}/{2}$.
Система имеет единственное решение, если ${3}/{8} < a ≤ {3}/{2}$ и $a = 0$.
Задача 10
Найдите все значения $a$, при которых система уравнений
$\{\table\y=√{-5-6x-x^2}; \y-ax=2-3a;$
имеет ровно два решения.
Решение
Построим график уравнения $y = √{-5 - 6x - x^2}$,
Преобразовав подкоренное выражение, получим $y = √{4 - (x^2 + 6x + 9)}, y = √{2^2 - (x + 3)^2}$.
Если $y ≥ 0$, то $y^2 = 2^2 - (x + 3)^2, (x + 3)^2 + y^2 = 2^2$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность с центром в точке $(-3; 0)$ радиусом $2$, лежащая в верхней полуплоскости.
Уравнение $y-ax = 2-3a$ запишем в виде $y = a(x-3)+2$ - семейство прямых с угловым коэффициентом $a$, проходящих через точку $M (3; 2)$.
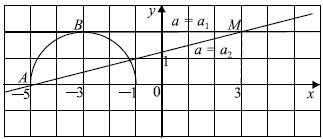
Рассмотрим рисунок. Видно, что прямая и полуокружность имеют две общие точки, если $a_1 < a ≤ a_2$. Прямая $BM$ касается окружности и является горизонтальной, поэтому её угловой коэффициент равен $0$, значит, $a_1 = 0$. Найдём $a_2$ из условия, что прямая $AM$ $y = a(x - 3) + 2$ проходит через точку $A(-5; 0)$.
$a(-5 - 3) + 2 = 0, a = {1}/{4}$, значит, $a_2 = {1}/{4}$.
Следовательно, система имеет ровно два решения при $0 < a ≤ {1}/{4}$.
Задача 11
Найдите все значения $a$, при каждом из которых система уравнений $\{\table\(xy^2-5xy-5y+25)/{√{x+5}}=0; \y=ax;$ имеет ровно два различных решения.
Решение
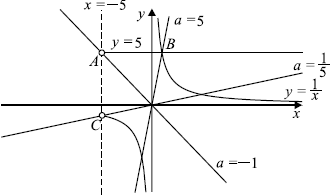
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение ${xy^2 - 5xy - 5y + 25}/{√{x + 5}}= 0$ параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде ${(y - 5)(xy - 5)}/{√{x + 5}} = 0$, разложив числитель на множители.
При $x ≤ -5$ первое уравнение системы не имеет смысла. При $x > -5$ уравнение задаёт прямую $y = 5$ и гиперболу $y ={5}/{x}$.
Число решений исходной системы равно числу точек пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$ с прямой $y = ax$ при условии $x>-5$.
Найдём координаты точек $A, B$ и $C$.
$B$ - точка пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$, чтобы найти её координаты, нужно решить систему уравнений $\{\table\y = 5; \y ={5}/{x};$
Получаем $B(1; 5)$.
У точек $A$ и $C$ абсцисса равна $-5$, ординаты находим из уравнений прямой и гиперболы. $A(-5; 5)$ и $C(-5;-1)$.
При каждом значении $a$ уравнение $y = ax$ задаёт прямую с угловым коэффициентом $a$, проходящую через начало координат. Чтобы найти значение $a$, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
Например, для точки $A(-5; 5)$ получаем $x = -5; y = 5; 5 = a·(-5); a = -1$. Аналогично для $B(1; 5)$ получим $a = 5$. Для $C(-5;-1)$ получим $a ={1}/{5}$.
При $x>-5$ прямая $y = ax$ пересекает прямую $y = 5$ при $a<-1$ и $a>0$, пересекает правую ветвь гиперболы $y ={5}/{x}$ при $a>0$, пересекает левую ветвь гиперболы $y ={5}/{x}$ при $a>{1}/{5}$. При этом прямая $y = ax$ проходит через точку пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$ при $a = 5$.
Таким образом, исходная система имеет ровно два решения при $0< a ≤0.2; a = 5$.
Задача 12
Найдите все значения $a$, при каждом из которых уравнение ${3x + a - x^2 + 4a^2x - x^3}/{4a^2x - x^3} = 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
${3x + a - x^2 + 4a^{2}x - x^3}/{4a^{2}x - x^3} = {4a^{2}x - x^3}/{4a^{2}x - x^3} + {-x^2 + 3x + a}/{4a^{2}x - x^3} = 1 + {-x^2 + 3x + a}/{4a^{2}x - x^3}$.
Тогда уравнение примет вид ${-x^2 + 3x + a}/{4a^{2}x - x^3} = 0$. Оно равносильно системе
$\{\table\ -x^2 + 3x + a = 0; \4a^{2}x - x^3 ≠ 0;$ $\{\table\ a = x^2 - 3x; \ x ≠ 0, x ≠ ±2a;$
Решим систему графически в системе координат $xOa$. Для этого строим графики функций $a = x^2 - 3x$ и $a = ±{x}/{2}$.
Графиком функции $a = x^2 - 3x$ является парабола, ветви которой направлены вверх. Вершина параболы - точка $({3}/{2}; -{9}/{4})$, точки $(0; 0)$ и $(3; 0)$ принадлежат параболе. Графиками функций $a = ±{x}/{2}$ являются прямые.
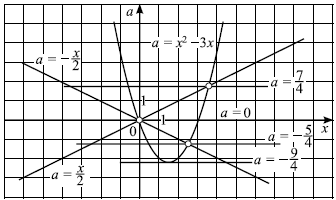
Решая уравнение $x^2 - 3x = {x}/{2}$, находим точки пересечения прямой $a = {x}/{2}$ и параболы $a = x^2 - 3x: x = 0, x = {7}/{2}$, откуда $a = 0, a = {7}/{4}$. Аналогично, решая уравнение $x^2 - 3x = - {x}/{2}$, находим $x = 0, x = {5}/{2}$. Тогда $a = 0, a = - {5}/{4}$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых при $a = - {9}/{4}, a = - {5}/{4}, a = 0, a = {7}/{4}$.
Задача 13
Найдите все значения параметра a, при каждом из которых система уравнений $\{\table\y=√{-8-6x-x^2}; \y+ax=a+1;$ имеет единственное решение.
Решение
Построим график уравнения $y = √{−8−6x−x^2}$.
Преобразовав подкоренное выражение, получим: $y = √{1−(x^2 + 6x + 9)}, y =√{1−(x + 3)^2}$.
Если $y ≥ 0$, то $y^2 = 1−(x + 3)^2, (x + 3)^2 + y^2 = 1$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность радиусом $1$ с центром в точке $(−3;0)$, лежащая в верхней полуплоскости.
Уравнение $y + ax = a + 1$ запишем в виде $y = −a(x−1) + 1$ — семейство прямых с угловым коэффициентом $−a$, проходящих через точку $M(1;1)$.
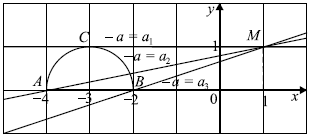
Рассмотрим рисунок. Видно, что система имеет единственное решение, если:
1) прямая $MC$ касается полуокружности, поэтому $−a = a_1 = 0$,
2) прямая и полуокружность имеют единственную общую точку, при этом $a_2 < −a ≤ a_3$.
Найдём $a_2$ из условия, что прямая $y = a_2(x−1) + 1$ проходит через точку $A(−4;0)$.
$a_2(−4−1) + 1 = 0, a_2 ={1}/{5}$.
Найдём $a_3$ из условия, что прямая $y = a_3(x−1) + 1$ проходит через точку $B(−2;0)$.
$a_3(−2−1) + 1 = 0, a_3 ={1}/{3}$.
Имеем ${1}/{5} < −a ≤ {1}/{3}$, значит, $−{1}/{3} ≤ a < −{1}/{5}$.
Следовательно, система имеет единственное решение, если $−{1}/{3} ≤ a < −{1}/{5}$ и $a = 0$.
Задача 14
Найдите все значения $a > 0$, при каждом из которых система
$\{\table\(|x| - 3)^2 + (y - 3)^2 = 4; \(x + 3)^2 + y^2 = a^2;$
имеет единственное решение.
Решение
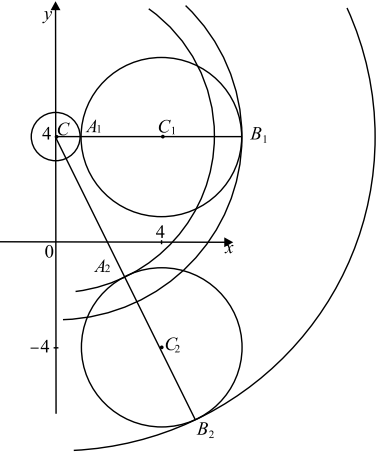
Если $x ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(3; 3)$ радиуса $2$, а если $x < 0$, то оно задаёт окружность $∅_2$ с центром в точке $C_2(−3; 3)$ того же радиуса.
При $a > 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (−3; 0)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет единственную общую точку с объединением окружностей $∅_1$ и $∅_2$.
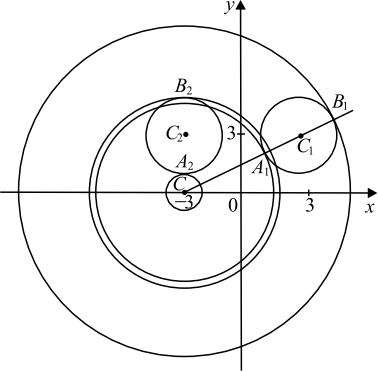
Из точки $C$ проведём луч $CC_1$ и обозначим $A_1$ и $B_1$ точки его пересечения с окружностью $∅_1$, где $A_1$ лежит между $C$ и $C_1$.
Так как $CC_1 = √{6^2 + 3^2} = √{45} = 3√5$, то $CA_1 = 3√5 − 2, CB_1 = 3√5 + 2$.
При $a < CA_1$ или $a > CB_1$ окружности $∅$ и $∅_1$ не пересекаются. При $CA_1 < a < CB_1$ окружности $∅$ и $∅_1$ имеют $2$ общие точки. При $a = CA_1 = 3√5 − 2$ или $a = CB_1 = 3√5 + 2$, окружности $∅$ и $∅_1$ касаются.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_2(−3; 1)$ и $B_2(−3; 5)$. То есть при $a = 1$ и $a = 5$ окружности $∅$ и $∅_2$ касаются. При остальных значениях параметра $a$ окружности $∅$ и $∅_2$ либо имеют $2$ общие точки, либо не имеют общих точек.
Исходная система имеет единственное решение тогда и только тогда, когда окружность $∅$ касается ровно одной из двух окружностей $∅_1$ и $∅_2$ и не пересекается с другой.
Так как $1 < 3√5 − 2 < 5 < 3√5 + 2$, то условию задачи удовлетворяют только числа $a = 1$ и $a = 3√5 + 2$.
Задача 15
Найдите все значения $a$, при каждом из которых уравнение ${x^3 + x^2 - 16a^2x - 5x + a}/{x^3 - 16a^2x}= 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
${x^3 + x^2 - 16a^2x - 5x + a}/{x^3 - 16a^2x} = {x^3 - 16a^2x}/{x^3 - 16a^2x} + {x^2 - 5x + a}/{x^3 - 16a^2x} = 1 + {x^2 - 5x + a}/{x^3 - 16a^2x}$.
Тогда уравнение примет вид ${x^2 - 5x + a}/{x^3 - 16a^2x} = 0$.
Оно равносильно системе
$\{\table\x^2 - 5x + a = 0; \x^3 - 16a^2x ≠ 0;$ $\{\table\a = -x^2 + 5x; \x ≠ 0, x ≠±4a;$
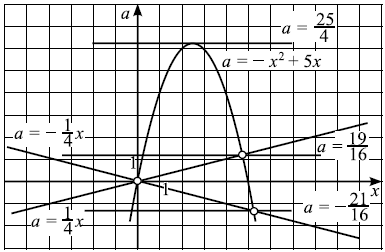
Решим систему графически в системе координат $xOa$. Для этого построим графики функций $a = -x^2 + 5x$ и $a =±{x}/{4}$.
Графиком функции $a = -x^2+5x$ является парабола, ветви которой направлены вниз. Вершина параболы - точка $({5}/{2}; {25}/{4})$, точки (0; 0) и (5; 0) принадлежат параболе. Графиками функций $a =±{x}/{4}$ являются прямые.
Решая уравнение $-x^2 + 5x = {x}/{4}$, находим точки пересечения прямой $a ={x}/{4}$ и параболы $a = -x^2 + 5x: x = 0, x = {19}/{4}$, откуда $a = 0, a = {19}/{16}$. Аналогично, решая уравнение $-x^2 + 5x = -{x}/{4}$, находим $a = 0, a = -{21}/{16}$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых будет при $a = -{21}/{16}, a = 0, a = {19}/{16}; a = {25}/{4}$.
Задача 16
Найдите все значения $a > 0$, при каждом из которых система
$\{\table\(x - 4)^2 + (|y| - 4)^2 = 9; \x^2 + (y - 4)^2 = a^2;$
имеет ровно $2$ решения.
Решение
Если $y ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(4; 4)$ радиуса $3$, а если $y < 0$, то оно задаёт окружность $∅_2$ с центром в точке $C_2(4; -4)$ того же радиуса.
При $a > 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (0; 4)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет ровно две общие точки с объединением окружностей $∅_1$ и $∅_2$.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_1(1; 4)$ и $B_1(7; 4)$. То есть при $a = CA_1=1$ и $a = CB_1=7$ окружности $∅$ и $∅_2$ касаются. При $a > 7$ и $a < 1$ окружности $∅$ и $∅_1$ не пересекаются, при $1 < a < 7$ окружности $∅$ и $∅_2$ имеют $2$ общие точки.
Из точки $C$ проведём луч $CC_2$ и обозначим $A_2$ и $B_2$ точки его пересечения с окружностью $∅_2$, где $A_2$ лежит между $C$ и $C_2$. Заметим, что длина отрезка $CC_2 = √{4^2 + (4-(-4))^2} = √{80} = 4√5$.
При $a < CA_2$ или $a > CB_2$ окружности $∅$ и $∅_2$ не пересекаются. При $CA_2 < a < CB_2$ окружности $∅$ и $∅_2$ имеют $2$ общие точки. При $a = CA_2 = 4√5 − 3$ или $a = CB_2 = 4√5 + 3$, окружности $∅$ и $∅_2$ касаются.
Исходная система имеет ровно 2 решения тогда и только тогда, когда окружность $∅$ с одной из окружностей $∅_1$ и $∅_2$ имеет $2$ общие точки, а с другой не пересекается, либо касается одновременно двух окружностей.
Так как $1 < 4√5 − 3 < 7 < 4√5 + 3$, то условию задачи удовлетворяют значения $a ∈ (1; 4√5 − 3) ∪ (7; 4√5 + 3).$.
Задача 17
Найдите все значения $a$, при которых система уравнений
$\{\table\y=√{5+4x-x^2}; \y-ax=4a+3;$
имеет ровно два решения.
Решение
Построим график уравнения $y = √{5 + 4x - x^2}$. Преобразовав подкоренное выражение, получим: $y = √{9 - (x^2 - 4x + 4)}, y = √{3^2 - (x - 2)^2}$.
Если $y ≥ 0$, то $y^2 = 3^2 - (x - 2)^2, (x - 2)^2 + y^2 = 3^2$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность с центром в точке $(2; 0)$ радиусом $3$, лежащая в верхней полуплоскости.
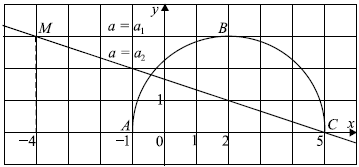
Уравнение $y - ax = 4a + 3$ запишем в виде $y = a(x + 4) + 3$ - семейство прямых с угловым коэффициентом $a$, проходящих через точку $M(-4; 3)$.
Рассмотрим рисунок. Видно, что прямая и полуокружность имеют две общие точки, если $a_2 ≤ a < a_1$. Прямая $BM$ касается окружности, её угловой коэффициент равен $0$, значит, $a_1 = 0$. Найдём $a_2$ из условия, что прямая $MC$: $y = a(x + 4) + 3$ проходит через точку $C(5; 0)$, то есть $y(5) = 0$.
$a(5 + 4) + 3 = 0, a = -{1}/{3}$, значит, $a_2 = -{1}/{3}$.
Значит, система имеет ровно два решения при $-{1}/{3} ≤ a < 0$.
Задача 18
Найдите все значения параметра $a$, при которых уравнение $√ {a - 2xy} = y - x + 5$ имеет единственное решение.
Решение
$√{a-2xy}=y-x+5$
ОДЗ:$\{\table\y≥x-5; \a ≥ 2xy;$
$a-2xy=y^2+x^2+5^2-2xy+2·5y-2·5·x$
$a=x^2+y^2+10y-10x+25$
$a=(x-5)^2+(y+5)^2-25$
$(x-5)^2+(y+5)^2=a+25$ - уравнение окружности с центром в т.О(5;-5) и радиусом R; $R^2=a+25$

Уравнение имеет единственное решение на ОДЗ, если окружность будет касаться прямой $y=x-5$, в т.А(${5}/{2}; -{5}/{2}$), тогда
$OA=R; OA={5√2}/{2}; R={5√2}/{2}$
$a+25=R^2$
$a+25=({5√2}/{2})^2$
$a+25={25}/{2}$
$a={25}/{2}-25$
$a=-12.5$
Проверка: $-12.5 ≥ 2·{5}/{2}·(-{5}/{2})$
$-12.5 ≥ -12.5$
Рекомендуемые курсы подготовки

- Получишь все формулы, которые нужны для решения ЛЮБОЙ задачи по теории вероятностей в ЕГЭ по профилю
- Научишься решать задачи №4.5 в ЕГЭ по профилю
- Улучшить свой результат на +15 вторичных баллов
на бесплатном курсе Турбо ЕГЭ

