Задание 16. Окружность, круг и их элементы. ОГЭ 2026 по математике
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
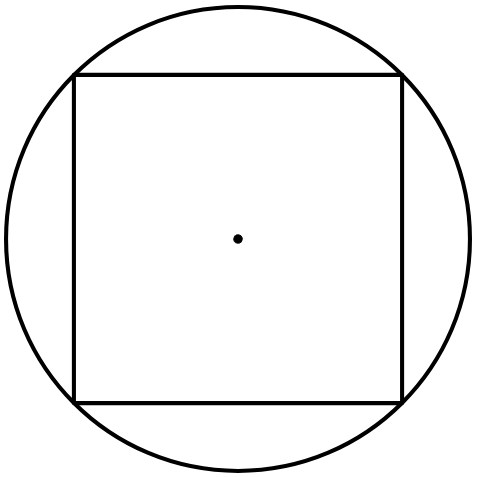
Сторона квадрата равна 38√2 . Найдите радиус окружности, описанной около этого квадрата.
Решение
В квадрате все стороны между собой равны, значит: $AB = BC = CD = DA = 38√2 (см).$
Необходимо по условию задачи найти радиус окружности, описанной около квадрата ABCD.
Используем формулу для нахождения диагонали AC квадрата ABCD:
$ AC = AB√2 = 38√2 × √2 = 76 (см).$
Диагональ квадрата равна диаметру круга.
Найдём радиус круга по формуле:
$AO = {AC} / {2} = 76 / 2 = 38 (см)$.
Задача 2
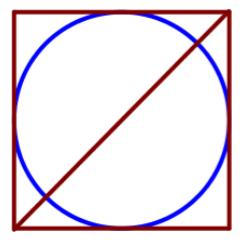
Радиус вписанной в квадрат окружности равен 18 √2 . Найдите диагональ этого квадрата.
Решение
Радиус равен половине стороны квадрата => вся сторона - 36√2
По теореме Пифагора найдем диагональ (d):
$(36√2)^2+(36√2)^2=d^2 $
$ 2592+2592=d^2 $
$d^2=5184 $
$d=72 $
Задача 3
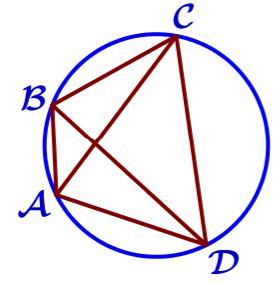
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 120°, угол CAD равен 74°. Найдите угол ABD. Ответ дайте в градусах.
Решение
Угол CAD и угол CBD - вписанные углы, опирающиеся на одну дугу, а значит, они равны 74 градуса
$∠ABD=∠ABC-∠CBD=120°-74°=46°$
Ответ: 46.
Задача 4

Периметр треугольника равен 140, одна из сторон равна 56, а радиус вписанной в него окружности равен 9. Найдите площадь этого треугольника.
Решение
Формула для определения площади треугольника: $S=pr$, где p-полупериметр, r - радиус
Найдем полупериметр (это периметр поделить на 2): $p={140}/{2}=70$ Подставим в формулу площади: $S=70 · 9 = 630$Задача 5

Радиус окружности,описанной около равностороннего треугольника равен 7√3. Найдите длину стороны этого треугольника.
Решение
Воспользуемся формулой радиуса описанной окружности: $R={a√3}/{3}$, где а - сторона треугольника
Подставим туда наш радиус окружности: ${7√3}/{1}={a√3}/{3}$
Перемножим крест на крест (пропорция): $7√3·3=a√3·1$
Получим: $21√3=а√3$
Поделим обе части уравнения на $√3$: а=21
Сторона треугольника равна 21
Задача 6
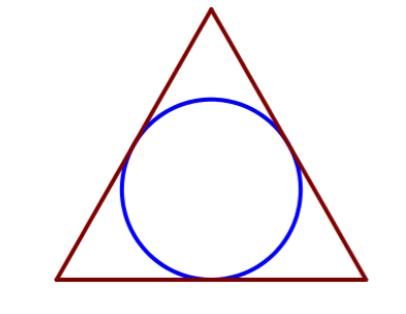
Радиус окружности, вписанной в равносторонний треугольник, равен 9√3 . Найдите длину стороны этого треугольника.
Решение
Воспользуемся формулой радиуса вписанной окружности: $r={a√3}/{6}$, где а - сторона треугольника
Подставим туда наш радиус окружности: ${9√3}/{1}={a√3}/{6}$
Перемножим крест на крест (пропорция): $9√3 · 6= a√3· 1$
Получим: 54√3=a√3
Поделим обе части уравнения на $√3$: a=54
Сторона треугольника равна 54
Задача 7
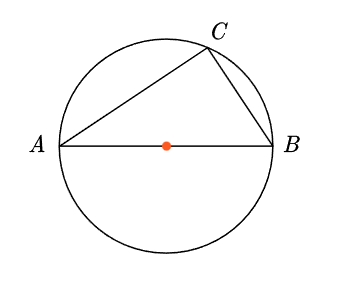
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 14,5. Найдите AC, если BC=21.
Решение
1. Так как центр окружности, описанной около треугольника АВС, лежит на стороне АВ, то АВ – это диаметр описанной окружности:
D = 2R, где R – радиус описанной окружности.
D = 2·14,5 = 29.
АВ = D = 29.
2. Угол С треугольника АВС опирается на диаметр, а вписанный угол, который опирается на диаметр равен 90 °. Тогда треугольник АВС – прямоугольный, АВ = 29 – гипотенуза, так как лежи напротив прямого угла, СВ = 21 – катет.
По теореме Пифагора найдем АС:
АС = $√(AB^2 – BC^2)$;
АС = $√(29^2 – 21^2) = √(841 – 441) = √400 = 20.$
Ответ: АС = 20
Задача 8

Сторона равностороннего треугольника равна 14 √3 . Найдите радиус окружности, описанной около этого треугольника.
Решение
Воспользуемся формулой радиуса описанной окружности: $R={a√3}/{3}$, где а - сторона треугольника
Подставим туда длину стороны треугольника: $R={14 √3·√3}/{3}={14·3}/{3}=14$
Радиус равен 14
Задача 9
Окружность с центром в точке $O$ описана около равнобедренного треугольника $ABC$, в котором $AC = BC$ и $∠ACB = 105^°$. Найдите величину угла $COA$. Ответ дайте в градусах.
Решение
Задача 10
В треугольнике $KNP$ известно, что $KN = 8$, $PN = 15$, угол $N$ равен $90^°$ (см. рис.). Найдите радиус окружности, описанной около этого треугольника.
Решение
Задача 11
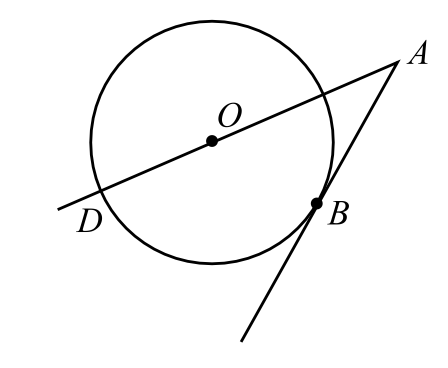
Найдите угол $BAO$, если его сторона $AB$ касается окружности, $O$ — центр окружности, а дуга $BD$ окружности, заключённая внутри этого угла, равна $106^°$ (см. рис.). Ответ дайте в градусах.
Решение
Задача 12
Хорды $MN$ и $PK$ окружности пересекаются в точке $L$, $PL = 32$, $LN = 24$, $KL = 15$. Найдите $ML$.
Решение
Задача 13
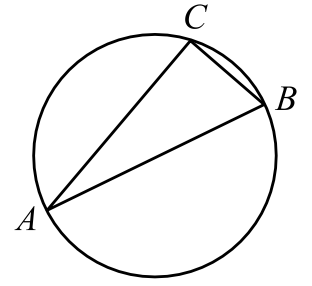
В треугольнике $ABC$ известно, что $AC = 24$, $BC = 7$, угол $C$ равен $90^°$ (см. рис.). Найдите радиус окружности, описанной около этого треугольника.
Решение
Задача 14
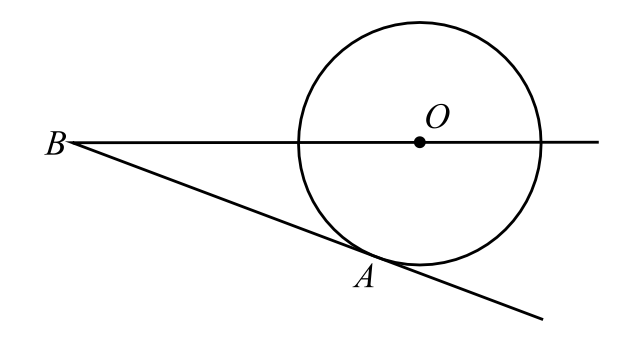
К окружности с центром в точке $O$ проведены касательная $AB$ и секущая $BO$ (см. рис.). Найдите радиус окружности, если $AB = 16$, $BO = 20$.
Решение
Задача 15
Радиус окружности с центром $O$ равен $61$, длина хорды $CB$ равна $120$. Найдите расстояние от хорды $CB$ до параллельной ей касательной $a$, если $a$ и $CB$ расположены по разные стороны от центра окружности.
Решение
Задача 16
Через точку $L$, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке $A$. Другая прямая пересекает окружность в точках $C$ и $D$, причём $LC = 6$, $LD = 24$. Найдите $LA$.
Решение
Задача 17
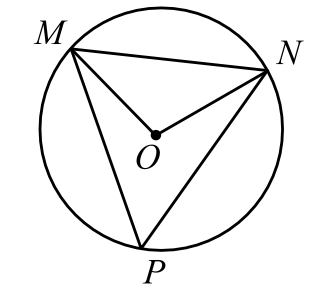
Треугольник $MNP$ вписан в окружность с центром в точке $O$. Точки $O$ и $P$ лежат в одной полуплоскости относительно прямой $MN$ (см. рис.). Найдите угол $MPN$, если угол $MON$ равен $92^°$. Ответ дайте в градусах.
Решение
Задача 18
Радиус окружности с центром $O$ равен $37$, длина хорды $AB$ равна $70$. Найдите расстояние от хорды $AB$ до параллельной ей касательной $a$, если $a$ и $AB$ расположены по разные стороны от центра окружности.
Решение
Задача 19
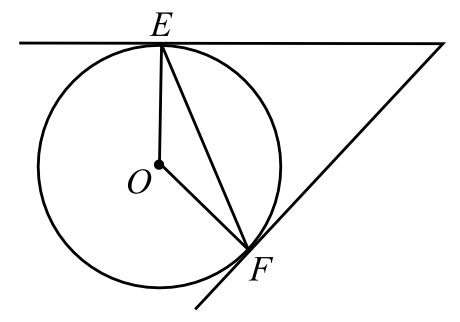
Касательные в точках $E$ и $F$ к окружности с центром $O$ пересекаются под углом $64^°$ (см. рис.). Найдите угол $EFO$. Ответ дайте в градусах.
Решение
Пусть точка пересечения касательных - точка А, тогда угол EAF=64°.
AE перпендикулярна OE, AF перпендикулярна OF (касательная к радиусу)
Рассмотрим треугольник AEF - равнобедренный => $∠AEF=∠AFE= {180°-64°}/{2}={116}/{2}=58°$
Так как $∠AFO=90° => ∠EFO=90°-58°=32°$
Задача 20
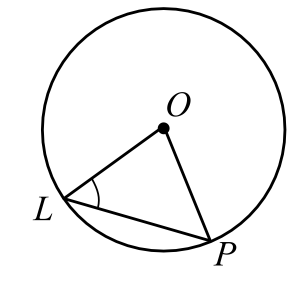
Центральный угол $LOP$ опирается на хорду $LP$ длиной $13$. При этом угол $OLP$ равен $60^°$ (см. рис.). Найдите радиус окружности.
Решение
Рекомендуемые курсы подготовки

- Разберешься в разных типах функций
- Сможешь быстро решать задания №11 ОГЭ и заберешь свой балл за него на экзамене
- Получишь крутую базу для задания №22 из письменной части ОГЭ
- Поймешь, что графики функций не так страшны, как казалось раньше
на бесплатном курсе Турбо ЕГЭ

