Задание 15. Углы, треугольники, четырехугольники, многоугольники и их элементы. ОГЭ 2026 по математике
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
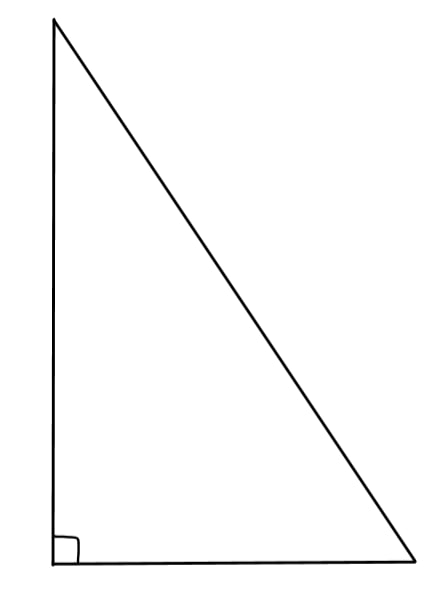
В прямоугольном треугольнике катет и гипотенуза равны 40 и 41 соответственно. Найдите другой катет этого треугольника.
Решение
Пусть искомый катет - это х. По обратной теореме Пифагора, чтобы найти катет, нужно из квадрата гипотенузы вычесть квадрат другого катета, получаем:
$41^2-40^2=x^2$
$1681-1600=x^2$
$x^2=81$
$x=9$
Задача 2

В прямоугольном треугольнике катет и гипотенуза равны 12 и 20 соответственно. Найдите другой катет этого треугольника.
Решение
Пусть искомый катет - это х. По обратной теореме Пифагора, чтобы найти катет, нужно из квадрата гипотенузы вычесть квадрат другого катета, получаем:
$20^2-12^2=x^2$
$400-144=x^2$
$x^2=256$
$x=16$
Задача 3

Катеты прямоугольного треугольника равны 8 и 15 Найдите гипотенузу этого треугольника.
Решение
Пусть гипотенуза - это х. По теореме Пифагора получаем:
$8^2+15^2=x^2$
$64+225=x^2$
$x^2=289$
$x=17$
Задача 4
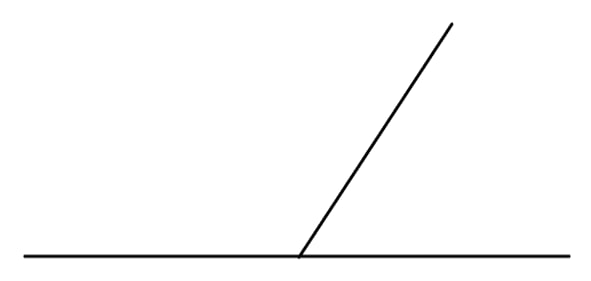
Смежные углы относятся как 2:3. Найдите больший угол.
Решение
1) Находим сколько частей у нас в соотношении: $2+3=5$
2) Так как смежные углы дают в сумме $180^°$, находим сколько градусов будет 1 часть из соотношения: $180^°:5=36^°$
3) Так как больший угол содержит в себе 3 такие части, находим его: $36^°⋅3=108^°$
Задача 5

Катеты прямоугольного треугольника равны 16 и 30. Найдите гипотенузу этого треугольника.
Решение
Пусть гипотенуза - это х. По теореме Пифагора получаем:
$16^2+30^2=x^2$
$256+900=x^2$
$x^2=1156$
$x=34$
Задача 6
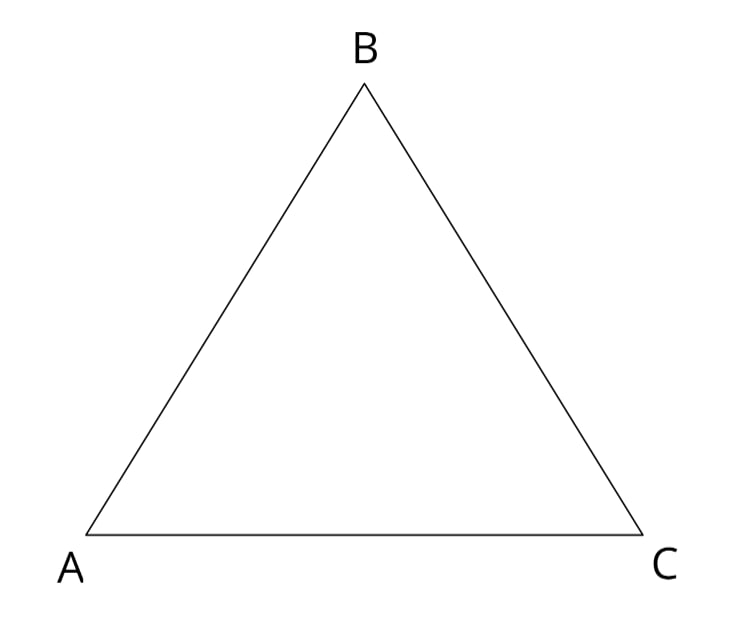
Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
Решение
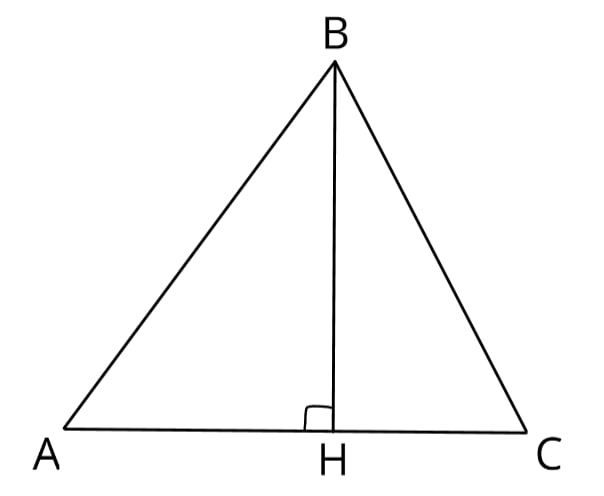
Площадь треугольника можно найти по формуле: $S={1}/{2}·a·h$, где a - сторона, h - высота. Видим, что для формулы нам не хватает высоты, проведем высоту BH. Вспомним, что в равнобедренном треугольнике высота является также медианой и делит AC пополам, значит AH=HC=48:2=24
Рассмотрим прямоугольный треугольник ABH, в нем мы знаем гипотенузу и нижний катет, по теореме Пифагора найдем второй катет:$24^2+x^2=25^2$
$576 + x^2=625$
$x^2=625-576$
$x^2=49$
$x=7 $ - высота
Теперь найдем площадь:
$S={1}/{2}·a·h = {1}/{2}·48·7 = 168$
Задача 7
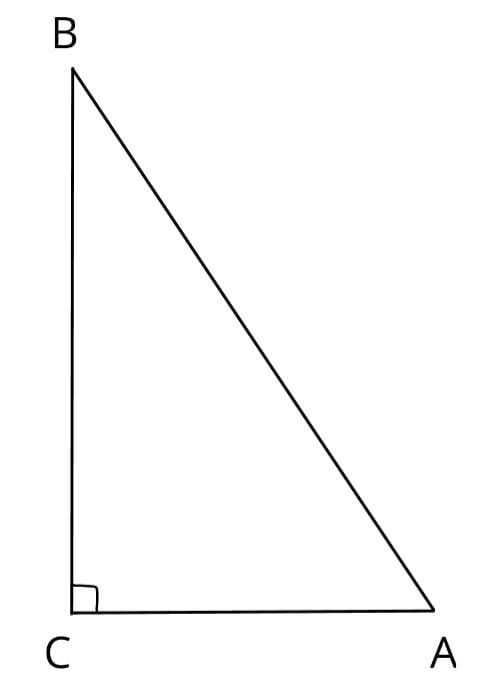
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 15 и 39
Решение
Площадь прямоугольного треугольника можно найти по формуле: $S={1}/{2}·a·b$, где a,b - катеты. Видим, что для формулы нам не хватает катета, обозначим его за x и найдем его по теореме Пифагора:
$15^2+x^2=39^2$
$225+ x^2=1521$
$x^2=1521-225$
$x^2=1296$
$x=36 $ - второй катет
Теперь найдем площадь:
$S={1}/{2}·a·b = {1}/{2}·15·36 = 270$
Задача 8
В треугольнике одна из сторон равна 18, а опущенная на нее высота – 17. Найдите площадь треугольника.
Решение
Площадь треугольника можно найти по формуле: $S={1}/{2}ah$, где a - сторона, h - высота. Подставляем наши данные в формулу, получаем:
$S={1}/{2}ah = {1}/{2} · 18 · 17 = 153$
Задача 9

Диагональ прямоугольника образует угол $63°$ с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Решение
Диагонали прямоугольника в точке пересечения делятся пополам => $OA=OD=OC=OB$
Тогда треугольники AOD, AOB, COB, COD - равнобедренные и их углы при основании равны
$∠OAB=∠OBA=63°$, тогда $∠AOB = 180° - 63° - 63° = 54°$
Задача 10
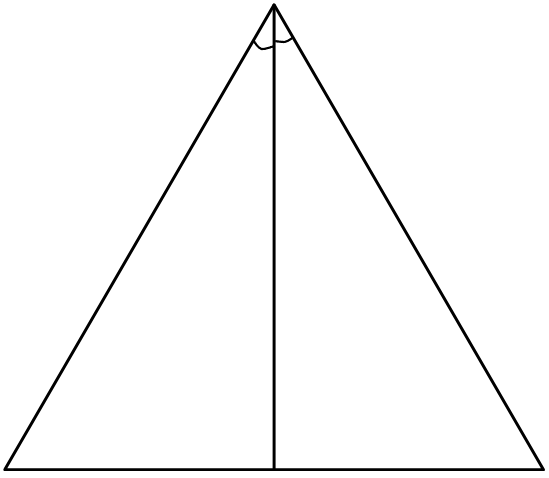
Сторона равностороннего треугольника равна 10√3 . Найдите медиану этого треугольника.
Решение
Медиана равностороннего треугольника является высотой, а значит образует прямоугольный треугольник. Медиана делит основание пополам, а значит половина нижнего основания равна 5√3. Пусть медиана - это x. По теореме Пифагора получаем:
$(5√3)^2+x^2=(10√3)^2 $
$75+x^2=300$
$x^2=300-75$
$x^2=225$
$x=15$
Задача 11

Биссектриса равностороннего треугольника равна 13√3 . Найдите сторону этого треугольника.
Решение
Биссектриса равностороннего треугольника является медианой и высотой, а значит делит основание пополам и образует прямоугольный треугольник. Пусть половина нижнего основания - это x. Тогда сторона треугольника - это 2х. По теореме Пифагора получаем:
$(13√3)^2+x^2=(2x)^2 $
$507+x^2=4x^2$
$x^2-4x^2=-507$
$-3x^2=-507$
$x^2=169$
$x=13$
Так как сторона треугольника - 2х, то 2х=2⋅13=26Задача 12
В треугольнике два угла равны 38° и 89°.Найдите его третий угол. Ответ дайте в градусах.
Решение
Сумма углов треугольника всегда равна 180°, поэтому чтобы найти третий угол нужно вычесть из 180° два известных нам угла: $180-38-89=53$
Задача 13
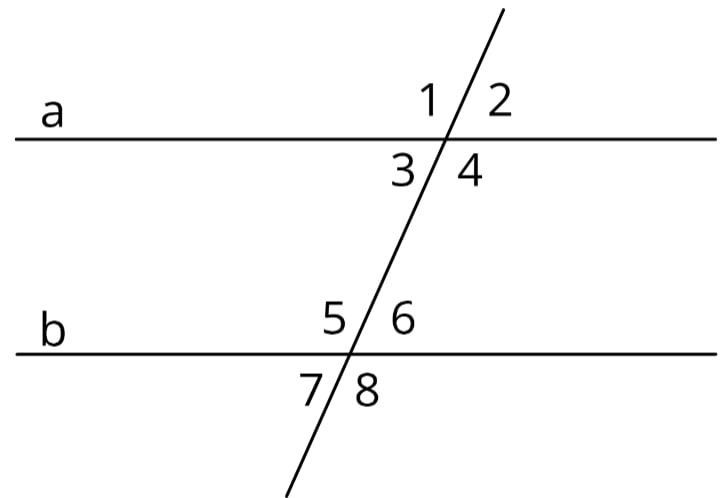
На рисунке прямые а и в параллельны. ∠ 1 на 23 градуса больше ∠ 6. Найдите величину ∠6.
Решение
1) Пусть $∠6 = x$, тогда $∠1 = x+23$
2) $∠1=∠4=x+23$ (как вертикальные углы)
3) Так как ∠4 и ∠6 односторонние, то в сумме они будут давать $180^°$.Составим уравнение:
$∠4+∠6=180$
$x+x+23=180$
$2x=180-23$
$2x=157$
$x=78,5 - ∠6$
Задача 14
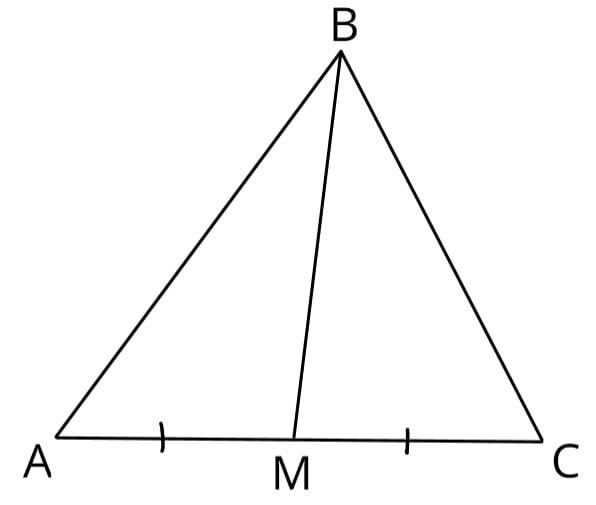
В треугольнике ABC известно, что AC=36, BM – медиана, BM=28. Найдите АM.
Решение
Так как BM - медиана и делит сторону пополам, а нам известна сторона AC, то чтобы найти AM, нужно поделить AC на 2: $AM = 36:2=18$
Задача 15

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой cтороной и основанием равен 45°. Найдите площадь трапеции.
Решение
Для площади не хватает высоты, проведем высоты СH и BF. Найдем AF и HD: $ (9-3):2=3$
Рассмотрим треугольник CHD, в нем мы знаем два угла, найдем третий: $180-90-45=45$ => треугольник CHD - равнобедренный, CH=HD=3, а значит теперь мы знаем высоту и можем найти площадь.
$S={a+b}/{2}∙h= {3+9}/{2}∙3=18$
Задача 16
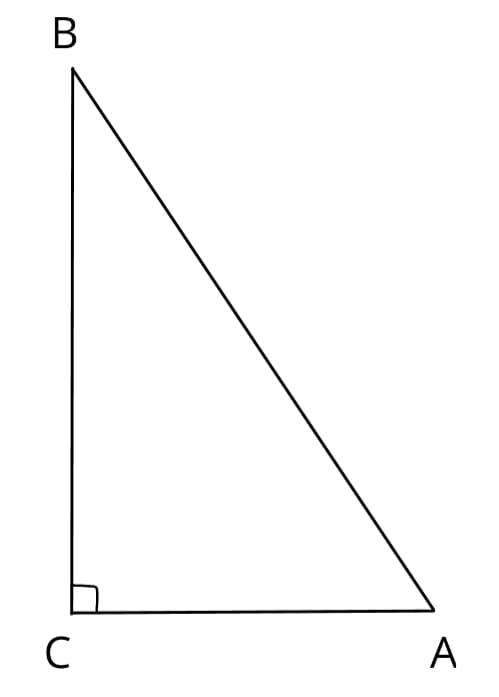
Два катета прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.
Решение
Площадь прямоугольного треугольника можно найти по формуле: $S={1}/{2}ab$, где a,b - катеты. Подставляем наши катеты в формулу, получаем:
$S={1}/{2}ab = {1}/{2} · 18 · 7 = 63$
Задача 17

В треугольнике ABC известно, что AC=16, BM – медиана, BM=12. Найдите АM.
Решение
Так как BM - медиана и делит сторону пополам, а нам известна сторона AC, то чтобы найти AM, нужно поделить AC на 2: $AM = 16:2=8$
Задача 18
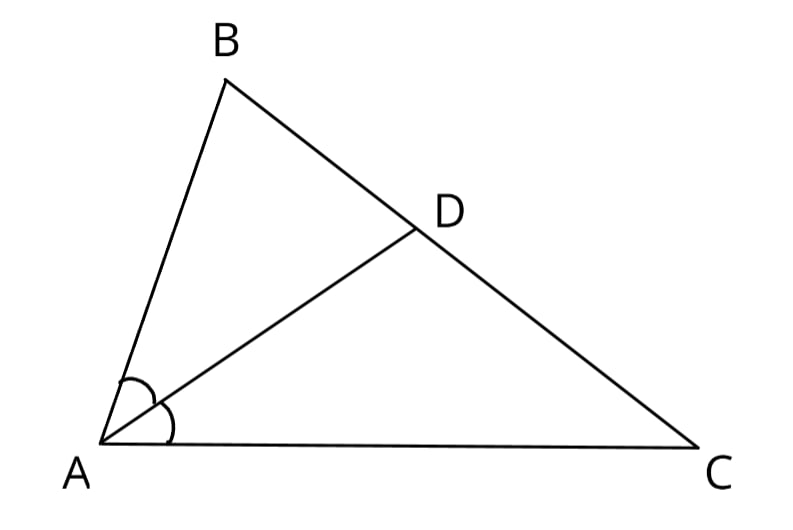
В треугольнике ABC известно, что ∠BAC=82°,AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Решение
Так как AD - биссектриса и делит угол пополам, а нам известен ∠BAC, то чтобы найти ∠BAD, нужно поделить на 2: $∠BAD = 82:2=41$
Задача 19
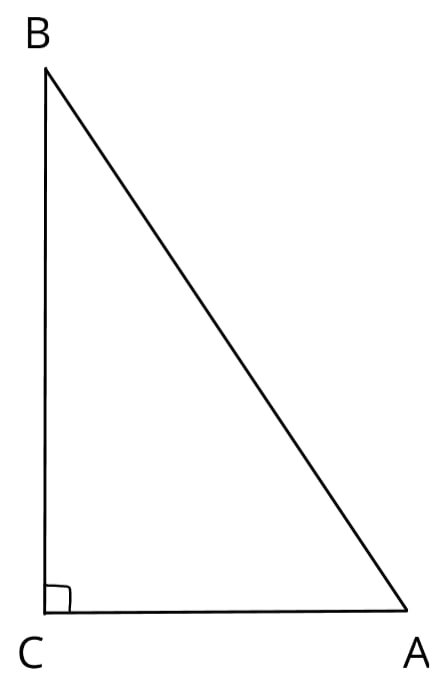
В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.
Решение
Тангенс - это отношение противолежащего катета к прилежащему катету. Противолежащий катет угла B - это AC, прилежащий катет - BC. Нам все известно, находим: $ tgB={AC}/{BC}={28}/{4} = 7 $
Задача 20

В треугольнике ABC известно, что ∠BAC=78°,AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Решение
Так как AD - биссектриса и делит угол пополам, а нам известен ∠BAC, то чтобы найти ∠BAD, нужно поделить на 2: $∠BAD = 78:2=39$
Рекомендуемые курсы подготовки

- Разберешься в разных типах функций
- Сможешь быстро решать задания №11 ОГЭ и заберешь свой балл за него на экзамене
- Получишь крутую базу для задания №22 из письменной части ОГЭ
- Поймешь, что графики функций не так страшны, как казалось раньше
на бесплатном курсе Турбо ЕГЭ

