Задание 22. Функции, графики и их свойства. ОГЭ 2026 по математике
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Постройте график функции $y=|x^2-2x-8|$ и определите, при каких значениях $p$ прямая $y=p$ имеет с графиком функции ровно четыре общие точки.
1. $p=0$
2. $p=9$
3. $p∈(9; +∞)$
4. $p∈(0; 9)$
Решение
Под модулем находится вся квадратичная функция, поэтому достаточно построить график функции $y=x^2-2x-8$ с помощью определения вершины параболы, нулей функции и дополнительных точек и отразить относительно оси Ox:
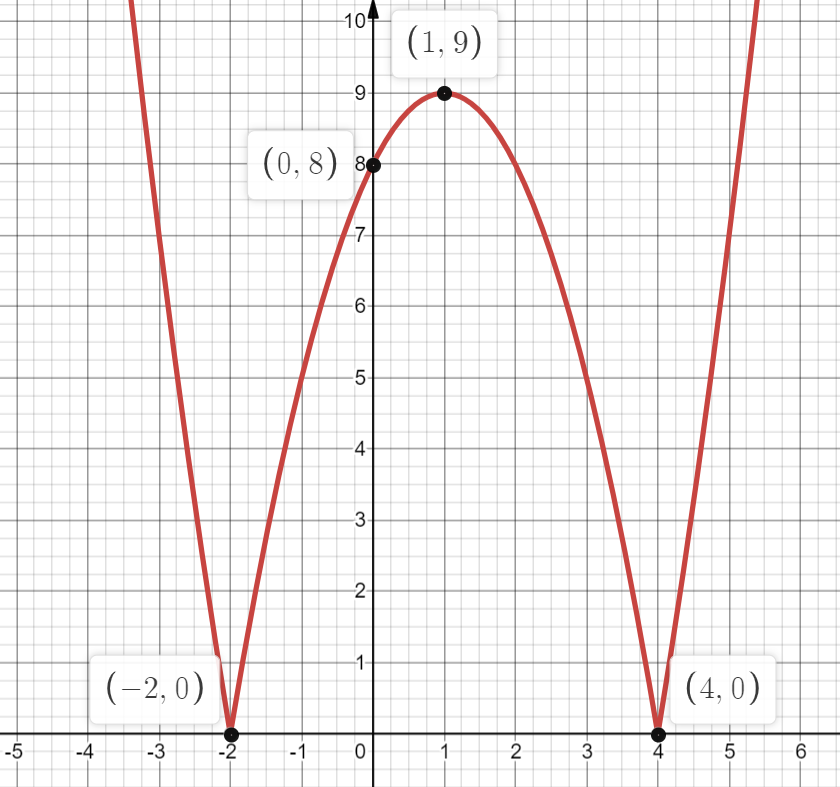
По графику видно, что при $p∈(0; 9)$ прямая $y=p$ имеет с графиком функции ровно четыре общие точки.
Задача 2
Первая прямая проходит через точки с координатами $(3; 1)$ и $(5; 7)$, вторая - через точки $(1; -1)$ и $(5; -5)$. Найдите координату точки пересечения данных прямых. В ответ запишите значение переменной $x$.
Решение
Воспользуемся формулой нахождения уравнения прямой, проходящей через 2 точки, где $(x_1; y_1)$ и $(x_2; y_2)$ - координаты точки, через которые проходит прямая:
${x-x_1}/{x_2-x_1}={y-y_1}/{y_2-y_1}$
1. Первая прямая проходит через точки $(3; 1)$ и $(5; 7)$, подставим в формулу:
${x-3}/{5-3}={y-1}/{7-1} ⇔ {x-3}/{2}={y-1}/{6} ⇔ y=3x-8$ - уравнение 1 прямой
2. Вторая прямая проходит через точки $(1; -1)$ и $(5; -5)$, подставим в формулу:
${x-1}/{5-1}={y-(-1)}/{-5-(-1)} ⇔ {x-1}/{4}={y+1}/{-4} ⇔ y=-x$ - уравнение 2 прямой
3. Чтобы найти точку пересечения прямых, необходимо найти решение системы:
$\{{\table {y=3x-8}; {y=-x}$ $⇔$ $\{{\table {x=2}; {y=-2}$
4. В ответ необходимо записать значение переменной $x$, то есть $2$.
Задача 3
Постройте график функции ${(√{x^2-x-6})^2}/{x+2}$ и определите, при каких значениях $m$ прямая $y=m$ не имеет с графиком данной функции общих точек.
1. $m∈[-5; 0)$
2. $m=-5$
3. $m=0$
4. $m∈(0; +∞)$
В ответ запишите номер верного варианта ответа.
Решение
1.Найдем область определения функции:
$\{{\table {x^2-x-6≥0}; {x+2≠0};}$
Решая первое неравенство методом интервалов и объединяя решения со вторым неравенством, получаем: $x∈(-∞; -2)∪[3; +∞)$
2.Преобразуем выражение:
$y={(√{x^2-x-6})^2}/{x+2}={x^2-x-6}/{x+2}={(x+2)(x-3)}/{x+2}=x-3$
3.Построим график функции $y=x-3$, учитывая область определения:
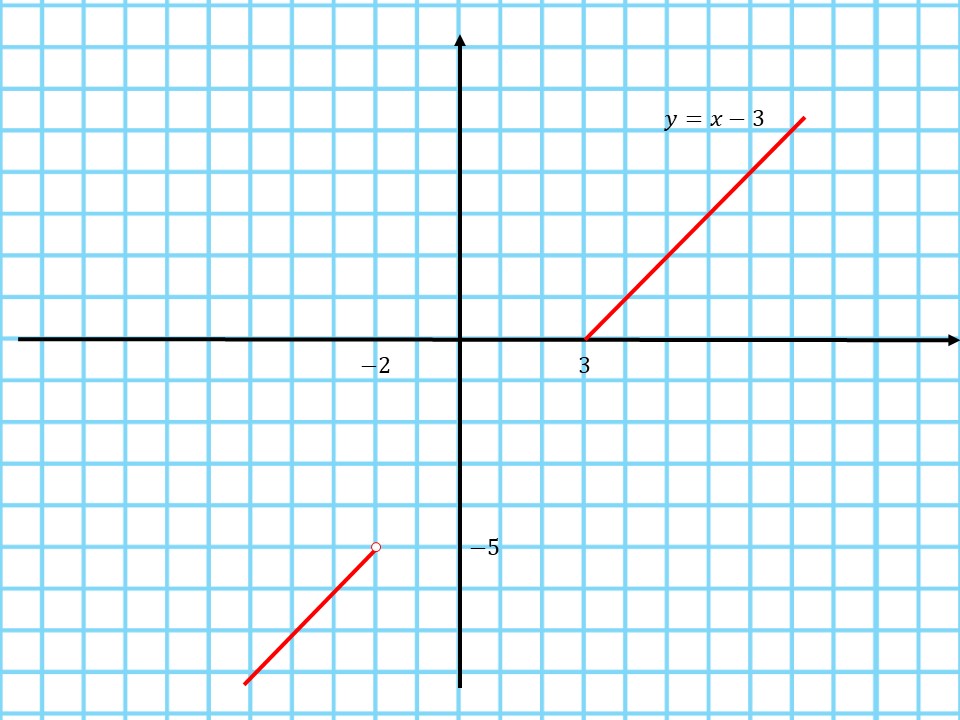
4.Определим, при каких значениях $m$ прямая $y=m$ не имеет с графиком функции общих точек:
Данная прямая - прямая, параллельная оси х. По графику видно, что при $m∈[-5; 0)$ прямая не имеет с графиком общих точек.
Задача 4
Постройте график функции
$y=\{{\table {4x-2, \text ' при 'x<2}; {-x+8, \text ' при ' 2≤x<4}; {2x-4,\text ' при ' x≥4};}$ и определите, при каких значениях $a$ прямая $y=a$ имеет с графиком функции ровно 2 общие точки.
Решение
Данная функция является кусочно-непрерывной, ее график состоит из 3 прямых, которые строятся с помощью таблицы значений при указанных значениях $x$. График функции изображен на рисунке:
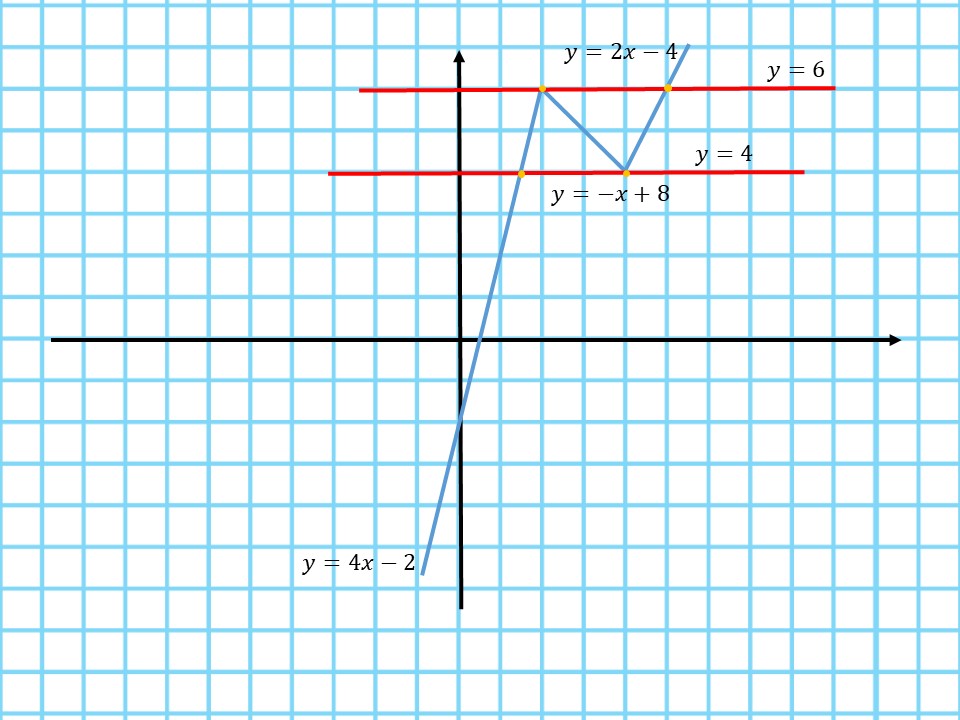
По графику видно, что при $a=4$ и $a=6$ прямая $y=a$, то есть прямая параллельная оси x, имеет с графиком функции две общие точки.
Задача 5
Постройте график функции $y={(x^2-4x+3)(x^2-x-12)}/{x^2-5x+4}$ и определите, при каких значениях $a$ прямая $y=a$ имеет с графиком функции ровно одну общую точку. В ответ запишите наибольшее такое значение.
Решение
1. С помощью формулы $ax^2+bx+c=a·(x-x_1)(x-x_2)$ разложим каждую скобку на множители:
$x^2-4x+3=0 ⇒ x_1=1, x_2=3 ⇒x^2-4x+3=(x-1)(x-3)$
$x^2-x-12=0 ⇒ x_1=-3, x_2=4 ⇒x^2-x-12=(x+3)(x-4)$
$x^2-5x+4=0 ⇒ x_1=1, x_2=4 ⇒x^2-5x+4=(x-1)(x-4)$
2. Преобразуем выражение:
$y={(x^2-4x+3)(x^2-x-12)}/{x^2-5x+4}={(x-1)(x-3)(x+3)(x-4)}/{(x-1)(x-4)}=(x-3)(x+3)=x^2-9$
3. Ограничения: $x^2-5x+4≠0 ⇒ x_1≠1, x_2≠4$
Если $x≠1 ⇒ y≠-8$
Если $x≠4 ⇒ y≠7$
4. Построим график функции $y=x^2-6x+8$ и выколем на нем точки $(1; -8)$ и $(4; 7)$:
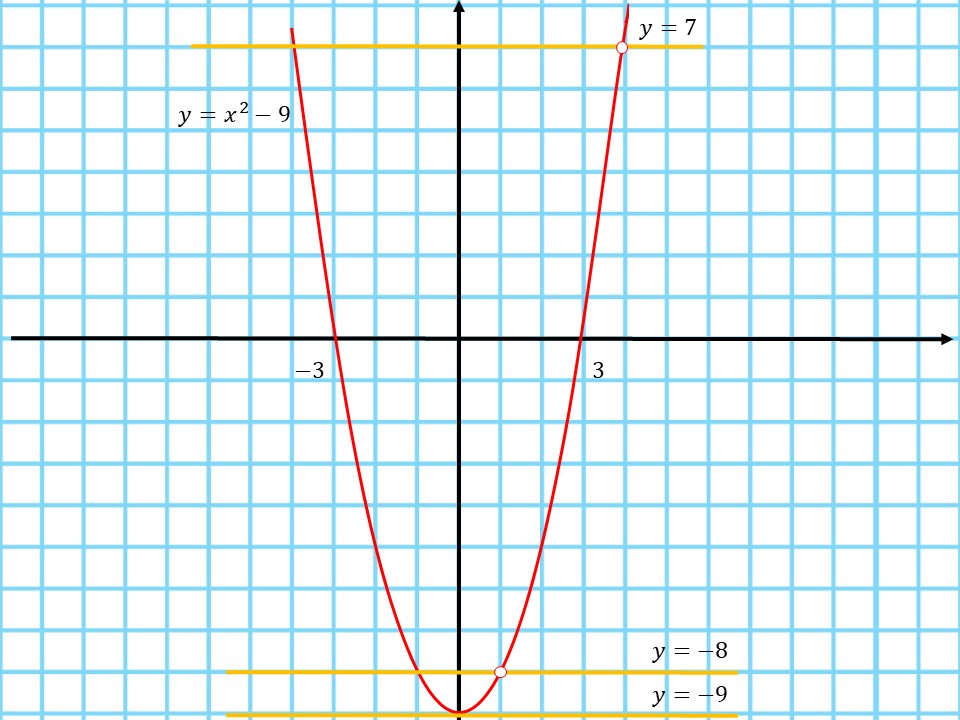
5. По графику видно, что при $a=-9$, $a=-8$ и $a=7$ прямая $y=a$ имеет с графиком функции ровно одну общую точку.
По условию необходимо занимать наибольшее такое значение, то есть $a=-4$.
Задача 6
Первая прямая проходит через точки с координатами $(5; 2)$ и $(8; 5)$, вторая - через точки $(-3; -9)$ и $(0; 3)$. Найдите координату точки пересечения данных прямых. В ответ запишите значение переменной $x$.
Решение
Воспользуемся формулой нахождения уравнения прямой, проходящей через 2 точки, где $(x_1; y_1)$ и $(x_2; y_2)$ - координаты точки, через которые проходит прямая:
${x-x_1}/{x_2-x_1}={y-y_1}/{y_2-y_1}$
1. Первая прямая проходит через точки $(5; 2)$ и $(8; 5)$, подставим в формулу:
${x-5}/{8-5}={y-2}/{5-2} ⇔ {x-5}/{3}={y-2}/{3} ⇔ y=x-3$ - уравнение 1 прямой
2. Вторая прямая проходит через точки $(-3; -9)$ и $(0; 3)$, подставим в формулу:
${x-(-3)}/{0-(-3)}={y-(-9)}/{3-(-9)} ⇔ {x+3}/{3}={y+9}/{12} ⇔ y=4x+3$ - уравнение 2 прямой
3. Чтобы найти точку пересечения прямых, необходимо найти решение системы:
$\{{\table {y=x-3}; {y=4x+3}$ $⇔$ $\{{\table {x=-2}; {y=-5}$
4. В ответ необходимо записать значение переменной $x$, то есть $-2$.
Задача 7
Постройте график функции $y={4x+10}/{4x^2+10x}$ и определите, при каких значениях $k$ прямая $y=kx$ имеет с графиком функции ровно одну общую точку.
Решение
1. Упростим выражение:
$y={4x+10}/{4x^2+10x}={4x+10}/{x(4x+10)}=1/x,$ при $4x+10≠0 ⇒ x≠-2,5$
2. Так как $x≠-2,5 ⇒ y≠-2/5$, следовательно точки $(-2,5; -2/5)$ на графике функции не существует
3. Прямая $y=kx$ будет иметь с графиком функции ровно одну общую точку в том случае, когда пройдет через точку с координатой $(-2,5; -2/5)$. Определим коэффициент $k$ линейной функции путем подстановки точки в уравнение прямой:
$k·(-2,5)=-2/5 ⇒ k=4/25=0,16$
4. Построим график:
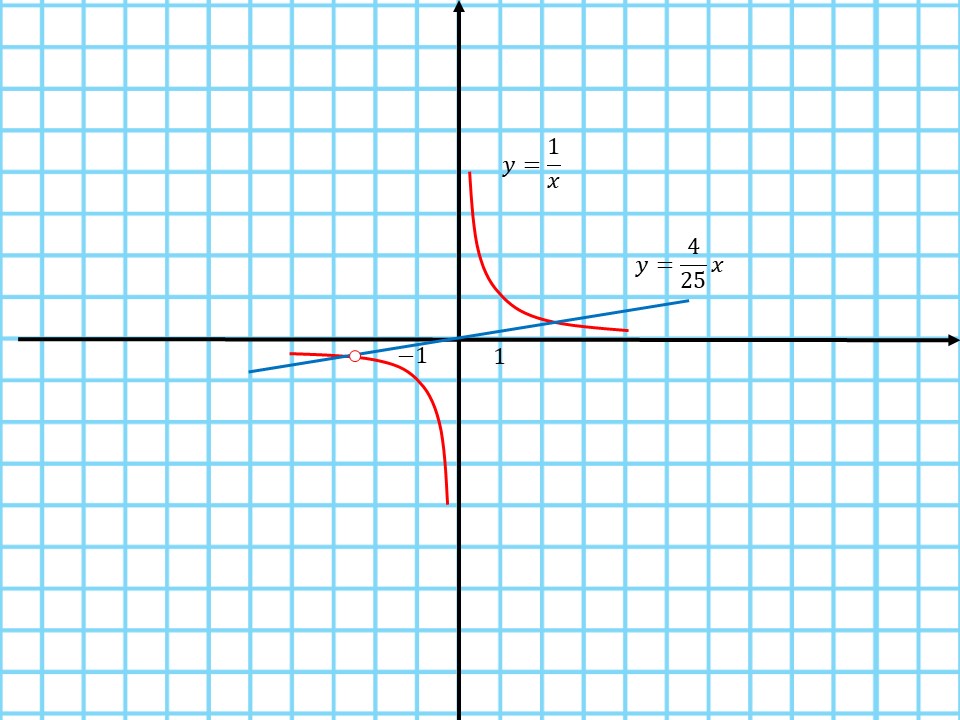
Задача 8
Постройте график функции $y={(x^2+1)(x-1)}/{1-x}$ и определите, при каких значениях $k$ прямая $y=kx$ имеет с графиком функции ровно одну общую точку. В ответ запишите наибольшее такое значение.
Решение
1. Ограничение: $1-x≠0 ⇒ x≠1$
2. Преобразуем выражение:
$y={(x^2+1)(x-1)}/{1-x}={(x^2+1)(x-1)}/{-(x-1)}=-(x^2+1)=-x^2-1$
3. Поскольку парабола и прямая имеют одну общую точку, система уравнений имеет 1 решение:
$\{{\table {y=-x^2-1}; {y=kx};} ⇔ -x^2-1=kx ⇔ x^2+kx+1=0$
Чтобы система имела единственное решение, данное квадратное уравнение должно иметь единственный корень, то есть при $D=0$:
$D=k^2-4 ⇔ k^2-4=0 ⇔ k=±2$
Прямые $y=-2x$ и $y=2x$ имеют с графиком одну общую точку.
4. Обратим внимание на то, что если $ x≠1 ⇒ y≠-2$, то есть в точке $(1; -2)$ функция не существует, а значит прямая, проходящая через нее, не имеет с графиком общих точек. Найдем коэффициент $k$, подставляя данную точку в уравнение прямой $y=kx$:
$-2=k·1 ⇒ k=-2 ⇒ y=-2x$ имеет с графиком одну общую точку. Прямые из пунктов 3 и 4 совпали (такое иногда случается, все равно нужно проверять выколотую точку отдельно)
5. Таким образом, при $k=-2$ и $k=2$ прямая $y=kx$ имеет с графиком функции одну общую точку. Наибольшее значение: $k=2$.
6. Построим графики:
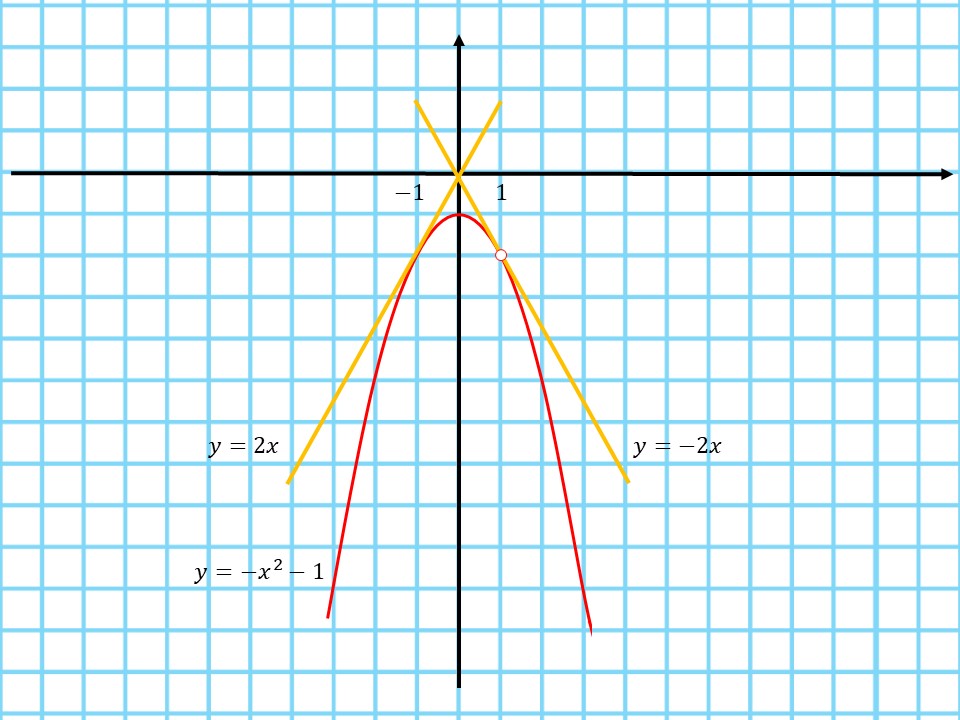
Задача 9
Постройте график функции $y={x^5+x^4}/{x^3+x^2}-3$ и определите, при каких значениях $a$ прямая $y=a$ имеет с графиком функции ровно одну общую точку.
Решение
1. Ограничение: $x^3+x^2≠0 ⇒ x≠-1; x≠0$
2. Преобразуем выражение:
$y={x^5+x^4}/{x^3+x^2}-3={x^2(x^3+x^2)}/{x^3+x^2}-3=x^2-3$
3. Построим график функции $y=x^2-3$
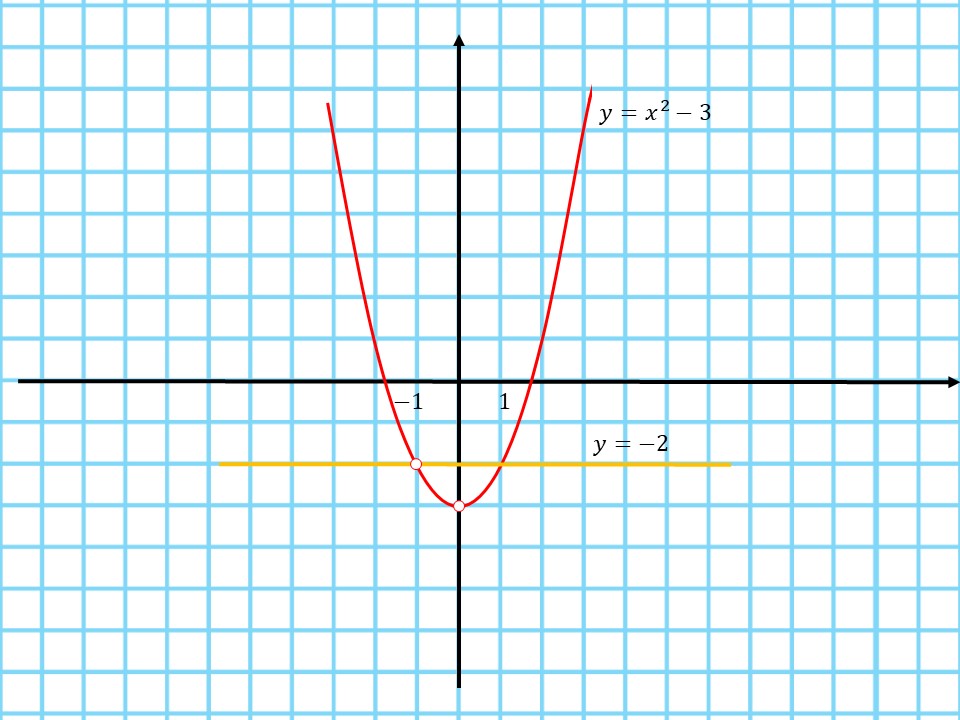
4. Выколем на графике точки, в которых функция не существует:
Если $x≠-1 ⇒ y≠-2$
Если $x≠0 ⇒ y≠-3$
5. По графику видно, что при $a=-2$ прямая $y=a$ имеет с графиком функции ровно одну общую точку.
Задача 10
Постройте график функции $y={x^4+x^3}/{x^2+x}+2$ и определите, при каких значениях $a$ прямая $y=a$ имеет с графиком функции ровно одну общую точку.
Решение
1. Ограничение: $x^2+x≠0 ⇒ x≠-1; x≠0$
2. Преобразуем выражение:
$y={x^4+x^3}/{x^2+x}+2={x^2(x^2+x)}/{x^2+x}+2=x^2+2$
3. Построим график функции $y=x^2+2$
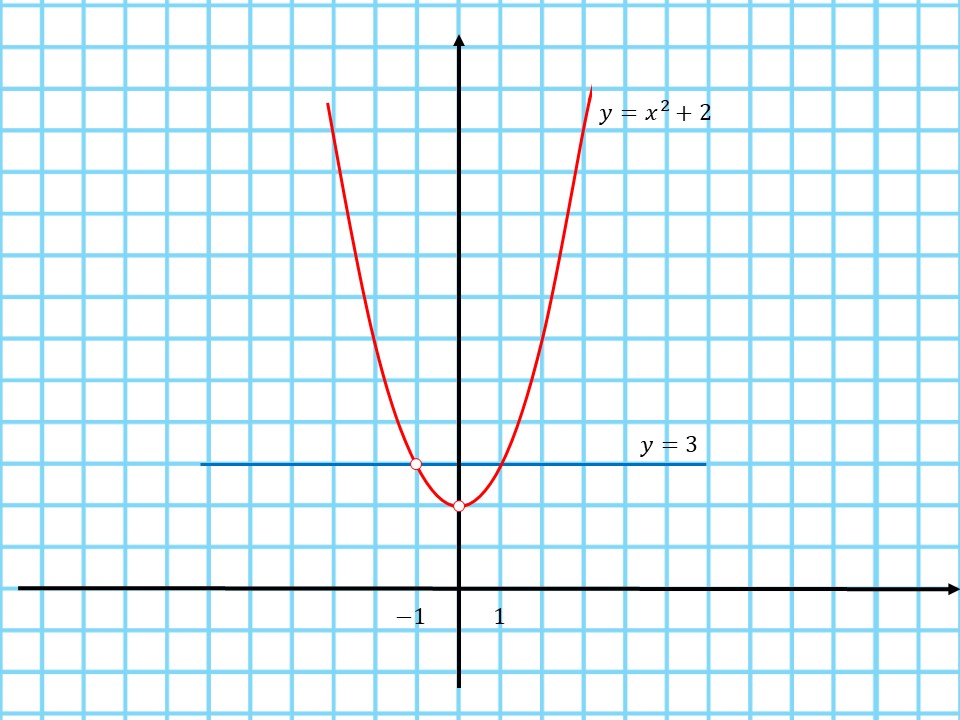
4. Выколем на графике точки, в которых функция не существует:
Если $x≠-1 ⇒ y≠3$
Если $x≠0 ⇒ y≠2$
5. По графику видно, что при $a=3$ прямая $y=a$ имеет с графиком функции ровно одну общую точку.
Задача 11
Постройте график функции $y={x^4-5x^2+4}/{(x-1)(x-2)}$ и определите, при каких значениях $a$ прямая $y=a$ имеет с графиком функции ровно одну общую точку. В ответ запишите наибольшее такое значение.
Решение
1. Разложим числитель на множители:
Пусть $x^2=t$, тогда числитель принимает вид: $t^2-5t+4=0 ⇒ t_1=1, t_2=4 ⇒ (t-1)(t-4)$
Обратная замена: $(t-1)(t-4)=(x^2-1)(x^2-4)=(x-1)(x+1)(x-2)(x+2)$
2. Сократим выражение:
$y={(x-1)(x+1)(x-2)(x+2)}/{(x-1)(x-2)}=(x+1)(x+2)=x^2+3x+2$
3. Построим график функции:
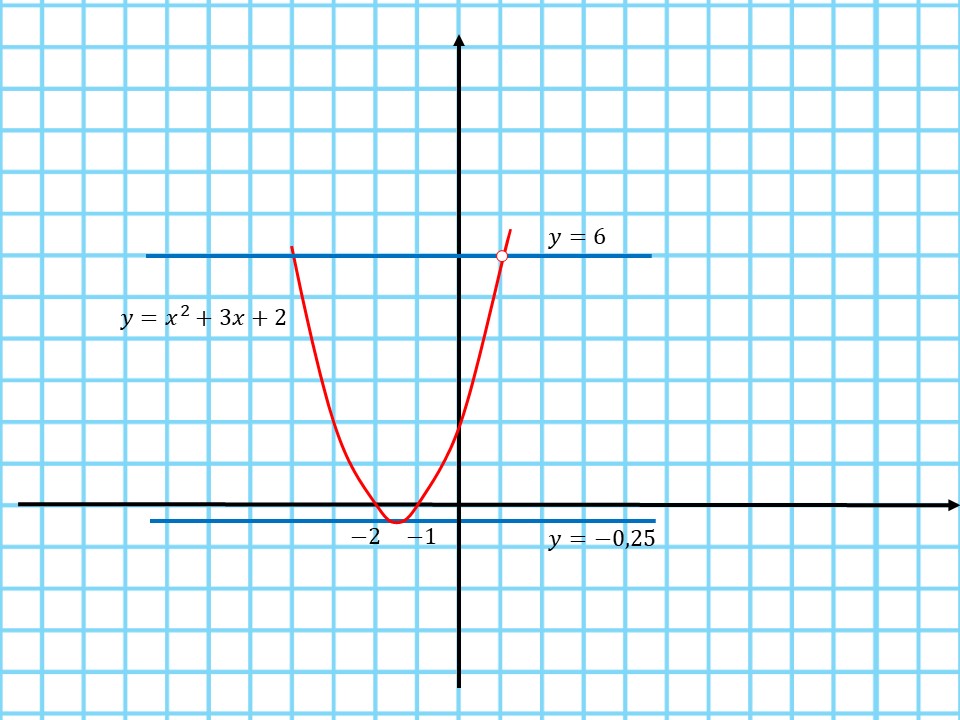
4. Определим, при каких значениях $a$ прямая $y=a$ имеет с графиком функции ровно одну общую точку:
● Это происходит в вершине параболы при $a=-0,25$
● В точках, в которых функция не существует, то есть $(x-1)(x-2)≠0 ⇒ x≠1, x≠2$
Если $x≠1 ⇒ y≠6 ⇒ a=6$
Если $x≠2 ⇒ y≠12 ⇒ a=12$
Таким образом, при $a=-0,25; a=6; a=12$ прямая $y=a$ имеет с графиком функции ровно одну общую точку.
В ответ необходимо записать наибольшее значение $a$, то есть $12$.
Задача 12
Постройте график функции $y=x^2-|4x|$ и определите, при каких значениях $p$ прямая $y=p$ имеет с графиком функции ровно три общие точки.
1. $p=0$
2. $p=-4$
3. $p∈(-4; 0)$
4. $p∈(0; +∞)$
Решение
Подмодульное выражение равно нулю при $x=0$. Раскроем знак модуля:
$\{{\table {x^2-4x, \text ' при ' x≥0}; {x^2+4x, \text ' при ' x<0}$
График функции изображен на рисунке:
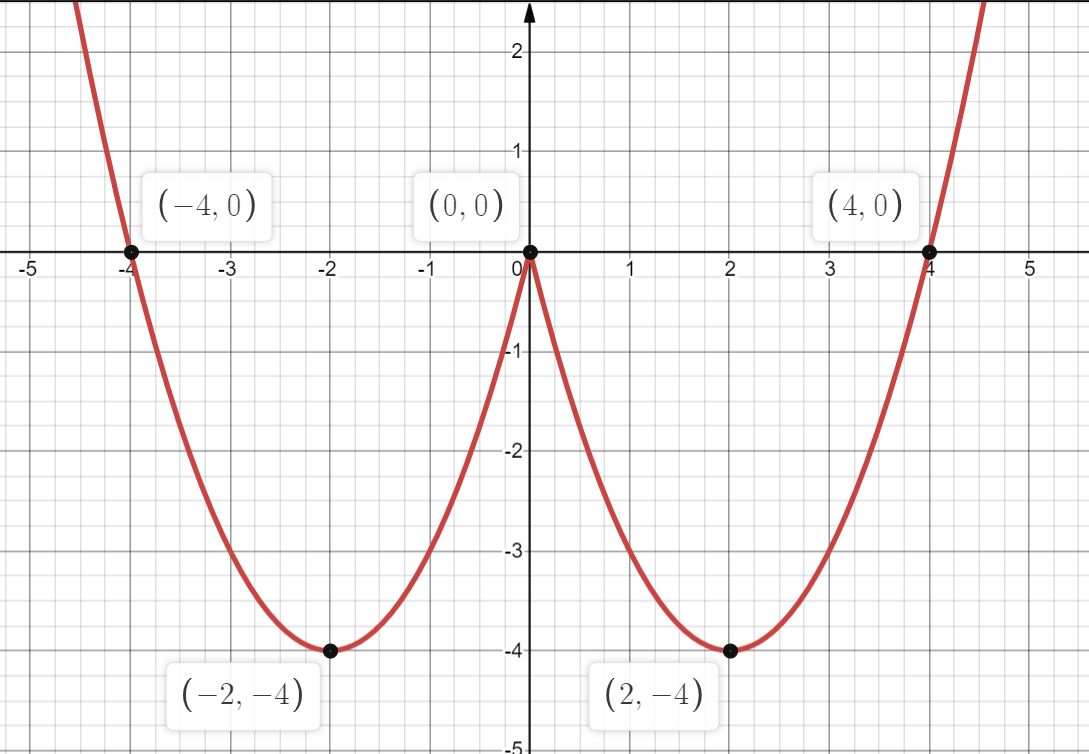
При $p=0$ прямая $y=p$ имеет с графиком функции ровно три общие точки.
Задача 13
Постройте график функции $y={x^4-17x^2+16}/{(x-4)(x-1)}$ и определите, при каких значениях $a$ прямая $y=a$ имеет с графиком функции ровно одну общую точку. В ответ запишите наибольшее такое значение.
Решение
1. Разложим числитель на множители:
Пусть $x^2=t$, тогда числитель принимает вид: $t^2-17t+16=0 ⇒ t_1=1, t_2=16 ⇒ (t-1)(t-16)$
Обратная замена: $(t-1)(t-16)=(x^2-1)(x^2-16)=(x-1)(x+1)(x-4)(x+4)$
2. Сократим выражение:
$y={(x-1)(x+1)(x-4)(x+4)}/{(x-4)(x-1)}=(x+1)(x+4)=x^2+5x+4$
3. Построим график функции:
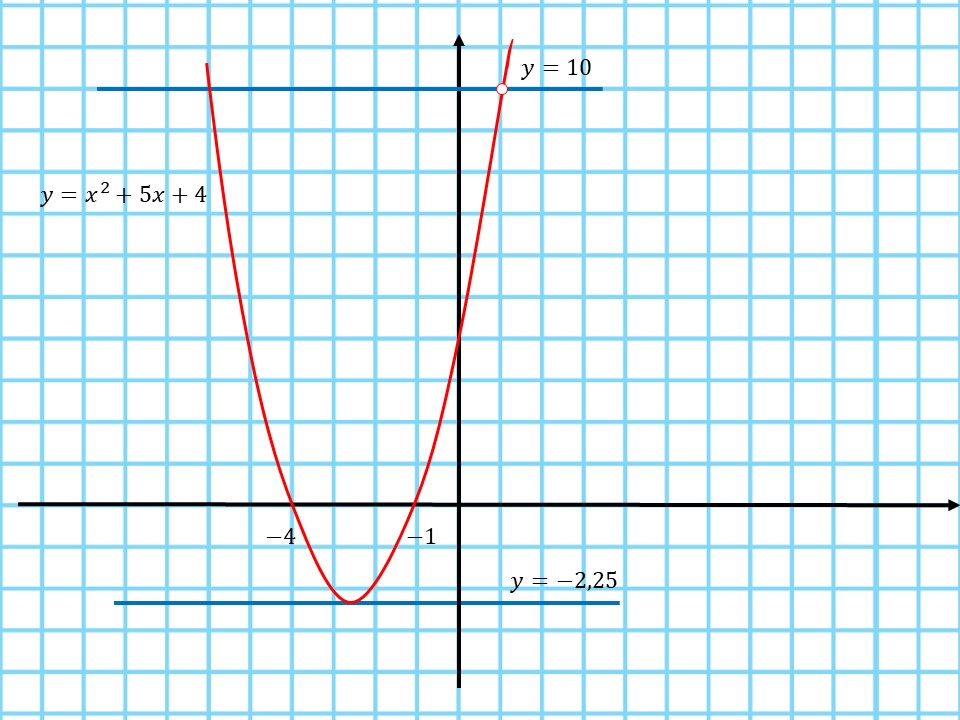
4. Определим, при каких значениях $a$ прямая $y=a$ имеет с графиком функции ровно одну общую точку:
● Это происходит в вершине параболы при $a=-2,25$
● В точках, в которых функция не существует, то есть $(x-4)(x-1)≠0 ⇒ x≠1, x≠4$
Если $x≠1 ⇒ y≠10 ⇒ a=10$
Если $x≠4 ⇒ y≠40 ⇒ a=40$
Таким образом, при $a=-2,25; a=10; a=40$ прямая $y=a$ имеет с графиком функции ровно одну общую точку.
В ответ необходимо записать наибольшее значение $a$, то есть $40$.
Задача 14
При каком наибольшем значении $a$ прямая $y=ax-2$ имеет с графиком функции $y=x^2-1$ ровно одну общую точку (касается)? Построить график квадратичной функции и касательные к нему.
Решение
Функция $y=ax-2$ и $y=x^2-1$ имеют одну общую точку в том случае, когда система уравнений имеет единственное решение:
$\{{\table {y=ax-2}; {y=x^2-1}$ $⇔$ $x^2-1=ax-2$ $⇔$ $x^2-ax+1=0$
Уравнение имеет единственный корень при $D=0$:
$D=a^2-4 ⇔ a^2-4=0 ⇔ a=±2$
Таким образом, прямые $y=-2x-2$ и $y=2x-2$ являются касательными к графику функции $y=x^2-1$.
Построим графики:
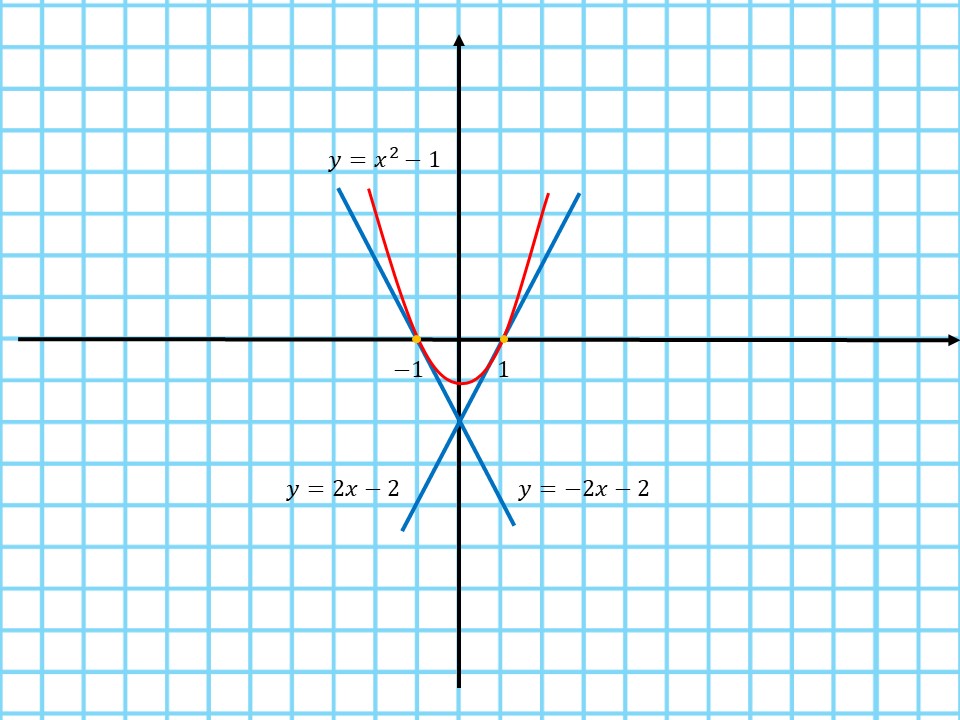
Наибольшее значение: $a=2$.
Задача 15
Постройте график функции $y=x^2-2|x-1|-2x+4$ и определите, при каких значениях $p$ прямая $y=p$ имеет с графиком функции ровно три общие точки.
Решение
Подмодульное выражение равно нулю при $x=1$. Раскроем знак модуля:
$\{{\table {x^2-2(x-1)-2x+4, \text ' при ' x≥1}; {x^2+2(x-1)-2x+4, \text ' при ' x<1}$ $⇔$ $\{{\table {x^2-2x+2-2x+4, \text ' при ' x≥1}; {x^2+2x-2-2x+4, \text ' при ' x<1}$ $⇔$ $\{{\table {x^2-4x+6, \text ' при ' x≥1}; {x^2+2, \text ' при ' x<1}$
График функции изображен на рисунке:

При $p=3$ прямая $y=p$ имеет с графиком функции ровно три общие точки.
Задача 16
Постройте график функции $y=|x|(x+1)-3x$ и определите, при каких значениях $p$ прямая $y=p$ имеет с графиком функции ровно две общие точки.
1. $p=-1$ и $p=4$
2. $p=-4$
3. $p∈(-1; 4)∪(4; +∞)$
4. $p∈(-1; 4)$
Решение
Подмодульное выражение равно нулю при $x=0$. Раскроем знак модуля:
$\{{\table {x(x+1)-3x, \text ' при ' x≥0}; {-x(x+1)-3x, \text ' при ' x<0}$ $⇔$ $\{{\table {x^2+x-3x, \text ' при ' x≥0}; {-x^2-x-3x, \text ' при ' x<0}$ $⇔$ $\{{\table {x^2-2x, \text ' при ' x≥0}; {-x^2-4x, \text ' при ' x<0}$
График функции изображен на рисунке:
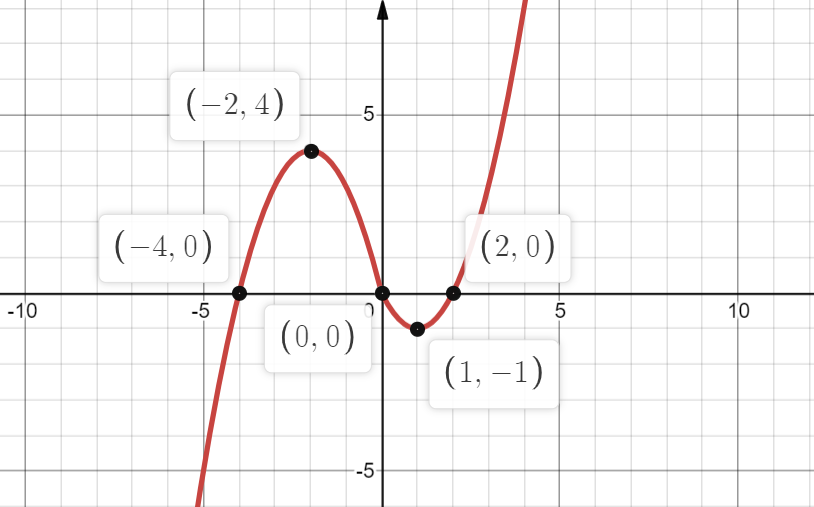
При $p=-1$ и $p=4$ прямая $y=p$ имеет с графиком функции ровно две общие точки.
Задача 17
Постройте график функции $y=|x|(x+2)-4x$ и определите, при каких значениях $p$ прямая $y=p$ имеет с графиком функции ровно три общие точки.
1. $p=-1$
2. $p=-9$
3. $p∈(-1; 0)∪(9; +∞)$
4. $p∈(-1; 9)$
Решение
Подмодульное выражение равно нулю при $x=0$. Раскроем знак модуля:
$\{{\table {x(x+2)-4x, \text ' при ' x≥0}; {-x(x+2)-4x, \text ' при ' x<0}$ $⇔$ $\{{\table {x^2+2x-4x, \text ' при ' x≥0}; {-x^2-2x-4x, \text ' при ' x<0}$ $⇔$ $\{{\table {x^2-2x, \text ' при ' x≥0}; {-x^2-6x, \text ' при ' x<0}$
График функции изображен на рисунке:

При $p∈(-1; 9)$ прямая $y=p$ имеет с графиком функции ровно три общие точки.
Задача 18
Постройте график функции $y=|x|(x-1)-5x$ и определите, при каких значениях $p$ прямая $y=p$ имеет с графиком функции ровно две общие точки.
1. $p∈(-∞; -9)∪(4; +∞)$
2. $p=-9$ и $p=4$
3. $p∈(-9; 4)$
4. $p=4$
Решение
Подмодульное выражение равно нулю при $x=0$. Раскроем знак модуля:
$\{{\table {x(x-1)-5x, \text ' при ' x≥0}; {-x(x-1)-5x, \text ' при ' x<0}$ $⇔$ $\{{\table {x^2-x-5x, \text ' при ' x≥0}; {-x^2+x-5x, \text ' при ' x<0}$ $⇔$ $\{{\table {x^2-6x, \text ' при ' x≥0}; {-x^2-4x, \text ' при ' x<0}$
График функции изображен на рисунке:

При $p=-9$ и $p=4$ прямая $y=p$ имеет с графиком функции ровно две общие точки.
Задача 19
Постройте график функции $y=x^2-3|x|+x$ и определите, при каких значениях $p$ прямая $y=p$ имеет с графиком функции ровно три общие точки. В ответ запишите наибольшее такое значение.
Решение
Подмодульное выражение равно нулю при $x=0$. Раскроем знак модуля:
$\{{\table {x^2-3x+x, \text ' при ' x≥0}; {x^2+3x+x, \text ' при ' x<0}$ $⇔$ $\{{\table {x^2-2x, \text ' при ' x≥0}; {x^2+4x, \text ' при ' x<0}$
График функции изображен на рисунке:
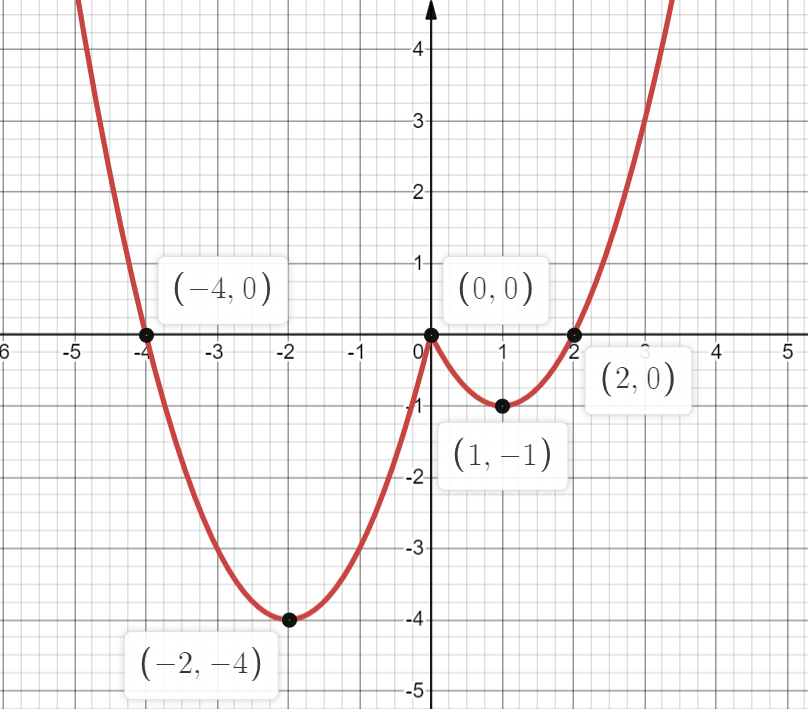
При $p=-1$ и $p=0$ прямая $y=p$ имеет с графиком функции ровно три общие точки. Наибольшее такое значение: $p=0$.
Задача 20
Первая прямая проходит через точки с координатами $(-5; 4)$ и $(-1; -4)$, вторая - через точки $(-4; -1)$ и $(2; 5)$. Найдите координату точки пересечения данных прямых. В ответ запишите значение переменной $x$.
Решение
Воспользуемся формулой нахождения уравнения прямой, проходящей через 2 точки, где $(x_1; y_1)$ и $(x_2; y_2)$ - координаты точки, через которые проходит прямая:
${x-x_1}/{x_2-x_1}={y-y_1}/{y_2-y_1}$
1. Первая прямая проходит через точки $(-5; 4)$ и $(-1; -4)$, подставим в формулу:
${x-(-5)}/{-1-(-5)}={y-4}/{-4-4} ⇔ {x+5}/{4}={y-4}/{-8} ⇔ y=-2x-6$ - уравнение 1 прямой
2. Вторая прямая проходит через точки $(-4; -1)$ и $(2; 5)$, подставим в формулу:
${x-(-4)}/{2-(-4)}={y-(-1)}/{5-(-1)} ⇔ {x+4}/{6}={y+1}/{6} ⇔ y=x+3$ - уравнение 2 прямой
3. Чтобы найти точку пересечения прямых, необходимо найти решение системы:
$\{{\table {y=-2x-6}; {y=x+3}$ $⇔$ $\{{\table {x=-3}; {y=0}$
4. В ответ необходимо записать значение переменной $x$, то есть $-3$.
Рекомендуемые курсы подготовки

- Разберешься в разных типах функций
- Сможешь быстро решать задания №11 ОГЭ и заберешь свой балл за него на экзамене
- Получишь крутую базу для задания №22 из письменной части ОГЭ
- Поймешь, что графики функций не так страшны, как казалось раньше
на бесплатном курсе Турбо ЕГЭ

