Задание 23. Геометрическая задача на вычисление. ОГЭ 2026 по математике
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 11, а одна из диагоналей равна 44. Найдите углы ромба. В ответ запишите больший угол ромба
Решение
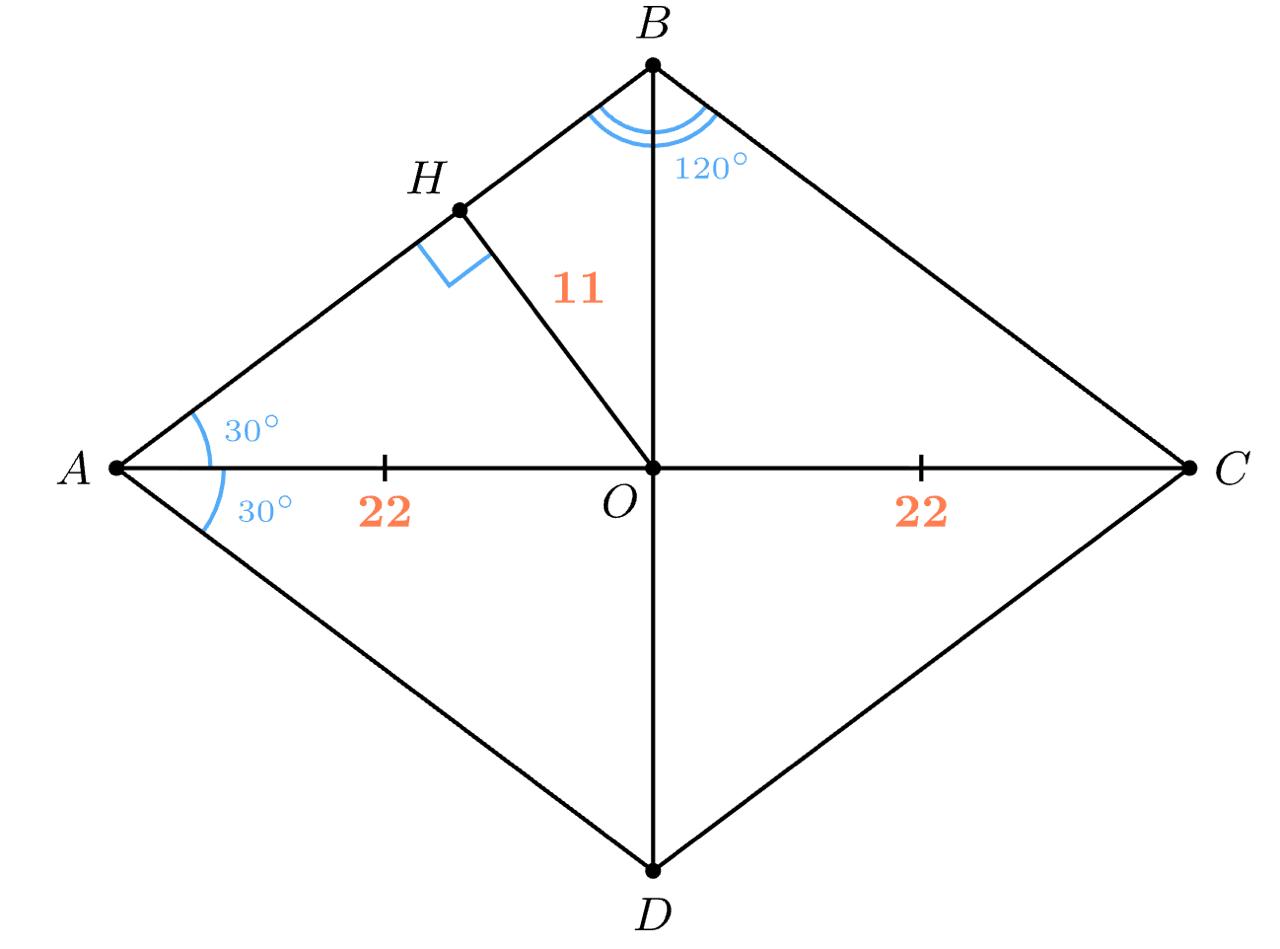
Пусть дан ромб ABCD, а его диагонали AC = 44 и BD пересекаются в точке O. Опустим из точки O перпендикуляр OH на сторону AB. По условию OH = 11.
Ромб является параллелограммом, поэтому его диагонали точкой пересечения делятся пополам, следовательно, $AO =OC = {1}/{2}⋅AC = {1}/{2}⋅44 = 22.$
Треугольник AHO — прямоугольный, так как OH ⊥ AB. Заметим, что в нём: ${OH}/{AO}={11}/{22}={1}/{2}$
Если в прямоугольном треугольнике катет равен половине гипотенузы, то он лежит против угла в 30°, следовательно, ∠HAO = 30° .
Диагонали ромба являются биссектрисами его углов, поэтому AC — биссектриса ∠BAD, следовательно, ∠BAD = 2∠HAO =2 ⋅30° =60°.
Противоположные углы ромба равны, поэтому ∠BCD = ∠BAD =60°.
Сумма углов ромба 360°, найдем $∠B=∠D={360°-60°-60°}/{2}=120°$
Задача 2
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите длину отрезка CM, если AB = 10, CD = 25, AC = 56.
Решение
Обозначим искомую сторону МС как х, тогда:
АМ = АС – МС = 56 – х
ΔАМВ ∼ ΔDCM подобны по двум равным углам: ∠АМВ = ∠DMC, как вертикальные, ∠MAB = ∠MCD, как накрест лежащие при параллельных прямых АВ||DC и секущей АС.
Соответствующие стороны треугольников пропорциональны:
${AB}/{CD}={AM}/{MC}$
${10}/{25}={56-x}/{x}$ (cокращаем дробь слева на 2 и перемножаем крест на крест)
$2·x = 5·(56 – x)$
$2x = 280 – 5x$
$2x + 5x = 280$
$7x = 280$
$x = {280}/{7} = 40$
Задача 3
Высота AH ромба ABCD делит сторону CD на отрезки DH =21 и CH = 8. Найдите высоту ромба.
Решение
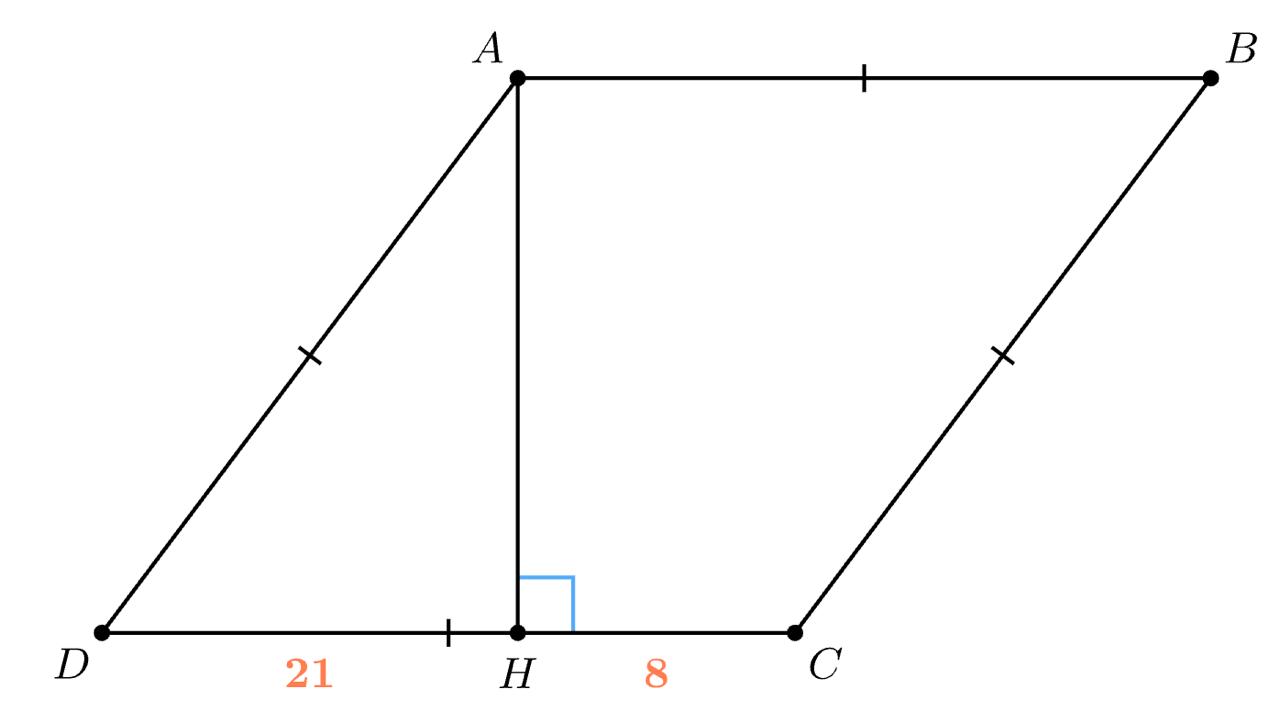
Найдём DC : DC = DH + HC =21 +8 = 29.
По условию ABCD — ромб, поэтому AB = BC = CD = AD =29.
Рассмотрим треугольник AHD. Он прямоугольный, так как AH ⊥ DC, ведь AH — высота ромба по условию. Тогда по теореме Пифагора для треугольника AHD : $AD^2 = DH^2 + AH^2.$
$AH^2 = AD^2 − DH^2$
$AH^2 = 29^2 − 21^2$
$AH^2 = 841 − 441$
$AH^2 = 400$
AH = 20
Задача 4
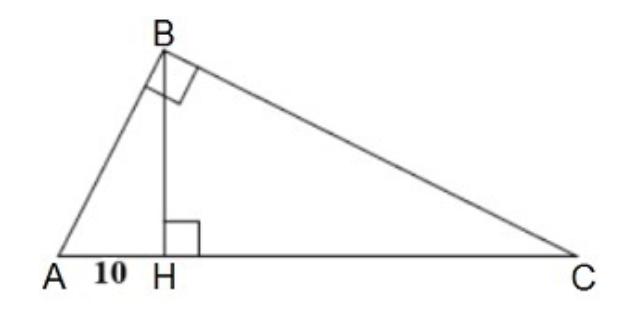
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 10, AC = 40.
Решение
Рассмотрим ΔABC и ΔABH в них ∠A общий, ∠ABC = ∠AHB как прямые углы. Значит, треугольники подобны по двум равным углам.
Запишем отношение сторон: ${AB}/{AC}={AH}/{AB}$
$AB·AB = AC·AH$
$AB^2 = 40·10 = 400$
$AB = √400 = 20$
Ответ: 20.
Задача 5
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD = 36. Ответ сократите на $√6 $
Решение
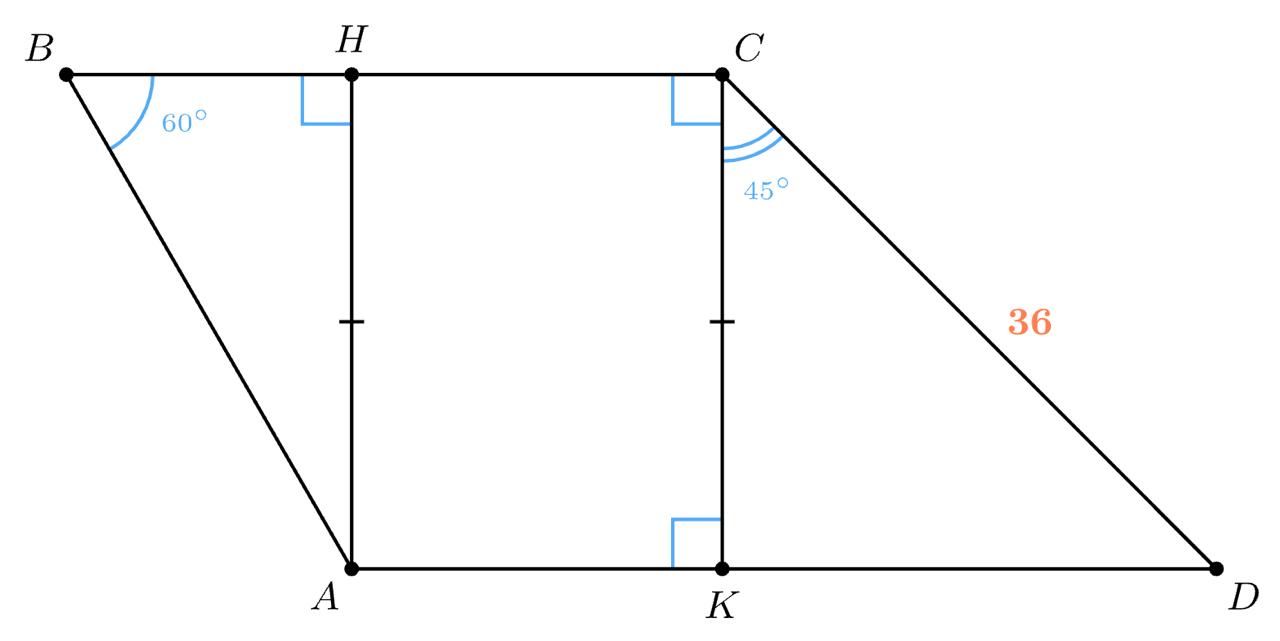
1) Проведём высоты AH и CK трапеции ABCD. Тогда $∠AHB = 90° = ∠BCK.$
Значит, $∠KCD = ∠BCD − ∠BCK = 135°− 90° = 45°.$
2) Рассмотрим треугольник CKD, в нем: ∠KCD=45°, ∠CKD=90°, так как CK - высота. Найдем $∠СDK: ∠СDK=180°-90°-45°=45°$ => треугольник CKD - равнобедренный
3) Пусть $CK=KD=x.$ Тогда по теореме Пифагора найдем CD:
$CK^2+KD^2=CD^2$
$x^2+x^2=36^2$
$2x^2=1296$
$x^2=648$
$x=√648$
$CK=KD=√648$
3) Высоты трапеции равны между собой => $CK=AH=√648$
4) Рассмотрим треугольник ABH, в нем: $∠ABH=60°$ (по условию), $∠BHA=90°$, так как AH-высота, найдем ∠BAH:
$∠BAH=180°-90°-60°=30°$
5) Напротив угла в 30° в прямоугольном треугольнике лежит катет равный половине гипотенузы => $AB=2BH$
Пусть BH=x, тогда AB=2x, по теореме Пифагора:
$AH^2+BH^2=AB^2$
$(√648)^2+x^2=(2x)^2$
$3x^2=648$
$x^2=216$
$x=√216=√{36·6}=6√6$
$AB=2x=2·6√6=12√6$
Сокращаем на $√6,$ получаем 12
Ответ: 12
Задача 6
Высота $BK$ ромба $ABCD$ делит сторону $CD$ на отрезки $CK = 12$ и $KD = 8$. Найдите высоту ромба.
Решение
Задача 7
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как $1$ : $2$ : $3$. Найдите радиус окружности, если меньшая из сторон равна $14$.
Решение
Задача 8
Отрезки $AC$ и $BD$ являются хордами окружности. Найдите длину хорды $BD$, если $AC = 24$, а расстояния от центра окружности до хорд $AC$ и $BD$ равны соответственно $35$ и $12$.
Решение
Задача 9
Окружность с центром на стороне $MN$ треугольника $MNP$ проходит через вершину $N$ и касается прямой $MP$ в точке $P$ . Найдите диаметр окружности, если $MP = 16$, $MN = 20$.
Решение
Задача 10
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна $7$.
Решение
Задача 11
Катеты прямоугольного треугольника равны $7$ и $24$. Найдите высоту, проведённую к гипотенузе.
Решение
Задача 12
Отрезки $AC$ и $BD$ являются хордами окружности. Найдите длину хорды $AC$, если $BD = 42$, а расстояния от центра окружности до хорд $AC$ и $BD$ равны соответственно $21$ и $20$.
Решение
Задача 13

На сторонах угла $MNP$ и на его биссектрисе отложены равные отрезки $MN$, $NP$ и $NA$ (см. рис.). Величина угла $MAP$ равна $142^°$. Определите величину угла $MNP$ . Ответ дайте в градусах.
Решение
Задача 14
В трапеции $ABCD$ боковые стороны $AD$ и $BC$ равны, $BK$ — высота, проведённая к большему основанию $CD$. Найдите длину отрезка $CK$, если средняя линия $MN$ трапеции равна $15$, а меньшее основание $AB$ равно $4$.
Решение
Задача 15
В трапецию, сумма длин боковых сторон которой равна $19$, вписана окружность. Найдите длину средней линии трапеции.
Решение
Задача 16
Прямая $CK$, перпендикулярная медиане $BD$ треугольника $ABC$, делит её пополам. Найдите сторону $AC$, если сторона $BC$ равна $8$.
Решение
Задача 17
Биссектрисы углов $B$ и $C$ параллелограмма $ABCD$ пересекаются в точке, лежащей на стороне $AD$. Найдите $AD$, если $CD = 14,5$.
Решение
Задача 18
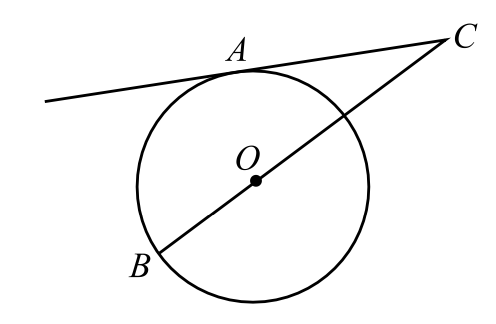
Найдите угол $ACO$, если его сторона $AC$ касается окружности с центром в точке $O$, а дуга $AB$, заключённая внутри этого угла, равна $150^°$ (см. рис.).
Решение
Задача 19
Биссектриса угла $C$ параллелограмма $ABCD$ пересекает его сторону $AD$ в точке $F$. Найдите площадь параллелограмма $ABCD$, если $FD = 9$, $AF = 2$, а $∠ADC = 150^°$
Решение
Задача 20
Углы $M$ и $N$ треугольника $MPN$ равны соответственно $72^°$ и $78^°$. Найдите $MN$, если радиус окружности, описанной около треугольника $MPN$, равен $6$
Решение
Рекомендуемые курсы подготовки

- Разберешься в разных типах функций
- Сможешь быстро решать задания №11 ОГЭ и заберешь свой балл за него на экзамене
- Получишь крутую базу для задания №22 из письменной части ОГЭ
- Поймешь, что графики функций не так страшны, как казалось раньше
на бесплатном курсе Турбо ЕГЭ

