Задание 1. Анализ информационных моделей. Графы.. ЕГЭ 2026 по информатике
Средний процент выполнения: 89%
Ответом к заданию 1 по информатике может быть цифра (число) или слово.
Алгоритм решения задания 1:
- Определи, какая модель дана в условии (схема, карта, таблица, график или формула).
- Прочитай, что требуется найти: значение, зависимость, элемент модели или вывод по модели.
- Выдели в модели ключевые элементы (подписи, оси/шкалы, обозначения, связи, строки/столбцы).
- Считай нужные данные из модели строго по обозначениям и шкалам.
- Если требуется преобразование, выполни его (перевод по шкале, вычисление по формуле, сравнение значений).
- Проверь ответ обратной подстановкой в модель: соответствует ли он исходным данным.
- Запиши ответ в требуемом формате (число/последовательность символов).
Подпишись на суперполезные материалы

Задачи для практики
Задача 1
Задание: Хронограф
Цель: научиться осознанно управлять своим временем и найти скрытые резервы для подготовки к ЕГЭ.
Что нужно сделать:
-
В течение 7 дней вести хронограф — подробный учёт того, как вы тратите время в течение дня.
- Можно использовать таблицу, приложение для тайм-трекинга или просто блокнот.
- Фиксируйте каждый блок времени (например, с точностью до 30 минут или часа).
- Отмечайте: учёба, ЕГЭ-подготовка, сон, дорога, еда, соцсети, игры, отдых, домашние дела и т.д.
-
В конце недели проанализируйте данные:
- Сколько времени уходит на разные виды активности?
- Где вы теряете время впустую?
- Сколько реально времени уходит на подготовку к ЕГЭ?
- Где можно найти дополнительные 1–2 часа в день для учёбы?
В качестве ответа на это задание просто отправь 1, и решение будет зачтено :)
Решение
Если не знаешь, с чего начать, или нужна помощь в анализе результатов - напиши в лс группы, я обязательно помогу тебе со всем разобраться.
Задача 2
Вопрос Каким оператором в Python выполняется возведение в степень?
Решение
Решение: В Python возведение в степень выполняется оператором **. Например, 2 ** 3 означает «2 в кубе» и даёт результат 8. Остальные варианты: ^ — это побитовое XOR, * — обычное умножение, // — целочисленное деление.
Задача 3
Будь внимательнее. Что выведет код?
print("2" + "3")
Решение
Решение: Здесь важно заметить, что внутри кавычек — это строки, а не числа. Оператор + в случае строк выполняет конкатенацию (склеивание), а не сложение. Поэтому результат будет "23". На экран выведется строка 23, а не число 5. Многие ученики ошибочно думают, что произойдёт именно сложение.
Задача 4
Какая функция в Python используется для ввода данных от пользователя? Скобки, которые идут вместе с этой функцией тоже надо записать в ответ
Решение
Решение: Функция input() предназначена для того, чтобы пользователь мог ввести данные с клавиатуры. По умолчанию input() всегда возвращает строку, поэтому если нужны числа, результат нужно преобразовать с помощью int() или float(). Остальные варианты выполняют другие задачи: print() выводит информацию на экран, int() преобразует к целому числу, str() — к строке.
Задача 5
Вопрос. Что выведет следующий код?
print(2 + 3 * 4)
Решение
Решение: В Python действует стандартный порядок арифметических операций: сначала умножение и деление, затем сложение и вычитание. Сначала считается 3 * 4 = 12, а затем выполняется сложение 2 + 12 = 14. Поэтому правильный ответ: 14.
Задача 6
Вопрос Что вернёт выражение 7 % 3 ?
Решение
Решение: Оператор % возвращает остаток от деления. При делении 7 на 3 получается 2 целых и остаток 1. Значит, результат выражения 7 % 3 равен 1. Поэтому правильный ответ: 1.
Задача 7
Вопрос Какой тип данных получится в результате выражения 5 / 2 ? Скобки писать не нужно, просто слово на английском
Решение
Решение: В Python оператор / всегда выполняет деление с результатом в виде числа с плавающей точкой (float). Даже если результат «красивый» (например, 4 / 2 = 2.0), всё равно возвращается float, а не int. Поэтому правильный ответ: float.
Задача 8
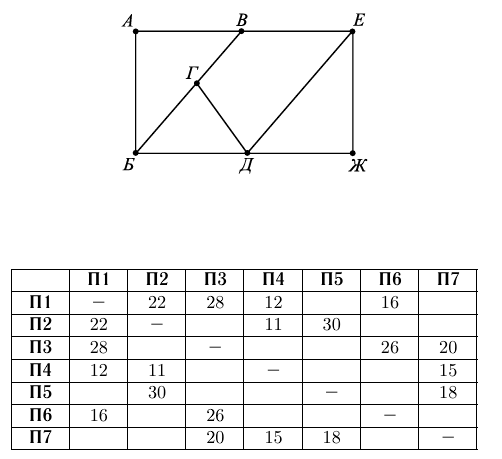
На рисунке изображена схема дорог в виде графа, в таблице содержатся сведения о протяжённости этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите сумму протяжённостей дорог между пунктом А и пунктом Б и между пунктом Е и пунктом Ж
Решение
Поселок Д - единственный имеет 4 дороги, его номер - 1. Поселок А - единственный имеет 2 дороги, которые ведут в пункты с 3 дорогами, его номер - 5. Поселок Ж - оставшийся с двумя дорогами, его номер - 6. Отсюда делаем вывод, что поселок Е - 3, значит В - 7, значит Б - 2
Задача 9
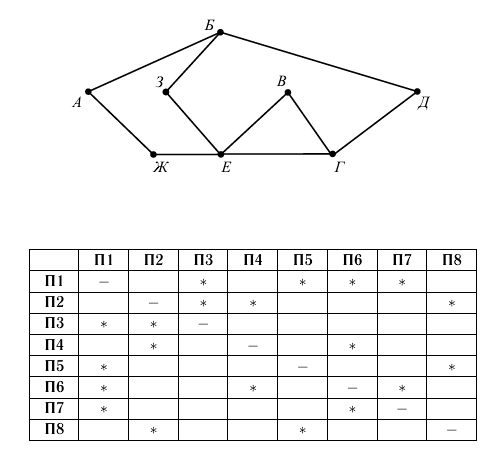
На рисунке изображена схема дорог в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Отсутствие звёздочки означает, что такой дороги нет. Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначения ми на графе. Выпишите последовательно, без пробелов и
знаков препинания, указанные на графе буквенные обозначения пунктов
от П4доП7:сначала букву, соответствующую П4, затем букву, соответствующую П5, и т.д.
Решение
Поселок е - единственный имеет 4 дороги, его номер - 1. Номер поселка Г соответственно - 6, тогда поселок В - 7, так как соединен и с Е и с Г. Теперь необходимо последовательно пройтись по графу, например, номер поселка Д - 4. Номер поселка Б - 2
Задача 10

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите длину кратчайшего маршрута между населёнными пунктами E и C на схеме.
Решение
Поселок Б - единственный имеет 1 дорогу, его номер - 7. Поселок А - единственный имеет 6 дорог, его номер - 4. Поселок С - единственный имеет 3 дороги, его номер - 2. Значит пункт D и B это 1 или 5. Теперь расставим протяженность дорог от каждого пункта. Видно, что минимальный путь это E-A-C = 6 + 10
Задача 11
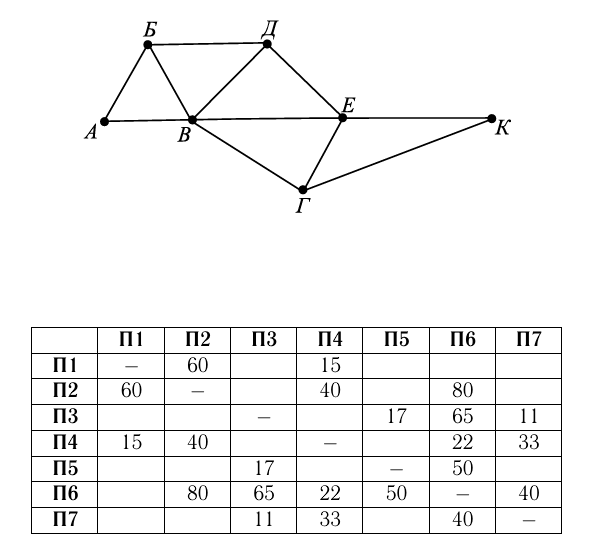
На рисунке изображена схема дорог Н-ского района в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Д. В ответе запишите целое число.
Решение
Поселок В - единственный имеет 5 дорог, его номер - 6. Теперь легко найти Б и Д, это пункты 3 и 7
Задача 12

На рисунке изображена схема дорог Н-ского района в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите, какова сумма протяжённостей дорог из пункта F в пункт B и из пункта Е в пункт D.
Решение
Уникальный пункт это С, его номер - 5. Значит Пункты D и B это либо 1, либо 7. Теперь необходимо посмотреть длину пути до пункта с длиной 4
Задача 13

На рисунке изображена схема дорог Н-ского района в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначения ми на графе. Определите длину дороги из пункта Е в пункт К.
В ответе запишите целое число.
Решение
Поселок Е - единственный имеет 4 дороги, его номер - 4. Поселок Г - единственный имеет 3 дороги, его номер - 2. Отсюда делаем вывод, что пункт К имеет номер - 1, так как соединен с Е и Г
Задача 14
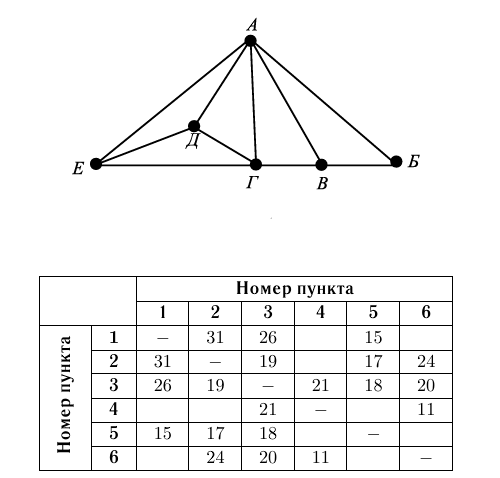
На рисунке изображена схема дорог в виде графа, в таблице содержатся сведения о протяжённости этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите, какова длина дороги из пункта Г в пункт В. В ответе запишите целое число.
Решение
Поселок г - единственный имеет 4 дороги, его номер - 2. Поселок Б - единственный имеет 2 дороги, его номер - 4. Значит поселок В - 6
Задача 15
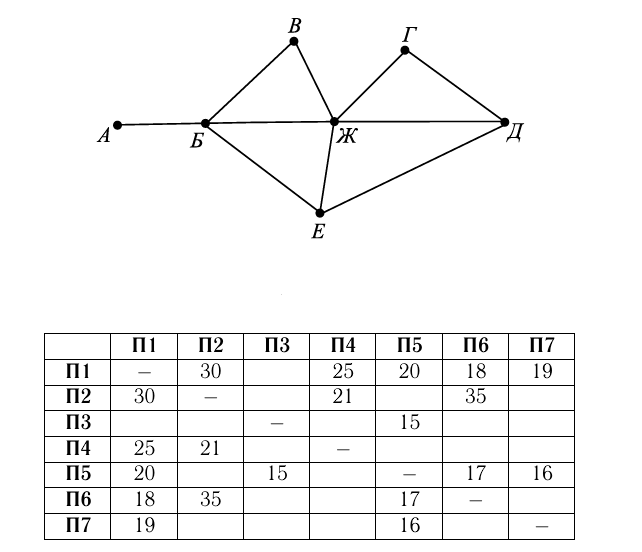
На рисунке изображена схема дорог Н-ского района в виде графа,в таблице содержатся сведения о длинах этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Д в пункт Е. В ответе запишите целое число.
Решение
Поселок Б - единственный имеет 4 дороги, его номер - 5. Номер поселка Е соответственно - 6, тогда поселок Д - 2. Длина между ними 35
Задача 16
На рисунке изображена схема дорог между поселками в виде графа, а в таблице содержится информация о протяженности дорог между поселками.
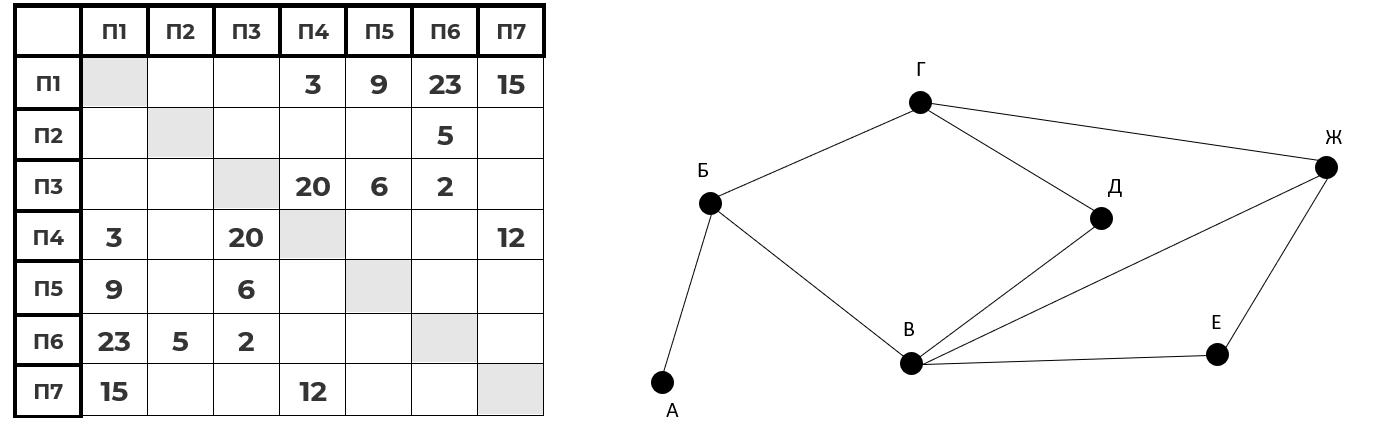
Так как и таблицу, и схему составляли независимо друг от друга, то буквенные обозначения поселков на схеме никак не связаны с их нумерацией в таблице. Определите кратчайший путь из пункта А в пункт Ж. В ответе запишите целое число, означающее протяжённость пути.
Решение
Для начала нужно посчитать количество рёбер в таблице и на графике
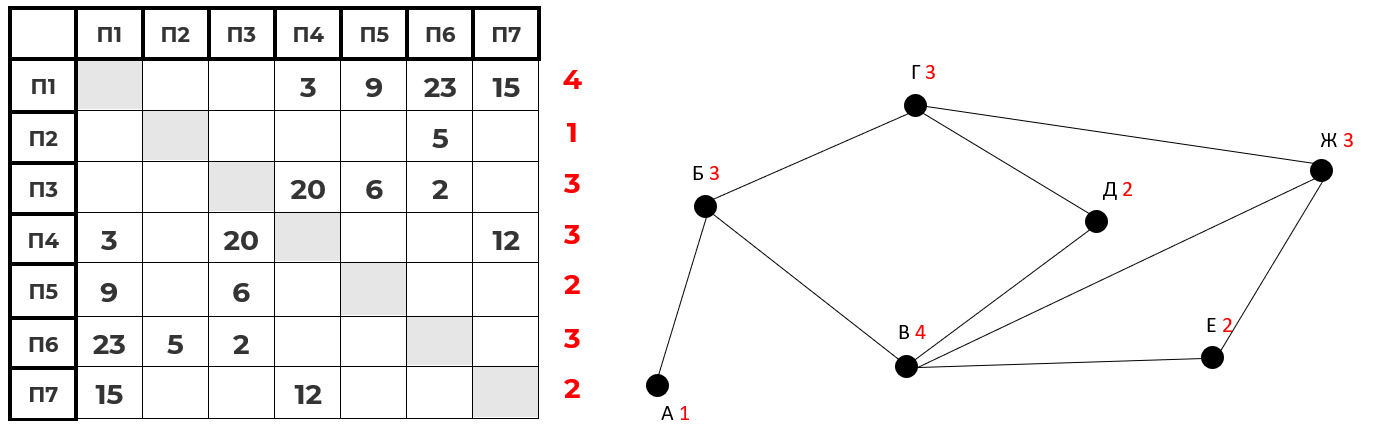
После этого, нужно соотнести названия пунктов с названиями вершин и в таблице обозначить все вершины. Пункты А и В являются уникальными. С ними соединён пункт Б. Эти три пункта определить проще всего.
Далее можно найти пункт Г, а после него пункт Д и потом оставшиеся.
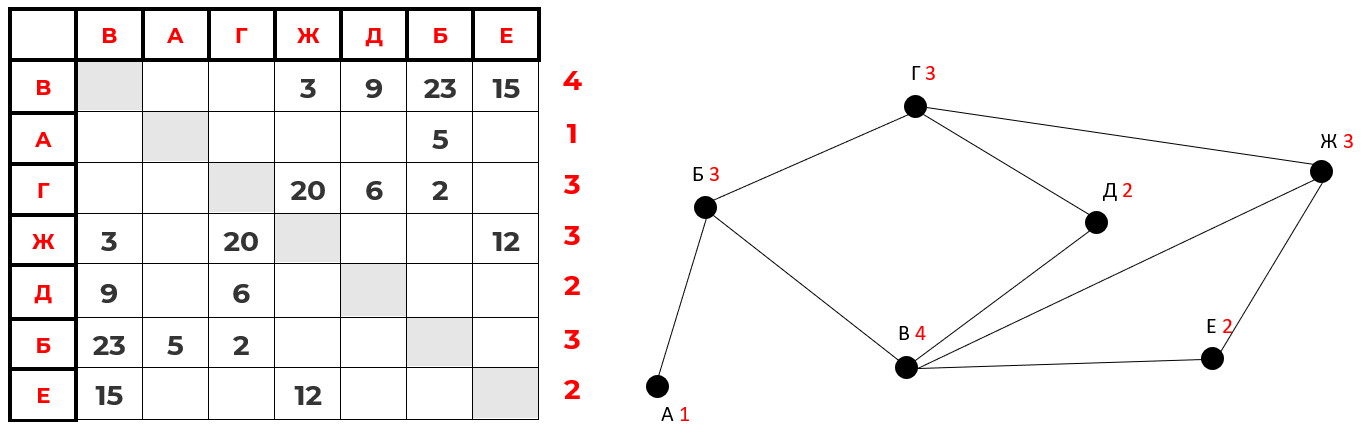
На графе обозначьте вес рёбер. После этого найдите кратчайшее расстояние от пункта А до пункта Ж.
Учитывайте, что до пункта В можно добраться через пункт Г (маршрут А-Б-Г-Д-В-Ж).
Задача 17
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
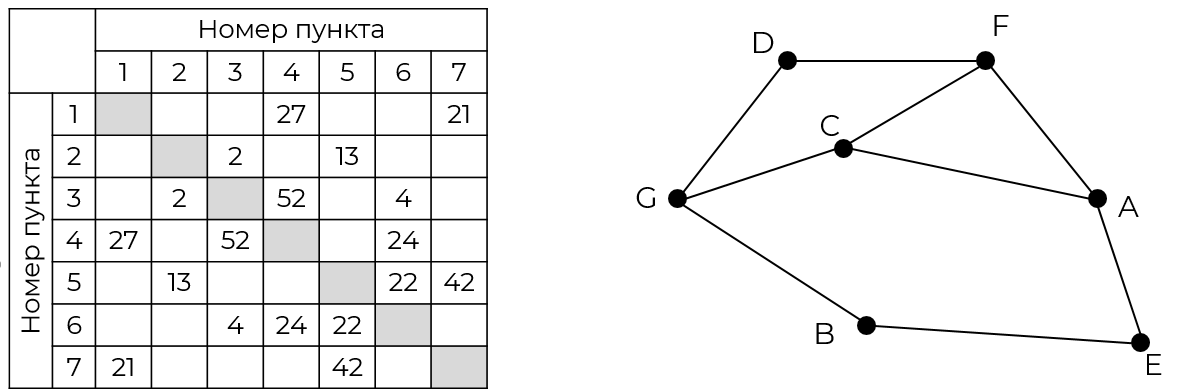
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта А в пункт F и из F в пункт D. В ответе запишите число.
Решение
Населённые пункты А, С, F и G имеют по 3 дороги, но пункт С единственный, который соединён с 3 другими пунктами по 3 дороги. Поэтому можно начать определение пунктов именно с С. С другой стороны, пункт G единственный, у кого есть соединения с двумя пунктами по 2 дороги. А пункт D единственный, кто имея 2 дороги, соединён с пунктами у кого по 3 дороги.
Задача 18
На рисунке изображена схема дорог между поселками в виде графа, а в таблице содержится информация о протяженности дорог между поселками.
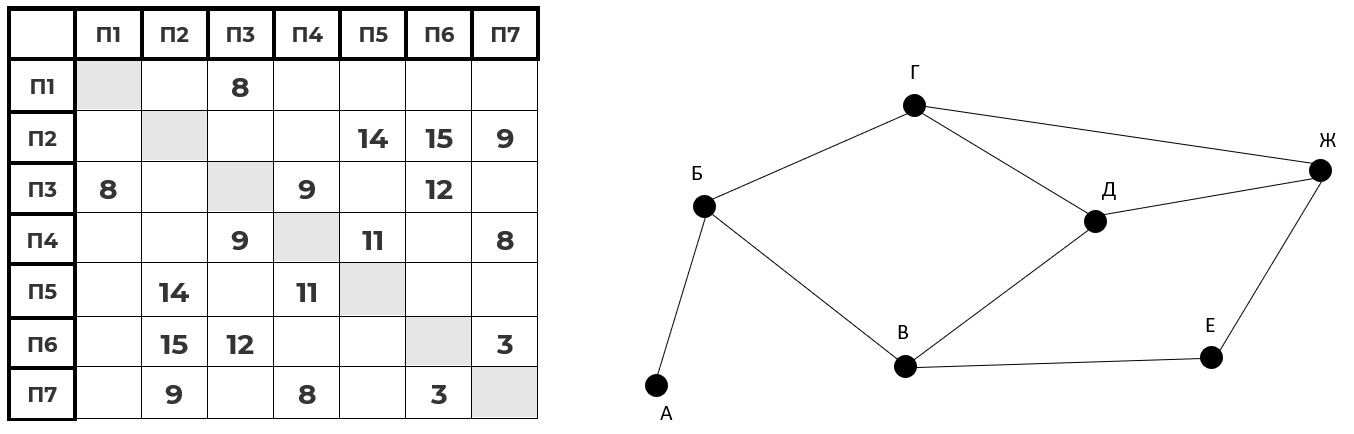
Так как и таблицу, и схему составляли независимо друг от друга, то буквенные обозначения поселков на схеме никак не связаны с их нумерацией в таблице. Определите кратчайший путь из пункта А в пункт Ж. В ответе запишите целое число, означающее протяжённость пути.
Решение
Для начала нужно посчитать количество рёбер для таблицы и графа. После этого соотнести полученные результаты и найти все необходимые данные.
- У нас есть уникальный город (А), с ним связано всего одно ребро, потому его легко сопоставить с таблицей - П1.
- Из города А идёт дорога в Б, в таблице из П1 дорога ведёт в П3, то есть Б = П3.
- У нас есть ещё один особенный город - Е, у него всего две дороги, в таблице это П5.
- В найдём как "общего соседа" для П3 и П5, это П4 (город В)
- Проставим оставшиеся города: Г = П6, Д = П7, Ж = П2
- Нужно просчитать длины всех возможных путей и выбрать наименьший из них:, А - Б - Г - Ж = 8 + 12 + 15 = 35, А - Б - Г - Д - Ж = 8 + 12 + 3 + 9 = 32, А - Б - В - Д - Ж = 8 + 9 + 8 + 9 = 34, А - Б - В - Е - Ж = 8 + 9 + 11 + 14 = 42, А - Б - В - Д - Г - Ж = 8 + 9 + 8 + 3 + 15 = 43
Ответ: 32
Задача 19
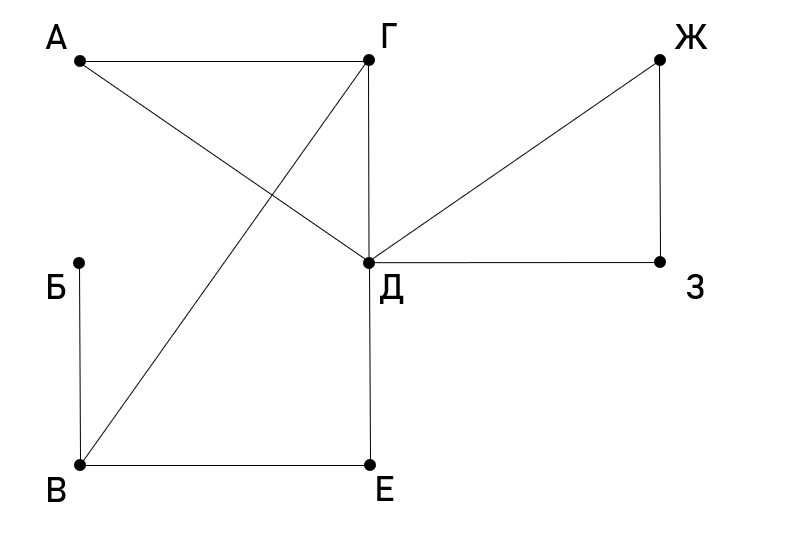
На рисунке изображена схема дорог между поселками в виде графа, а в таблице содержится информация о дорогах между поселками.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | * | * | ||||||
| 2 | * | * | ||||||
| 3 | * | * | * | * | * | |||
| 4 | * | * | ||||||
| 5 | * | |||||||
| 6 | * | * | * | |||||
| 7 | * | * | ||||||
| 8 | * | * | * | |||||
Так как и таблицу, и схему составляли независимо друг от друга, то буквенные обозначения поселков на схеме никак не связаны с их нумерацией в таблице. Определите порядковые номера Ж и З. В ответе укажите комбинацию цифр в порядке возрастания.
Решение
Поселок Б - единственный имеет 1 выезд, его номер - 5. Поселок В - единственный поселок связанный с Б, его номер - 8. Поселок Д - единственный имеет 5 выездов, его номер - 3. Поселок Е связан только с Д и В, его номер - 1. Поселок Г связан с Д и В и имеет 3 выезда, его номер - 6, а поселок А связан только с Д и Г, его номер - 2. Ж и З - оставшиеся поселки, имеют номера 4 и 7.
Ответ:47.
Задача 20
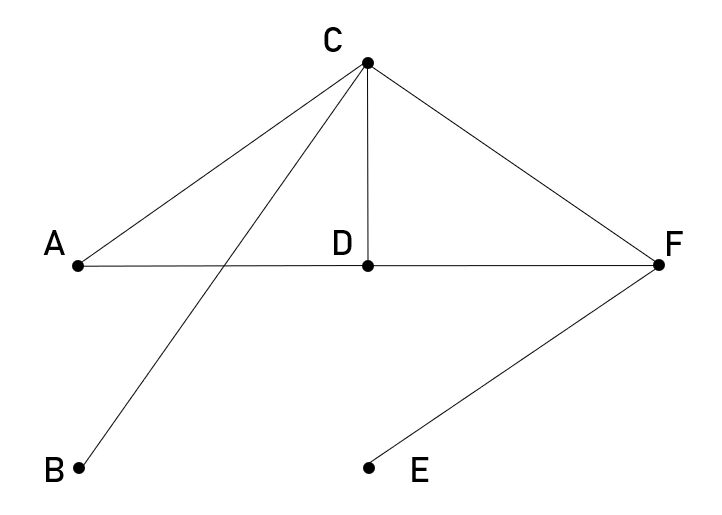
На рисунке изображена схема дорог между поселками в виде графа, а в таблице содержится информация о протяженности дорог между поселками.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 17 | 7 | 8 | 4 | ||
| 2 | 17 | 11 | ||||
| 3 | 7 | 5 | 14 | |||
| 4 | 5 | |||||
| 5 | 8 | |||||
| 6 | 4 | 11 | 14 |
Так как и таблицу, и схему составляли независимо друг от друга, то буквенные обозначения поселков на схеме никак не связаны с их нумерацией в таблице. Определите протяженность кратчайшего пути между поселками E и A. В ответе укажите целое число, обозначающее длину дороги.
Решение
Поселок C - единственный имеет 4 выезда, его номер - 1. Поселок B - единственный имеет 1 выезд и при этом связан с С, его номер - 5. Поселок E - единственный из оставшихся имеет 1 выезд, его номер - 4. Поселок F - единственный из оставшихся связан с Е, его номер - 3. Поселок А - единственный имеет 2 выезда, его номер - 2. Оставшимся поселком является D, его номер - 6.
Зная номера каждого поселка, перебираем все возможные пути из Е в А:
E-F-D-A=30
E-F-C-A=29
E-F-C-D-A=27
Ответ:27.
Рекомендуемые курсы подготовки

- Узнаешь как кодируется изображение
- Поймешь как решать 7 номер ЕГЭ
- Разберешься с паролями
- Потренируешь 11 и 4 номер ЕГЭ
на бесплатном курсе Турбо ЕГЭ

